给n<=50000个longlong范围内的可正可负的数字问下面式子的最大值:
$f(l,r)=(a_l,a_{l+1},...,a_{r-1},a_r)(\sum_{i=l}^{r}a_i-max(a_l,a_{l+1},...,a_{r-1},a_r))$。
注意到括号里那坨区间和-区间最大值在区间gcd不变的前提下是区间越大越好的。才怪嘞,有负数。
枚举右端点,注意到从这里往左走gcd会下降最多log次,而且随着右端点往右移动,这些下降的地点会不递减,因此暴力平移这些下降的地点复杂度是$O(nlog_2Max)$的。
然后就需要询问:一些以某处为右端点的区间的最大的$(\sum_{i=l}^{r}a_i-max(a_l,a_{l+1},...,a_{r-1},a_r))$。由于是枚举右端点,那看看加进这个数字之后这些东西会怎么变。
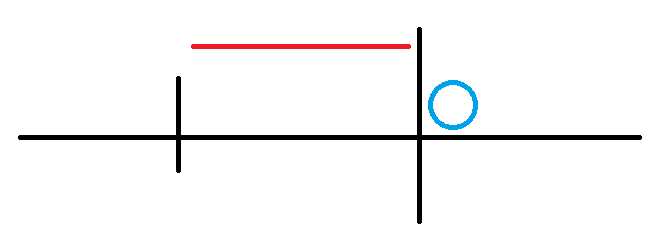
比如说要加进这个蓝色的东西,现在要看所有以蓝色点为右端点的区间和-Max的最大值怎么变。这条线里面每一个数字表示以这里为左端点,蓝色点为右端点的区间的区间和-Max的最大值。首先有一部分数字的最大值是会变化的,就看成红色的那部分。红色那部分左边剩下的部分最大值不变,可以直接区间+蓝色点数值。红色部分会先加上这区间原本的Max,然后加上蓝色点数值,然后再减去蓝色点数值,也就是加上了原本Max。而区间加、维护原数字区间Max和维护这些(区间和-Max)的最大值的最大值都可以线段树搞定。完。
