源: 线性代数的本质
1、线性组合(linear combination)
So any time that you‘re scaling two vectors and adding them like this, it‘s called a linear combination of those two vectors.
2、张成空间(span)
“缩放向量并且相加”这一概念至关重要
所有可以表示为给定向量线性组合的向量的集合
被称为给定向量张成的空间(span)
两个向量张成的空间实际上是问
仅通过向量加法与向量数乘这两种基础运算
你能获得的所有可能向量的集合是什么
如何进行几何想象
当你只考虑一个向量时,就把它看作箭头
当你考虑多个向量时,就把它们都看作点(将每个向量抽象为它的终点)
两个不共线向量张成二维空间,三个不共面向量张成三维空间。
3、线性无关(linearly independent)
不论是张成空间还是线性相关、线性无关都是基于一组向量而言的!
我们说一组向量线性相关,意思就是这组向量中存在多余的向量,
什么是多余的向量呢?就是“对张成空间没有贡献的向量”,
所谓的没有贡献是指不论有没有“你(那个向量)”,张成的集合都不会变。
4、基(basis vectors)
What this means, basically, is that when you think about coordinates as scalars, the basis vectors are what those scalars actually, you know, scale.
空间的一组基的严格定义是这样的:张成该空间的一个线性无关向量的集合。
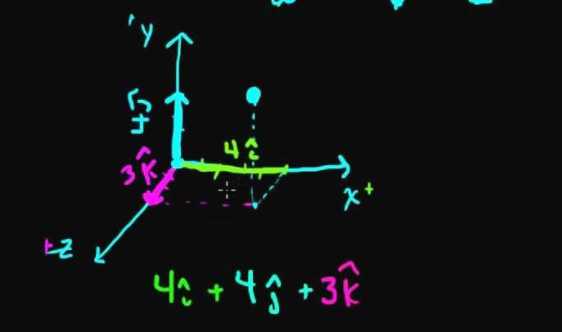
i-hat 和 j-hat 、k-hat (x. y. z 方向上的单位向量)是我们最熟悉的一个基。
5、在数字与向量之间转化
每当我们用数字描述向量时,它都依赖于我们正在使用的基
例如说对于向量 (3, 5) 它并不能直接映射成一个确切的向量,它具体长什么样取决于我们所建立的基。
