源: 线性代数的本质
To ask the right question is harder than to answer it. -Georg Cantor
印象中,我在视频里曾看到过这样的两句话(没有经过核实),其中一句是“向量是线性变换的载体”,另外一句是“当线性变换作用于空间······”。
之后我一直有一种误解:向量是一种“物质”,而运动变化(线性变换)必然是作用于物质之上的,不应该有脱离向量的线性变换。这种观点给我理解概念带来了一些困扰。
例如说,我反复看了好几遍才明白“列空间(column space)”到底是在说什么。
因为在我原本的理解中,只存在 A x = y 这种式子,意思就是矩阵 A 作用于向量 x 得到向量 y 。而实际上单独一个 A 就已经表示了一个线性变换的全过程。我们可以这样理解: A 描述了两个空间状态,一个是原始的空间状态 E (维数和矩阵列数相同),另外一个则是变换后的空间状态 A (维数可能小于等于矩阵列数),而变换后的空间状态 A 就被称作列空间,亦即由变换后的基仅通过向量加法与向量数乘这两种基础运算,所能获得的所有可能向量的集合。
另外一个很重要的观点是:不论是 A 、x 还是 y 都只是在一个默认基下对线性变换的描述罢了。如果想不明白,可以脑补一个3D模型,然后考虑如何用计算机来处理它。
1、秩(rank)
列空间的维度数。
2、逆矩阵(Inverse matrices)
这不仅仅是将方程组写进一行的书写技巧,它还阐明了这个问题中优美的几何直观部分,矩阵A代表一种线性变换,所以求解Ax=v意味着我们去寻找一个向量x,使得它在变换后与v重合,思考一下这一过程,你完全可以只考虑对空间变形,以及变换前后向量的重叠,就将多个未知量相互混合的复杂方程组印入脑中,很酷,对吧?
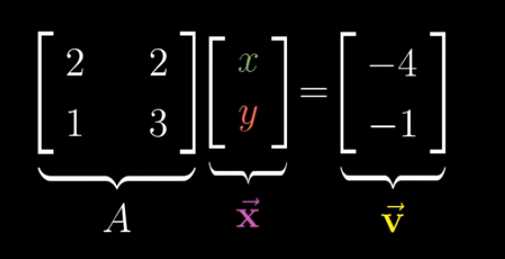
现在,这个方程的解依赖于矩阵A所代表的变换,是将空间挤压到一条线或一个点等低维空间,还是保持像初始状态一样的完整二维空间,用上期视频中的语言来说,我们将它们分为两种情况:A的行列式为零和A的行列式不为零,先来看看最可能发生的情况,即A的行列式不为零,此时空间并未被挤压为零面积的区域,在这种情况下,有且仅有一个向量(在变换后)与v重合,并且你可以通过逆向进行变换来找到这个向量,如同倒带一样,通过跟踪v的动向,你就能找到满足Ax=v的向量x,当你逆向进行变换时,它实际上对应了另一个线性变换,通常被称为“A的逆”,记为A^(-1)
所以A逆的核心性质在于
A逆乘以A等于一个“什么都不做”的矩阵
随机选一个矩阵,有很大可能会遇到这一非零行列式的情况
也就是说,对于两个未知量和两个方程构成的方程组
几乎可以确定它存在唯一解
3、零空间(null space)

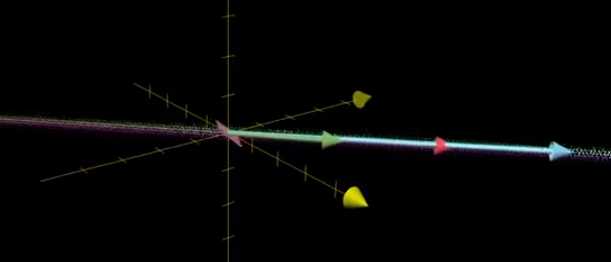
如果一个三维线性变换将空间压缩到一条直线上,那么就有一整个平面上的向量在变换后落在原点,变换后落在原点的向量的集合,被称为矩阵的“零空间”或“核”,变换后一些向量落在零向量上,而“零空间”正是这些向量所构成的空间,对线性方程组来说,当向量v恰好为零向量时,零空间给出的就是这个向量方程所有可能的解
以上就是从几何角度理解线性方程组的一个高水平概述,每个方程组都有一个线性变换与之联系,当逆变换存在时,你就能用这个逆变换求解方程组,否则,列空间的概念让我们清楚什么时候存在解,零空间的概念有助于我们理解所有可能的解的集合是什么样的
