作者:桂。
时间:2018-01-06 14:00:25
链接:http://www.cnblogs.com/xingshansi/p/8214122.html
前言
对于数字接收来讲,射频域随着带宽的增加,AD、微波、FPGA资源的需求越来越高,但频域开的越宽并不意味着频谱越宽,有限信号内可认为信号在宽开频域稀疏分布,最近较为流行的稀疏FFT(SFFT)是在传统FFT的基础上,利用了信号的稀疏特性,使得计算性能优于FFT。本文简单记录自己的理解。
一、稀疏FFT
主要是12年MIT的论文:Simple and Practical Algorithm for Sparse Fourier Transform。
核心思想:
SFT 作为这样一种“输出感知”算法,其核心思路是按照一定规则 Γ ( • )将信号频点投入到一组“筐”中(数量为 B,通过滤波器实现 ) . 因频域是稀疏的,各大值点将依很高的概率在各自的“筐”中孤立存在 . 将各“筐”中频点叠加,使 N 点长序列转换为 B点的短序列并作 FFT 运算,根据计算结果,忽略所有不含大值点的“筐”,最后根据对应分“筐”规则,设计重构算法 Γ -1 ( • )恢复出 N 点原始信号频谱。
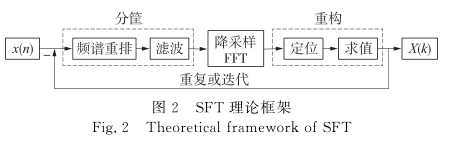
算法流程:

步骤一:选定一个sigma,实现数据频域重排。
频域重排主要是因为FFT之后,频域大值集中在一起,需要将这一伙打散,保证频域的稀疏性(sparse)。sigma的选择主要利用性质:
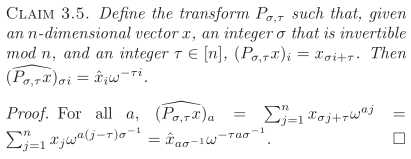
这里sigma^-1是sigma关于模N的逆元。该点主要说明:变化前后的完备性(信号可重建)。
步骤二:加窗。
这里根据筐的多少(B),平分2pi频域,即带宽2pi/B,理想窗函数为矩形窗,但时域为无限长的sinc函数,需要加窗截断,可选择gausswin。
即win = sinc.*gausswin。
步骤三:频域抽取并作FFT
加窗之后,保证了频谱不至于展宽严重,进一步保证了稀疏性。频域降采样:
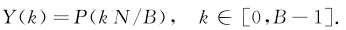
等价于时域的混叠的傅里叶变换:
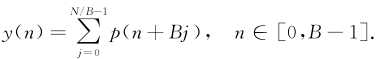
故直接在时域进行处理。处理完成后进行FFT运算。
该操作的理论基础为:

步骤四:哈希映射
主要就是(4)~(6)的操作,这个就比较直观了。
code(仅供参考)
clc;clear all;close all;
%%*************Step0:生成信号**************
fs = 1000;
f0 = 100;
N = 256*256;
t = [0:N-1]/fs;
x = exp(1j*2*pi*t*f0);
%%*************Step1:频谱随机重排**************
sigma = 19; %inv(sigma) = 27
pn = [];
for i = 1:sigma
data = x(i:sigma:end);
pn = [pn data];
end
%%*************Step2:加窗**************
%加窗函数,窗函数频谱宽度与B的尺寸有关,宽度理论上为2*pi/B
%此处B取32
B = 32*32;
n0 = -N/2:N/2-1;
G = sinc(pi/B*n0).*gausswin(N)‘;%2*pi/B
%滤波
pn = pn.*G;
% figure()
% plot(abs(fft(G)));
%%*************Step3:FFT降采样**************
%降采样序列
yn = sum(reshape(pn,B,N/B),2);
figure()
plot(abs(fft(yn)));
%%*************Step4:频率估计**************
%根据Hash映射
[val,hk] = max(abs(fft(yn)));
k_est = round(hk*N/sigma/B);
% omega_k = sigma*k-hk*(N/B);
[~,k_real] = max(abs(fft(x)));
disp([k_real k_est])
