SLAM入门之视觉里程计(4)：基础矩阵的估计

在上篇文章中，介绍了三位场景中的同一个三维点在不同视角下的像点存在着一种约束关系：对极约束，基础矩阵是这种约束关系的代数表示，并且这种约束关系独立与场景的结构，只依赖与相机的内参和外参（相对位姿）。这样可以通过通过匹配的像点对计算出两幅图像的基础矩阵，然后分解基础矩阵得到相机的相对位姿。

通过匹配点对估算基础矩阵

基础矩阵表示的是图像中的像点\(p_1\)到另一幅图像对极线\(l_2\)的映射，有如下公式：
\[ l_2 = Fp_1 \]
而和像点\(P_1\)匹配的另一个像点\(p_2\)必定在对极线\(l_2\)上，所以就有：
\[ p_2^Tl_2 = p_2^TFp_1 = 0 \]
这样仅通过匹配的点对，就可以计算出两视图的基础矩阵\(F\)。
基础矩阵\(F\)是一个\(3\times3\)的矩阵，有9个未知元素。然而，上面的公式中使用的齐次坐标，齐次坐标在相差一个常数因子下是相等，\(F\)也就只有8个未知元素，也就是说，只需要8对匹配的点对就可以求解出两视图的基础矩阵\(F\)。下面介绍下8点法 Eight-Point-Algorithm计算基础矩阵的过程。

假设一对匹配的像点\(p_1=[u_1,v_1,1]^T,p_2=[u_2,v_2,1]^T\)，带入式子中，得到：
\[ [u_1,v_1,1]\left[\begin{array}{ccc}f_1&f_2&f_3\\f_4&f_5&f_6\\f_7&f_8&f_9\end{array}\right] \left[\begin{array}{c}u_2\\v_2\\1\end{array}\right] = 0 \]
把基础矩阵\(F\)的各个元素当作一个向量处理
\[ f = [f_1,f_2,f_3,f_4,f_5,f_6,f_7,f_8,f_9] \]
那么上面式子可以写为
\[ [u_1u_2,u_1v_2,u_1,v_1u_2,v_1v_2,v_1,u_2,v_2,1]\cdot f = 0 \]
对于其他的点对也使用同样的表示方法。这样将得到的所有方程放到一起，得到一个线性方程组(\((u^i,v^i)\)表示第\(i\)个特征点）
\[ \left[ \begin{array}{ccccccccc} u_1^1u_2^1&u_1^1v_2^1&u_1^1&v_1^1u_2^1&v_1^1v_2^1&v_1^1&u_2^1&v_2^1&1\u_1^2u_2^2&u_1^2v_2^2&u_1^2&v_1^2u_2^2&v_1^2v_2^2&v_1^2&u_2^2&v_2^2&1\u_1^3u_2^3&u_1^3v_2^3&u_1^3&v_1^3u_2^1&v_1^3v_2^1&v_1^3&u_2^3&v_2^3&1\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots&\cdots \u_1^8u_2^8&u_1^8v_2^8&u_1^8&v_1^8u_2^8&v_1^8v_2^8&v_1^8&u_2^8&v_2^8&1 \end{array} \right] \left[ \begin{array}{c} f_1\\f_2\\f_3\\f_4\\f_5\\f_6\\f_7\\f_8\\f_9 \end{array} \right]=0 \]
求解上面的方程组就可以得到基础矩阵各个元素了。当然这只是理想中的情况，由于噪声、数值的舍入误差和错误的匹配点的影响，仅仅求解上面的线性方程组得到的基础矩阵非常的不稳定，因此在8点法的基础上有各种改进方法。

图像坐标归一化 Normalizing transformation

将上面公式中由匹配的点对坐标组成的矩阵记为系数矩阵\(A\)
\[ Af = 0 \]
系数矩阵\(A\)是利用8点法求基础矩阵的关键，所以Hartey就认为，利用8点法求基础矩阵不稳定的一个主要原因就是原始的图像像点坐标组成的系数矩阵\(A\)不好造成的，而造成\(A\)不好的原因是像点的齐次坐标各个分量的数量级相差太大。基于这个原因，Hartey提出一种改进的8点法，在应用8点法求基础矩阵之前，先对像点坐标进行归一化处理，即对原始的图像坐标做同向性变换，这样就可以减少噪声的干扰，大大的提高8点法的精度。

预先对图像坐标进行归一化有以下好处：

• 能够提高运算结果的精度
• 利用归一化处理后的图像坐标，对任何尺度缩放和原点的选择是不变的。归一化步骤预先为图像坐标选择了一个标准的坐标系中，消除了坐标变换对结果的影响。

归一化操作分两步进行，首先对每幅图像中的坐标进行平移（每幅图像的平移不同）使图像中匹配的点组成的点集的形心（Centroid）移动到原点；接着对坐标系进行缩放是的点\(p=(x,y,w)^T\)中的各个分量总体上有一样的平均值，各个坐标轴的缩放相同的，最后选择合适的缩放因子使点\(p\)到原点的平均距离是\(\sqrt{2}\)。 概括起来变换过程如下：

1. 对点进行平移使其形心位于原点。
2. 对点进行缩放，使它们到原点的平均距离为\(\sqrt{2}\)
3. 对两幅图像独立进行上述变换

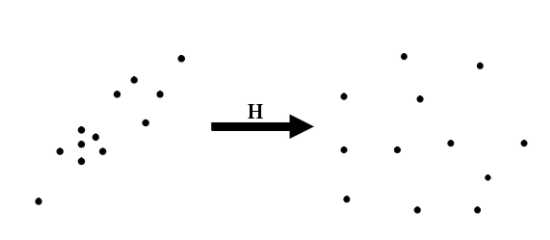
上图左边是原始图像的坐标，右边是归一化后的坐标，\(H\)是归一化的变换矩阵，可记为如下形式：
\[ H = S\left[\begin{array}{ccc} 1&0&-\bar{\mu} \\0&1&-\bar{\nu}\\0&0&\frac{1}{S} \end{array}\right] \]
其中，\(\bar{\mu},\bar{\nu}\)是图像像点坐标两个分量的平均值
\[ \bar{\mu} = \frac{1}{N}\sum_{i=1}^{N}\mu_i,\bar{\nu} = \frac{1}{N}\sum_{i=1}^{N}\nu_i \]
\(S\)表示尺度，其表达式为：
\[ S = \frac{\sqrt{2\cdot N}}{\sqrt{\sum_{i=1}^{N}(\mu_i-\bar{\mu})^2 + (\nu_i-\bar{\nu})^2}} \]

这样，首先对原始的图像坐标进行归一化处理，再利用8点法求解基础矩阵，最后将求得的结果解除归一化，得到基础矩阵\(F\)，总结如下：

1. 对图像1进行归一化处理，计算一个只包含平移和缩放的变换\(H_1\)，将图像1中的匹配点集\({p_i^1}\)变换到新的点集\(\hat{p_i^1}\)，新点集的形心位于原点\((0,0)^T\)，并且它们到原点的平均距离是\(\sqrt{2}\)。
2. 对图像2，计算变换矩阵\(H_2\)进行相同的归一化处理
3. 使用8点法利用变换后的点集估计基础矩阵\(\hat{F}\)
4. 根据变换\(F = H_2^T\hat{F}H_1\)

使用归一化的坐标虽然能够在一定程度上消除噪声、错误匹配带来的影响，但还是不够的。

最小二乘法

仅仅对图像坐标进行归一化处理，能在一定程度上提高计算的精度，但在实践中还是不够的。8点法中，只使用8对匹配的点对估计基础矩阵，但通常两幅图像的匹配的点对远远多于8对，可以利用更多匹配的点对来求解上面的方程。
由于基础矩阵\(F\)在一个常量因子下是等价的，这样可以给基础矩阵\(F\)的元素组成的向量\(f\)施加一个约束条件
\[ \parallel f \parallel = 1 \]
这样由\(K \ge 8\)个匹配的点对，组合成一个矩阵\(Q_{K\times9}\)，求解上面方程就变成了求解如下问题的最小二乘解
\[ \min_{\parallel f \parallel = 1}\parallel Qf \parallel ^2 \]
其中，矩阵\(Q\)的每一行来自一对匹配点；\(f\)是基础矩阵\(F\)元素构成的待求解的向量，根据2-范数的定义
\[ \parallel Qf \parallel^2 = (Qf)^T(Qf)=f^T(Q^TQ)f \]
将上式的中间部分提取出来得到矩阵\(M=Q^TQ\),这是一个\(9\times9\)的矩阵。基于拉格朗日-欧拉乘数优化定理，在\(\parallel f \parallel = 1\)约束下，\(Qf=0\)的最小二乘解，为矩阵\(M=Q^TQ\)的最小特征值对应的特征向量。所以可以对矩阵\(Q\)进行奇异值分解（SVD）
\[Q = U\Sigma V^T\]
其中，\(Q\)是\(K\times9\)的矩阵；\(U\)是\(K\times K\)的正交阵；\(\Sigma\)是\(K \times 9\)的对角矩阵，对角线的元素是奇异值；\(V^T\)是\(9 \times 9\)的正交阵，每一个列向量对应着\(\Sigma\)中的奇异值。所以，最小二乘解就是\(V^T\)的第9个列向量，也就是可由向量\(f=V_9\)构造基础矩阵\(F\)。
基础矩阵\(F\)还有一个重要的性质，这里可以作为进一步的约束条件。那就是基础矩阵\(F\)的秩为2，
\[ Rank(F) = 2 \]
上述使用列向量\(V_9\)构造的基础矩阵的秩通常不为2，需要进一步的优化。在估计基础矩阵时，设其最小奇异值为0，对上面方法取得的基础矩阵进行SVD分解
\[ F = SVD = S\left[\begin{array}{ccc} v_1&0&0\\0&v_2&0\\0&0&v_3 \end{array}\right]D \]
其最小特征值\(v_3\)被设为0，以使得\(F\)的秩为2.这样得到
\[ F = SVD = S\left[\begin{array}{ccc} v_1&0&0\\0&v_2&0\\0&0&0 \end{array}\right]D \]
上述\(F\)就是最终得到的基础矩阵。

对上面进行总结，使用最小二乘法估算基础矩阵的步骤如下：

1. 对取得两幅图像的匹配点进行归一化处理，转换矩阵分别是\(H_1,H_2\)
2. 有对应的匹配点(\(K\ge8\))构造系数矩阵\(Q\)
3. 对矩阵\(Q\)进行SVD分解,\(Q=U\Sigma V^T\)，由向量\(f=V_9\)构造矩阵\(\hat{F}\)
4. 对得到的矩阵\(\hat{F}\)进行秩为2的约束，即对\(\hat{F}\)进行SVD分解，\(\hat{F}=S\cdot diag(v_1,v_2,v_3) \cdot V^T\)，令\(v_3=0\)得到基础矩阵的估计\(F'=S\cdot diag(v_1,v_2,0) \cdot V^T\)
5. 对上一步得到的解进行反归一化处理，得到基础矩阵\(F=H_2^TF'H_1\)

随机采样一致性 RANSAC

基于匹配点对估算两视图的基础矩阵，唯一的已知条件就是匹配的点对坐标。在实践中，点对的匹配肯定是存在误差的，主要有两种类型的误差：

1. 不精确的测量点位置引起的系统误差，通常服从高斯分布
2. 错误匹配引起的误差，这些不匹配的点被称为外点，通常不服从高斯分布

对于基础矩阵的估算，不匹配的点能够造成很大的误差，即使是只有一对错误的匹配都能使估算值极大的偏离真实值。因此，需要找到一种方法，从包含错误点（外点）的匹配点对集合中，筛选出正确的匹配点（内点）。

RANSAC(Random Sample Consensus)随机采样一致性从一组含有外点的数据集中，通过迭代的方式估计出符合该数据集的数学模型的参数。因此，它也可以用来检测出数据集中的外点。
RANSAC有两个基本的假设：

• 数据集中包含的内点，内点的分布符合一个数学模型；而数据集中的外点不复合该数学模型
• 能够一组内点（通常很少）集合能够估计出其符合的数据模型

RANSAC的具体思想是：给定\(N\)个数据点组成的集合\(P\)，假设集合中大多数的点都是可以通过一个模型来产生的，且最少通过\(n\)个点可以拟合出模型的参数，则可以通过以下的迭代方式拟合该参数：

1. 从集合\(P\)中随机选择\(n\)个点
2. 使用这\(n\)个点估计出一个模型\(M\)
3. 对\(P\)中剩余的点，计算每个点与模型\(M\)的距离，距离超过阈值则认为是外点；不超过阈值则认为是内点，并记录该模型\(M\)所对应的内点的个数\(m_i\)

将上面步骤重复\(k\)次，选择最大\(m_i\)所对应的模型\(M\)作为最终结果。
在迭代次数\(k\)的选择是一个关键，可以通过理论的方式计算出\(k\)的取值。在选择\(n\)个点估计模型时，要保证选择的\(n\)的个点都是内点的概率足够的高。假设，从数据集中选择一个点为内点的概率为\(\varpi\)，则选择的\(n\)个点都是内点的概率为\(\varpi^n\);则\(1-\varpi^n\)表示选择的\(n\)个点至少有一个是外点，用包含外点估算的模型显然是不正确的，则迭代\(k\)次均得不到正确模型的概率为\((1-\varpi^n)^k\)。设\(p\)表示\(k\)次迭代中至少有一次选择的点都是内点的概率，也就是估计出了正确的模型，则\(1-p\)就表示\(k\)次跌点都得到正确的模型，所以有
\[ 1-p = 1-\varpi^n)^k \]
两边同时取对数，则有
\[ k = \frac{log(1-p)}{log(1-\varpi^n)} \]
一般要求\(p\)大于95%即可。

使用RANSAC估算基础矩阵时，首先需要确定判断点是内点还是外点的依据。通过上一篇的两视图的对极几何可知，像点总是在对极线，因此可以选择像点到对极线的距离作为判断该点是内点还是外点的依据，设点到对极的距离的阈值为\(d\)。则使用RANSAC的方法估算基础矩阵的步骤：

• 从匹配的点对中选择8个点，使用8点法估算出基础矩阵\(F_i\)
• 计算其余的点对到其对应对极线的距离\(d_n\)，如果\(d_n\le d\)则该点为内点，否则为外点。记下符合该条件的内点的个数为\(m_i\)
• 迭代k次，或者某次得到内点的数目\(m_i\)占有的比例大于等于95%，则停止。选择\(m_i\)最大的基础矩阵作为最终的结果。

RANSAC能够不依赖于任何额外信息的情况下，将数据划分为内点和外点。但也有其相应的缺点，RANSAC并不能保证得到正确的结果，需要提高迭代的次数；另一个是，内点外点的判断需要设置阈值。

OpenCV 计算基础矩阵

上面写了那么多基础矩阵的计算方法，在OpenCV中也就是一个函数的封装

Mat cv::findFundamentalMat(InputArray points1,
InputArray     points2,
int     method = FM_RANSAC,
double     param1 = 3.,
double     param2 = 0.99,
OutputArray     mask = noArray() 
)

其中，points1,points2是匹配点对的像素坐标，并且能够一一对应。method表是使用那种方法，默认的是FM_RANSAC也就是RANSAC的方法估算基础矩阵。param1表示RANSAC迭代过程中，判断点是内点还是外点的阈值（到对极线的像素距离）；param2表示内点占的比例，以此来判断估计出的基础矩阵是否正确。

//////////////////////////////////////////////////////
    // 
    // 利用已经匹配的点对，使用RANSAC的方法，估计两视图的基础矩阵
    //
    //////////////////////////////////////////////////////
    
    // 1. 对齐匹配的点对
    vector<KeyPoint> alignedKps1, alignedKps2;
    for (auto i = 0; i < good_matches.size(); i++)
    {
        alignedKps1.push_back(keypoints1[good_matches[i].queryIdx]);
        alignedKps2.push_back(keypoints2[good_matches[i].trainIdx]);
    }
    // 2. 取得特征点的像素坐标
    vector<Point2f> ps1, ps2;
    for (auto i = 0; i < alignedKps1.size(); i++)
    {
        ps1.push_back(alignedKps1[i].pt);
        ps2.push_back(alignedKps2[i].pt);
    }
    // 3. RANSAC 计算基础矩阵F
    Mat F;
    F = findFundamentalMat(ps1, ps2, FM_RANSAC);
    cout << "基础矩阵F:" << endl << F << endl;

首先需要将匹配的点对放在两个数组中，并且一一对应（匹配的点在两个数组中的下标是一样的），然后再取得匹配点的像素坐标，最后调用findFundamentalMat使用RANSAC方法估计基础矩阵。

通过两视图的对极几何可知，所有的对极线相交于对极点，可以以此来验证估计的基础矩阵是否正确。在OpenCV中也封装了计算对极线的方法computeCorrespondEpilines，

vector<Vec3f> linesl;
    computeCorrespondEpilines(ps1, 1, F, linesl);

    for (auto it = linesl.begin(); it != linesl.end(); it++)
    {
        line(img1, Point(0, -(*it)[2] / (*it)[1]), Point(img1.cols, -((*it)[2] + (*it)[0] * img1.cols) / (*it)[1]), Scalar(255, 255, 255));
    }
    imshow("第一幅图像的对极线", img1);

    vector<Vec3f> lines2;
    computeCorrespondEpilines(ps2, 2, F, lines2);
    for (auto it = lines2.begin(); it != lines2.end(); it++)
    {
        line(img2, Point(0, -(*it)[2] / (*it)[1]), Point(img2.cols, -((*it)[2] + (*it)[0] * img2.cols) / (*it)[1]), Scalar(255, 255, 255));
    }
    imshow("第二幅图像的对极线", img2);

上面代码执行的结果如下：

可以看出所有的对极线都相交于一点，该点就是对极点。