标签:des style blog http color io os 使用 ar
在计算机科学中,堆(Heap)是一种基于树(Tree)的特殊的数据结构。堆需要满足堆特性(Heap Property):如果节点 A 是节点 B 的父节点,则节点 A 中的键值与节点 B 中的键值的比较顺序关系将适用于堆中的所有节点。也就是可以总结为两种情况。
由于堆中的最大值或最小值总是被存储在根节点(Root Node)中,所以名字称为堆。堆不是一种排序的数据结构,可认为是部分排序的结构。从堆的图形结构来看,在相同层级中的节点间没有任何特定的关系,即使是兄弟节点。
堆经常被应用于优先队列(Priority Queue),当你需要找到队列中最高优先级或者最低优先级的元素时,使用堆结构可以帮助你快速的定位元素。
常见的堆实现为二叉堆(Binary Heap),其实际上是一颗二叉树(Binary Tree),并且是一颗完全二叉树(Complete Binary Tree)。如下图中展示了一个完全二叉的最大堆。
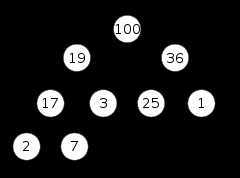
当堆被实现为完全二叉树时,其高度为最小高度。如果堆中有 n 个节点,则最小高度为 Θ(lg n)。
实现堆结构时通常使用数组结构(Array),并且元素间不需要指针引用。使用完全二叉树或者满二叉树实现堆时可以保持最优的空间效率。通常第一个元素或最后一个元素将保存根节点,根节点后紧跟着其两个子节点,两个子节点后将紧跟着 4 个这两个子节点的子节点,以此类推。因此,在一个以 0 为起点的数组中,位置 i 处的节点的子节点的位置将位于 2i+1 和 2i+2 处。平衡一个堆的操作将使用元素互换的方式,所以对堆进行排序无需使用额外的空间,堆排序(heapsort)即是用了这种就地排序(In-Place)的方式。
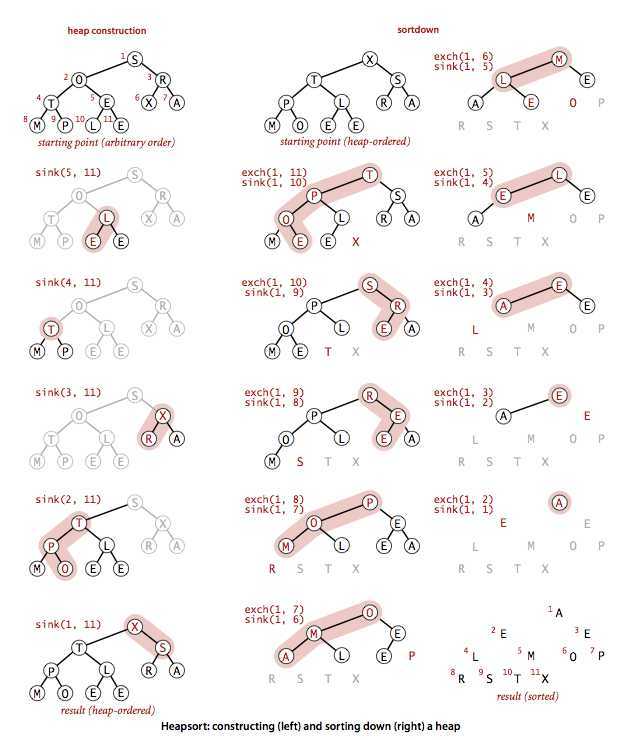
堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。二叉堆数据结构是一种数组对象,它可以被视为一棵完全二叉树。树中每个节点与数组中存放该节点值的那个元素对应。在堆排序算法中,我们使用最大堆。
堆节点的访问
通常堆是通过一维数组来实现的。在数组起始为 0 的情形中,如果 i 为当前节点的索引,则有
堆的操作
在堆的数据结构中,堆中的最大值总是位于根节点。堆中定义以下几种操作:
算法复杂度
1 class Program 2 { 3 static void Main(string[] args) 4 { 5 int[] unsorted = { 4, 9, 5, 2, 6, 3, 7, 1, 8 }; 6 7 HeapSortByMaxHeap(unsorted); 8 9 foreach (var key in unsorted) 10 { 11 Console.Write("{0} ", key); 12 } 13 14 Console.Read(); 15 } 16 17 static void HeapSortByMaxHeap(int[] unsorted) 18 { 19 // build the heap in array so that largest value is at the root 20 BuildMaxHeap(unsorted); 21 22 // swap root node and the last heap node 23 for (int i = unsorted.Length - 1; i >= 1; i--) 24 { 25 // array[0] is the root and largest value. 26 // the swap moves it in front of the sorted elements 27 int max = unsorted[0]; 28 unsorted[0] = unsorted[i]; 29 unsorted[i] = max; // now, the largest one is at the end 30 31 // the swap ruined the heap property, so restore it 32 // the heap size is reduced by one 33 MaxHeapify(unsorted, 0, i - 1); 34 } 35 } 36 37 static void BuildMaxHeap(int[] unsorted) 38 { 39 // put elements of array in heap order, in-place 40 // start is assigned the index in array of the last parent node 41 // the last element in 0-based array is at index count-1; 42 // find the parent of that element 43 for (int i = (unsorted.Length / 2) - 1; i >= 0; i--) 44 { 45 // move a node down in the tree, as long as needed 46 // shift down the node at index start to the proper place 47 // such that all nodes below the start index are in heap order 48 MaxHeapify(unsorted, i, unsorted.Length - 1); 49 } 50 // after shifting down the root all nodes/elements are in heap order 51 } 52 53 static void MaxHeapify(int[] unsorted, int root, int bottom) 54 { 55 int rootValue = unsorted[root]; 56 int left = root * 2 + 1; // start from left child 57 58 // while the root has at least one child 59 while (left <= bottom) 60 { 61 // has more children 62 if (left < bottom) 63 { 64 // if there is a right child and that child is greater 65 if (unsorted[left] < unsorted[left + 1]) 66 { 67 left = left + 1; 68 } 69 } 70 71 // compare root and the older children 72 if (rootValue < unsorted[left]) 73 { 74 // swap 75 unsorted[root] = unsorted[left]; 76 root = left; 77 78 // repeat to continue sifting down the child now 79 left = root * 2 + 1; // continue from left child 80 } 81 else 82 { 83 left = bottom + 1; 84 } 85 } 86 87 unsorted[root] = rootValue; 88 } 89 90 static void HeapSortByMinHeap(int[] unsorted) 91 { 92 BuildMinHeap(unsorted); 93 94 for (int i = unsorted.Length - 1; i >= 1; i--) 95 { 96 int min = unsorted[0]; 97 unsorted[0] = unsorted[i]; 98 unsorted[i] = min; 99 100 MinHeapify(unsorted, 0, i - 1); 101 } 102 103 // reverse 104 for (int i = 0; i < (unsorted.Length / 2); i++) 105 { 106 int t = unsorted[i]; 107 unsorted[i] = unsorted[unsorted.Length - 1 - i]; 108 unsorted[unsorted.Length - 1 - i] = t; 109 } 110 } 111 112 static void BuildMinHeap(int[] unsorted) 113 { 114 for (int i = (unsorted.Length / 2) - 1; i >= 0; i--) 115 { 116 MinHeapify(unsorted, i, unsorted.Length - 1); 117 } 118 } 119 120 static void MinHeapify(int[] unsorted, int root, int bottom) 121 { 122 int rootValue = unsorted[root]; 123 int left = root * 2 + 1; // start from left child 124 125 // while the root has at least one child 126 while (left <= bottom) 127 { 128 // has more children 129 if (left < bottom) 130 { 131 // if there is a right child and that child is smaller 132 if (unsorted[left] > unsorted[left + 1]) 133 { 134 left = left + 1; 135 } 136 } 137 138 // compare root and the older children 139 if (rootValue > unsorted[left]) 140 { 141 // swap 142 unsorted[root] = unsorted[left]; 143 root = left; 144 145 // repeat to continue sifting down the child now 146 left = root * 2 + 1; // continue from left child 147 } 148 else 149 { 150 left = bottom + 1; 151 } 152 } 153 154 unsorted[root] = rootValue; 155 } 156 }
本文《二叉堆》由 Dennis Gao 发表自博客园博客,任何未经作者本人允许的人为或爬虫转载均为耍流氓。
标签:des style blog http color io os 使用 ar
原文地址:http://www.cnblogs.com/gaochundong/p/binary_heap.html