NOIP2017 小凯的疑惑

https://www.luogu.org/problemnew/show/P3951

以a=7，b=3 为例

把自然数按一行a个划分

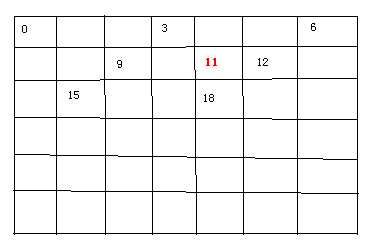
假设现在已有了 ax+by=k   x，y 都是非负整数

假设k在第r行的第h列，

在k的基础上，无论加多少a，新的可以表示的数也一定在第h列

即第h列，自第r行往下的行 所代表的数 都可以用a，b 凑出来

那么我们一个一个的往上加b

0个b：

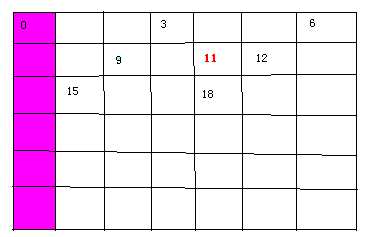
1个b：

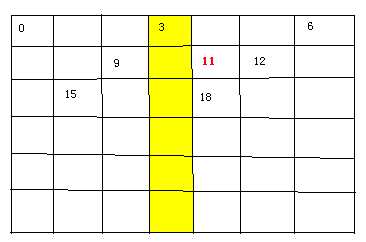
2个b：

……

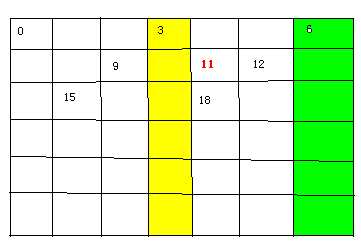
6个b：

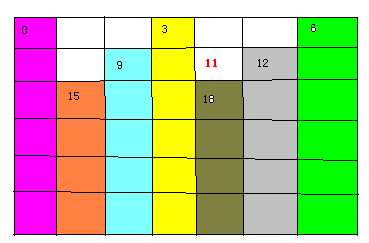
当加到a-1个b时，出现了被完全覆盖的段

原理：

当a，b互质时，{b，2b，3b……（a-1）b} 构成了模b意义下的完全剩余系

（a-1）b 是最后一次覆盖

  那它上面的（a-1）b - a 就是最后一个没有被覆盖的数

#include<iostream>
using namespace std;
int main()
{
    long long a,b;
    cin>>a>>b;
    cout<<a*b-a-b;
}

题目描述

小凯手中有两种面值的金币，两种面值均为正整数且彼此互素。每种金币小凯都有 无数个。在不找零的情况下，仅凭这两种金币，有些物品他是无法准确支付的。现在小 凯想知道在无法准确支付的物品中，最贵的价值是多少金币？注意：输入数据保证存在 小凯无法准确支付的商品。

输入输出格式

输入格式：

输入数据仅一行，包含两个正整数 aa 和 bb，它们之间用一个空格隔开，表示小凯手 中金币的面值。

输出格式：

输出文件仅一行，一个正整数 NN，表示不找零的情况下，小凯用手中的金币不能准确支付的最贵的物品的价值。

输入输出样例

3 7

11

说明

【输入输出样例 1 说明】

小凯手中有面值为3和7的金币无数个，在不找零的前提下无法准确支付价值为1、 2、4、5、8、11 的物品，其中最贵的物品价值为 11，比 11 贵的物品都能买到，比如：

12 = 3 \times 4 + 7 \times 012=3×4+7×0

13 = 3 \times 2 + 7 \times 113=3×2+7×1

14 = 3 \times 0 + 7 \times 214=3×0+7×2

15 = 3 \times 5 + 7 \times 015=3×5+7×0

【数据范围与约定】

对于 30%的数据： 1 \le a,b \le 501≤a,b≤50。

对于 60%的数据： 1 \le a,b \le 10^41≤a,b≤104。

对于 100%的数据：1 \le a,b \le 10^91≤a,b≤109。