http://www.lydsy.com/JudgeOnline/problem.php?id=3529
有一张n*m的数表,其第i行第j列(1 < =i < =n,1 < =j < =m)的数值为能同时整除i和j的所有自然数之和。给定a,计算数表中不大于a的数之和。
20000 组询问 n<=1e5
f(k)表示 k 的 约数和
g(k)表示 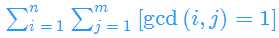
f(k)的求法:
http://www.cnblogs.com/TheRoadToTheGold/p/8228969.html
g(k)的求法:
http://www.cnblogs.com/TheRoadToTheGold/p/6609495.html
假设没有a的限制
不妨令n<=m
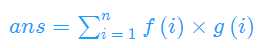
即
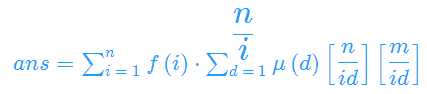
令i*d=t,把后面两个下取整提到前面
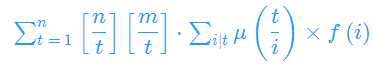
令
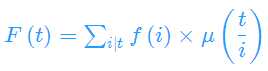
则
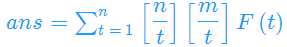
预处理出F(t),除法分块便可以在O(sqrt(n))求解
但是现在有f(i)<=a 的限制
离线处理,读入所有的询问
所以把f(i)按f(i)的值从小到大排序
询问按a的值从小到大排序
用树状数组维护当前F(t)的值
在处理这个询问之前
找出所有<=本次询问a的f(i)
在树状数组中i及i的倍数位置加上f(i)
取模不用管,自然溢出即可
#include<cstdio> #include<iostream> #include<algorithm> using namespace std; #define N 100001 #define M 20001 typedef long long LL; int T; int miu[N]; int p[N]; bool vis[N]; struct nodef { int d,val; }f[N]; int c[N]; bool cmpf(nodef A,nodef B) { if(A.val!=B.val) return A.val<B.val; return A.d<B.d; } struct Query { int id; int n,m,a; }Q[M]; bool cmpQ(Query A,Query B) { return A.a<B.a; } int ans[M]; struct BIT { int s[N]; #define lowbit(x) x&-x void add(int x,int val) { while(x<N-1) { s[x]=s[x]+val; x+=lowbit(x); } } int query(int x) { int sum=0; while(x) { sum=sum+s[x]; x-=lowbit(x); } return sum; } }Bit; void read(int &x) { x=0; int f=1; char c=getchar(); while(!isdigit(c)) { if(c==‘-‘) f=-1; c=getchar(); } while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } x*=f; } void pref() { int cnt=0; miu[1]=1; f[1].d=1; f[1].val=1; for(int i=2;i<N;++i) { f[i].d=i; if(!vis[i]) { p[++cnt]=i; miu[i]=-1; f[i].val=i+1; c[i]=1; } for(int j=1;j<=cnt;++j) { if(i*p[j]>=N) break; vis[i*p[j]]=true; if(i%p[j]==0) { f[i*p[j]].val=f[i].val*p[j]+c[i]; c[i*p[j]]=c[i]; break; } miu[i*p[j]]=-miu[i]; f[i*p[j]].val=f[i].val*(p[j]+1); c[i*p[j]]=f[i].val; } } sort(f+1,f+N,cmpf); } void init() { read(T); for(int i=1;i<=T;++i) { read(Q[i].n); read(Q[i].m); read(Q[i].a); Q[i].id=i; } sort(Q+1,Q+T+1,cmpQ); } void solve() { int nowQ=1; while(Q[nowQ].a<=0) nowQ++; int nowd=1; int j,res; int tot,lastsum,nowsum; for(;nowQ<=T;++nowQ) { while(nowd<N && f[nowd].val<=Q[nowQ].a) { for(int i=f[nowd].d;i<N;i+=f[nowd].d) Bit.add(i,f[nowd].val*miu[i/f[nowd].d]); nowd++; } if(Q[nowQ].n>Q[nowQ].m) swap(Q[nowQ].n,Q[nowQ].m); tot=lastsum=0; for(int i=1;i<=Q[nowQ].n;i=j+1) { j=min(Q[nowQ].n/(Q[nowQ].n/i),Q[nowQ].m/(Q[nowQ].m/i)); nowsum=Bit.query(j); res=nowsum-lastsum; res=res*(Q[nowQ].n/i)*(Q[nowQ].m/i); tot+=res; lastsum=nowsum; } tot+= tot<0 ? 1LL<<31 : 0; ans[Q[nowQ].id]=tot; } for(int i=1;i<=T;++i) cout<<ans[i]<<‘\n‘; } int main() { pref(); init(); solve(); }
