上一篇文章讲了傅立叶变换的本质。这篇文章会总结一下傅立叶变换的常用性质,公式巨多,慎入!慎入!

相关概念
首先,回顾一下傅立叶变换的公式:
\[
F(u)=\frac{1}{M}\sum_{x=0}^{M-1}f(x)e^{-2j\pi (ux/M)}
\]
频谱(spectrum)
由上面的公式可以看出,傅立叶变换得到的系数 \(F(u)\) 是一个复数,因此可以表示为:\(F(u)=R(u)+jI(u)\),其中,\(R(u)\) 是实部,\(I(u)\) 是虚部。傅立叶变换的频谱被定义为:
\[
|F(u)|=\sqrt{R^2(u)+I^2(u)}
\]
相位谱(phase)
根据欧拉公式,我们知道 \(R(u)\) 代表的是一个余弦值,而 \(I(u)\) 则是正弦值。如果把 \(F(u)\) 看作一个向量 \((R(u), I(u))\),则这个向量的夹角为 \(\phi(u)=\arctan{[\frac{I(u)}{R(u)}]}\)。这个夹角也被称为相位谱。
能量谱(power)
能量谱其实就是频谱的平方:\(P(u)=|F(u)|^2=R^2(u)+I^2(u)\)。
常用性质
周期性
所谓周期性,即:
\[
F(u,v)=F(u+M,v)=F(u,v+N)=F(u+M,v+N)
\]
证明如下:
\[
\begin{eqnarray}
F(u+M,v+N)&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi [(u+M)x/M+(v+N)/N]} \&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi [(u+M)x/M+(v+N)y/N]} \&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}e^{-j2\pi (x+y)}
\end{eqnarray}
\]
注意,\(e^{-j2\pi (x+y)}={(e^{-j2\pi})}^{x+y}=1^{(x+y)}=1\),所以
\[
F(u+M,v+N)=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi (ux/M+vy/N)}=F(u,v)
\]
类似地,可以推出
\[
f(x,y)=f(x+M,y)=f(x,y+N)=f(x+M,y+N)
\]
共轭对称性
回忆一下,在复数域中,共轭指的是虚部取反。即 \(z=x+jy\) 的共轭是 \(z*=x-jy\)。
在傅立叶变换中,存在以下共轭对称性:
\[
F(u,v)=F*(-u,-v)
\]
证明如下:
\[
\begin{eqnarray}
F*(-u,-v)&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{ux/M+vy/N} \&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)[\cos{[2\pi (ux/M+vy/N)]}-j\sin{[2\pi(ux/M+vy/N)]}] \text{(注意共轭)} \&=&F(u,v)
\end{eqnarray}
\]
那么这个性质有什么用呢?注意,\(|F*(-u,-v)|=|F(-u,-v)|\),换句话说,\(|F(u,v)|=|F(-u,-v)|\)。
要知道,\(|F(u,v)|\) 表示的是傅立叶频谱图,所以,共轭对称性表明,傅立叶的频谱图是中心对称的。
具体地,下图所示的傅立叶频谱图,四个对角上的能量是沿图片中心对称的。
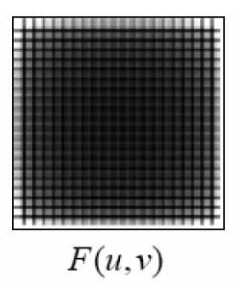
平移性
平移性指的是:
\[
f(x-x_0,y-y_0) \Leftrightarrow F(u,v)e^{-j2\pi (ux_0/M+vy_0/N)} \tag{1}
\]
这个等价关系的意思是说,如果原图 \(f(x,y)\) 平移了 \((x_0,y_0)\) 个单位,那么平移后的图像对应的傅立叶变换为 \(F(u,v)e^{-j2\pi (ux_0/M+vy_0/N)}\),即在原来 \(F(u,v)\) 的基础上乘上 \(e^{-j2\pi (ux_0/M+vy_0/N)}\)。
这个公式的证明很简单。平移前的公式为:
\[
f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi (ux/M+vy/N)}
\]
现在,原图的像素由 \((x,y)\) 平移到 \((x-x_0,y-y_0)\),因此,我们只需要将 \((x-x_0,y-y_0)\) 代入上式即可:
\[
\begin{eqnarray}
f(x-x_0,y-y_0)&=&\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi [(x-x_0)u/M+(y-y_0)v/N]} \&=&\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{-j2\pi(ux_0/M+vy_0/N)}e^{j2\pi (ux/M+vy/N)}
\end{eqnarray}
\]
在保持原来的基底向量不变的情况下,我们只需要将傅立叶系数变成 \(F(u,v)e^{-j2\pi(ux_0/M+vy_0/N)}\) 即可。
同样的,如果频谱图发生平移,有如下关系成立:
\[
F(u-u_0,v-v_0)\Leftrightarrow f(x,y)e^{j2\pi (u_0 x/M+v_0 y/N)} \tag{2}
\]
证明的方法是类似的。
从平移关系中,我们可以得到一个很好的性质。注意,在复数中,有这样两个等式成立 \(|e^{aj}e^{bj}|=|e^{aj}||e^{bj}|\)、\(|e^{jx}|=1\)(不懂的请复习复数相关的内容)。应用到上面的结论,即 \(|F(u,v)e^{-j2\pi (ux_0/M+vy_0/N)}|=|F(u,v)|\)。换句话说,原图平移后,傅立叶频谱图不变。
例如,对于下面两幅图(为了保持图片大小不变,我们在图片外围补了一层 ‘0’ 边界):

它们对应的傅立叶频谱图都是这个样子的:

注意,四个角上的白点代表低频信号的分量。
另外,我们平时经常用的中心化操作也依赖于平移性和周期性。
所谓中心化,就是将频谱图平移 \((M/2, N/2)\) 个单位。由平移性的公式 (2),可以得到:
\[
\begin{eqnarray}
F(u-\frac{M}{2},v-\frac{N}{2}) &\Leftrightarrow& f(x,y)e^{j2\pi (\frac{1}{2}x+\frac{1}{2}y)} \&=&f(x,y)e^{j\pi(x+y)} \&=&f(x,y){e^{j\pi}}^{(x+y)} \&=&f(x,y)(-1)^{x+y}
\end{eqnarray}
\]
所以,我们只要对原图的每个像素乘以 \((-1)^{x+y}\),然后进行傅立叶变换,这样得到的频谱图便是中心化后的频谱图了。
如果对上一幅频谱图中心化,则可以得到:

这么做的目的是为了方便肉眼观察。中心化后,频谱图中心对应的便是低频分量,远离中心的,则是高频分量。
卷积定理
卷积定理表述为:
\[
f(x,y)*h(x,y) \Leftrightarrow F(u,v)H(u,v) \F(u,v)*H(u,v) \Leftrightarrow f(x,y)h(x,y)
\]
(注意,右边式子表示的是矩阵的点乘运算,而不是矩阵乘法)
它的意思是说,在空间域内进行卷积运算,跟把它们转换到频率域再进行点乘运算,效果是等价的。
要证明这个定理,首先要知道卷积的定义(关于卷积的定义,可以参考这篇知乎的回答):
\[
f(x,y)*h(x,y)=\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)h(x-m,y-n)
\]
然后,我们对等式两边同时进行傅立叶变换(注意,傅立叶变换是针对x、y进行的,m、n相关的式子可以看作常数):
\[
\begin{eqnarray}
F[f(x,y)*h(x,y)]&=&F[\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)h(x-m,y-n)] \&=&\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)F[h(x-m,y-n)] \\end{eqnarray}
\]
由之前的平移性,我们知道:\(h(x-m,y-n)\Leftrightarrow H(u,v)e^{-j2\pi (um/M+vn/N)}\) 。所以上式中的 \(F[h(x-m,y-n)]=H(u,v)e^{-j2\pi (um/M+vn/N)}\),这样,我们便得到:
\[
\begin{eqnarray}
F[f(x,y)*h(x,y)]&=&\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)F[h(x-m,y-n)] \&=&\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)H(u,v)e^{-j2\pi (um/M+vn/N)} \&=&\sum_{m=0}^{M-1}\sum_{n=0}^{N-1}f(m,n)e^{-j2\pi (um/M+vn/N)} H(u,v) \&=&F(u,v)H(u,v)
\end{eqnarray}
\]
上面的 \(\sum_{m=0}^{M-1} \sum_{n=0}^{N-1} f(m,n)e^{-j2\pi (um/M+vn/N)}\) 刚好凑成一个傅立叶变换 \(F(u,v)\)。所以我们最终证明:\(f(x,y)*h(x,y) \Leftrightarrow F(u,v)H(u,v)\)。
另一个式子 \(F(u,v)*H(u,v) \Leftrightarrow f(x,y)h(x,y)\) 的证明是类似的。
