关于傅立叶变换,知乎上已经有一篇很好的教程,因此,这篇文章不打算细讲傅立叶的物理含义,只是想从图像的角度谈一谈傅立叶变换的本质和作用。
本文假设读者已经熟知欧拉公式:
\[
e^{j\pi x}=\cos{\pi x}+j\sin{\pi x}
\]
并且知道高数课本中给出的傅立叶变换公式:
\[
f(x) ~ \frac{a_0}{2}+\sum_{n=1}^{\infty}{[a_n \cos{nx}+b_n\sin{nx}]}
\]
其中 \(a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\cos{nx}}dx\),\(b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}{f(x)\sin{nx}}dx\)。
当然,线性代数也还是要懂一些的。
图像的表示
傅立叶变换本质上是把信号从时空域变换到频率域。但在图像里面,这个本质又说明什么呢?
为了搞清楚这一点,我们先回顾一下,什么是图像。
通常来说,我们看到的计算机里的图像是一个二维矩阵:

比如,上面这个只有四个像素点的图片,就是一个这样的矩阵(不要在意数值大小,你可以把它们归一化到常用的 0~255 区间,但本质上它们表达的信息是一样的):
\[
\begin{bmatrix}
0.4 & 0.6 \0.8 & 0.2
\end{bmatrix}
\]
假设图像是 \(f(x)\),这个 \(f(x)\) 就是我们常说的信号。这个信号表面上看是一个矩阵,其实它是由几个最基本的向量的线性组合产生的:
\[
f(x)=0.4 \times \begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix}+0.6 \times \begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix}+0.8 \times \begin{bmatrix}0 & 0 \\ 1 & 0 \end{bmatrix}+0.2 \times \begin{bmatrix}0 & 0 \\ 0 & 1 \end{bmatrix}
\]
如果看到这里你有一种恍然大悟的感觉,那你差不多快摸清傅立叶的套路了。
其实,从线性代数的角度出发去思考问题,你会发现,图像这种信息是由一些最基本的元素组合而成的。这些元素在线性代数中被称为基向量,它们构成的集合称为基底。选择不同的基底,信息就可以有多种不同的表示。例如上图中,我们选择的是最常见的基底:
\[
\{\begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix} , \begin{bmatrix}0 & 1 \\ 0 & 0 \end{bmatrix} , \begin{bmatrix}0 & 0 \\ 1 & 0 \end{bmatrix}, \begin{bmatrix}0 & 0 \\ 0 & 1 \end{bmatrix}\}
\]
在这组基底下,图片就表示为:\(\begin{bmatrix} 0.4 & 0.6 \\ 0.8 & 0.2 \end{bmatrix}\)。
如果换成另外一组基底,就会得到另一种表示。甚至,在计算机视觉中,我们常常会提取图像的语义信息,把图像转换到其他一些高维空间。但不管怎样,它们本质上都是从某一个特殊的角度来表示图像这一信息,只是不同的基底下,表示出来的特征有所不同,有些适合肉眼观看,有些适合计算机识别。
那傅立叶变换是想干嘛?其实就是换了另一种基底(正/余弦函数)来表示图像。傅立叶变换之所以重要,是因为它所采用的基底具有一些非常好的性质,可以方便我们对图像进行处理。
傅立叶变换
这一节中,我们就来看看,如何把图像用傅立叶的基底表示出来,也就是我们常说的图像的傅立叶变换。
首先,要明确,在一组基底下,信息的表示是什么。回到上一节的例子,\(f(x)=\begin{bmatrix} 0.4 & 0.6 \\ 0.8 & 0.2 \end{bmatrix}\),有没有发现,在特定基底下,信息是用这些基底线性组合的权重来表示的。只要我们有了这些权重信息,就可以用基底向量的线性组合把信息恢复出来。
因此,对于傅立叶变换而言,我们要求的其实就是基底的权重。
那傅立叶变换的基底是什么呢?如果你看过前面说的那篇教程,你会发现,傅立叶是用无穷多个三角函数的叠加来逼近原来的信号。因此,对于傅立叶变换而言,它的基底其实就是这些三角函数,而我们要求的则是这些函数的线性组合参数。
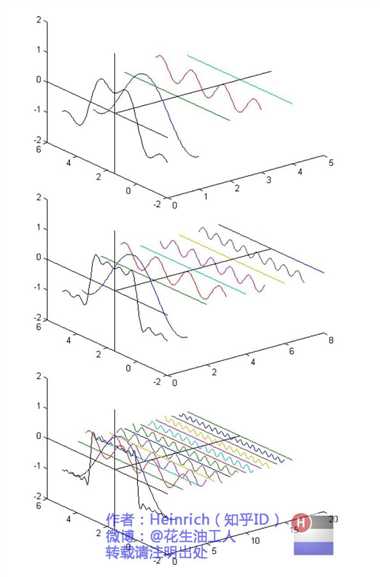
回到最开始的傅立叶公式:
\[
f(x) ~ \frac{a_0}{2}+\sum_{n=1}^{\infty}{[a_n \cos{nx}+b_n\sin{nx}]}
\]
有没有看到,这个公式已经揭示了这些三角函数的系数,也就是我们要求的线性组合参数。公式前面的 \(a_0\) 是可以统一进去的。下面,我们就从它出发,看看如何推导出统一的参数表示。
(??以下是公式重灾区,恐惧者可直接跳到结论部分)
首先,我们考虑更一般的情况,即函数 \(f(x)\) 的周期是 \(T\)(上面这个公式的周期是 \(2\pi\)),然后将 \(f(x)\) 表示成另一种形式:
\[
f(x)=a_0+\sum_{n=1}^\infty {[a_n\cos{\frac{2n\pi x}{T}}+b_n \sin{\frac{2n\pi x}{T}}]}
\]
其中,\(a_0=\frac{1}{T}\int_0^T{f(x)dx}\),\(a_n=\frac{2}{T}\int_{0}^T{f(x)\cos{\frac{2n\pi x}{T}dx}}\),\(b_n=\frac{2}{T}\int_0^T{f(x)\sin{\frac{2n\pi x}{T}dx}}\)。
注意,这个表示和之前的公式没有本质区别。
接下来,对 \(f(x)\) 进行一系列操作:
\[
\begin{eqnarray}
f(x)&=&a_0+\sum_{n=1}^\infty {[a_n\cos{\frac{2n\pi x}{T}}+b_n \sin{\frac{2n\pi x}{T}}]} \&=&a_0+\sum_{n=1}^{\infty}{[a_n\cos{\omega_nx+b_n\sin{\omega_nx}}]} \\
&=&a_0+\sum_{n=1}^\infty{[a_n(\frac{e^{j\omega_n x}+e^{-j\omega_n x}}{2})+b_n(\frac{e^{j\omega_n x}-e^{-j\omega_n x}}{2j})]} \&=&a_0+\sum_{n=1}^\infty{(\frac{a_n-jb_n}{2})e^{j\omega_n x}+\sum_{n=1}^\infty{(\frac{a_n+jb_n}{2})e^{-j\omega_nx}}}
\end{eqnarray}
\]
其中,\(\omega_n=\frac{2n\pi}{T}\)。
下一步,继续化简括号里的东西:
\[
\begin{eqnarray}
\frac{a_n-jb_n}{2}&=&\frac{1}{2}[\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\cos{\omega_n x\ dx-j\frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\sin{\omega_nx\ dx}}] \&=&\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)[\cos{\omega_n x-j\sin{\omega_n x}}]\ dx \&=&\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f(x)e^{-j\omega_n x}}\ dx \&=&c_n
\end{eqnarray}
\]
其中,\(c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f(x)e^{-j\omega_n x}}\ dx\)。
用上面的结果化简公式右边的内容:
\[
\begin{eqnarray}
\sum_{n=1}^\infty{(\frac{a_n+jb_n}{2})e^{-j\omega_n x}}&=&\sum_{n=-\infty}^{-1}{(\frac{a_{-n}+jb_{-n}}{2})e^{-j\omega_{-n}x}} \&=&\sum_{n=-\infty}^{-1}{(\frac{a_n-jb_n}{2})e^{j\omega_n x}} \&=&\sum_{n=-\infty}^{-1}{(\frac{a_n-jb_n}{2})e^{j\omega_n x}} \&=&\sum_{n=-\infty}^{-1}{c_n e^{j\omega_n x}}
\end{eqnarray}
\]
这样一来,我们就得到一个统一的表达式:
\[
\begin{eqnarray}
f(x)&=&a_0+\sum_{n-1}^{\infty}{(\frac{a_n-jb_n}{2})e^{j\omega_n x}+\sum_{n=1}^{\infty}{(\frac{a_n+jb_n}{2})e^{-j\omega_n x}}} \&=&c_0+\sum_{n=1}^{\infty}{c_ne^{j\omega_n x}+\sum_{n=-\infty}^{-1}c_n e^{j\omega_n x}} \&=&\sum_{n=-\infty}^{\infty}{c_ne^{j\omega_n x}}
\end{eqnarray}
\]
码了这么多公式后,我们终于得到了一个关于三角函数的线性组合的形式。再经过傅立叶变换后,函数 \(f(x)\) 就变成了一个向量的形式:\({[\dots, c_{-n}, \dots, c_0, c_1, c_2, \dots, c_n, \dots]}\)。这里的 \(c_n\) 就是我们通常说的傅立叶变换,而公式中的 \(e^{j\omega_nx}\) 就是傅立叶变换的基底。
接下来,我们想知道,对于一张图片而言,这个 \(c_n\) 该怎么求。
我们先考虑一维的情况(你可以想象成一个宽度为 \(N\),高度为 1 的图片)。在公式中,\(c_n=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f(x)e^{-j\omega_n x}}\ dx\),这是对连续函数而言的,但计算机中的图像信号是离散的,因此,我们要把积分符号换成求和符号。另外,周期用图像的宽度代替。这样,我们就得到图像中的傅立叶变换:\(c_n=\frac{1}{N}\sum_{x=0}^{N-1}f(x)e^{-j\omega_n x}\)。
然后,有同学会问,这样的 \(c_n\) 有多少个呢?在我们前面推导的公式中,\(c_n\) 有无穷多个,这时符合傅立叶的前提假设的:无穷多个三角函数的叠加才能构成原来的信号。但是,计算机只能表示有穷的信息,因此,我们需要进行采样。好在,实际情况中,当 \(n\) 的值越来越大时,\(c_n\) 的值会渐渐趋于 0,因为图片中的高频分量往往比较小,所以这一部分高频的三角函数的系数 \(c_n\) 的值也会很小(公式中,频率 \(\omega_n=\frac{2n\pi}{N}\),\(n\) 越大也就表明频率越大)。实际操作中,我们会取 \(N\) 个 \(c_n\),其中 \(N\) 就是图像信号的周期。因此,我们最终得到图像中的傅立叶变换:
\[
F(u)=\frac{1}{N}\sum_{x=0}^{N-1}f(x)e^{-j2\pi ux/N} , \ \ u=0,1,...,N-1
\]
公式中的 \(f(x)\) 指的就是图片中 x 位置的像素值,这也说明,傅立叶变换是综合计算图像像素的整体灰度变化后得到的。如果图像中高频信息比较大(即图像灰度变化很剧烈),则对于频率高的基底向量(\(u\) 的值比较大),其对应的权重 \(F(u)\) 的值也会比较大,反之亦然。
傅立叶逆变换
所谓傅立叶逆变换,就是在得到一堆傅立叶变换的参数 \(F(u)\) 后,如何反推回去,得到空间域的图像。
其实非常简单,前面说了,傅立叶变换就是把时空域下的图像信号 \(f(x)\) 重新用频率域的基底来表示。现在,频率域基底向量的系数 \(F(u,v)\) 已经有了,把它们组合起来就可以得到原来的信号:\(f(x)=\sum_{n=-\infty}^{\infty}{c_ne^{j\omega_n x}}\)。因此,傅立叶逆变换就是把傅立叶基底向量的系数再累加起来:
\[
f(x)=\sum_{u=0}^{N-1}F(u)e^{j2\pi ux/N}, \ \ x=0,1,...,N-1
\]
二维傅立叶
二维傅立叶其实就是在一维的基础上,继续向另一个方向扩展而已,相当于一个二重积分:
\[
\begin{eqnarray}
F(u, v)&=&\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x, y)e^{-j2\pi ux/M}e^{-j2\pi vy/N} \\end{eqnarray}
\]
傅立叶逆变换:
\[
f(x,y)=\sum_{u=0}^{M-1}\sum_{v=0}^{N-1}F(u,v)e^{j2\pi ux/M}e^{j2\pi vy/N}
\]
