cftool
真是神奇,之前我们搞的一些线性拟合解方程,多项式拟合,函数拟合求参数啊,等等。
已经超级多了,为啥还得搞一个cftool拟合啊?而且毫无数学理论。
如果你足够细心,你会发现,之前的拟合,都是我们猜测这个拟合的式子大概是什么形式,只需要求个参数。嘿嘿到底准不准呢? 数据及其简单才会被你发现规律呢!
这里在cftool的帮助下不停的尝试才能得到最好的拟合形式。
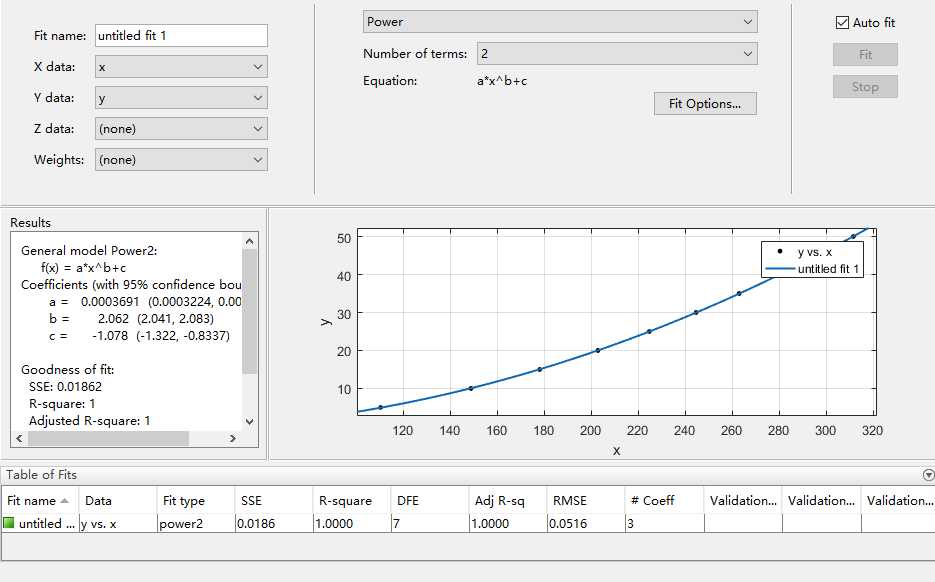

可以看出,拟合形式多样,拟合分析方便。
· Custom Equations:用户自定义的函数类型 · Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x) · Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w) · Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2) · Interpolant:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving · Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~ · Power:幂逼近,有2种类型,a*x^b 、a*x^b + c · Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型 · Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思) · Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1) · Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b)
函数逼近
给一个栗子吧:
? 用 ? 来拟合。
我们已经可以通过自己已经学的办法来解决这个问题了(四个函数都可以使用,大致两条思路)
方法一:首先生成数据,然后写矩阵
方法二:函数形式
(当然还有多项式拟合方法,和解方程法,没想到有不知不觉已经学了5个方法了)
x = -pi/2:pi/100:pi/2; y = cos(x); x = x‘; y = y‘; r = [ones(101,1),x.^2,x.^4]; sx = lsqlin(r,y);
?函数逼近答案:

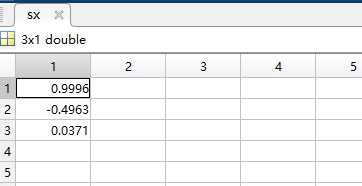
方法二:
x = -pi/2:pi/100:pi/2; y = cos(x); F = @(sx)sx(1)+sx(2)*x.^2+sx(3)*x.^4-y; cs0 = rand(3,1); cs = lsqnonlin(F,cs0);
拟合效果也是杠杠的。
现在还有一个方法,哈哈,开心吧!
老实说,看上去有点像解方程,当然是班门弄斧了,里面的原理已经完全不一样了。
既然已经有函数了,还要麻烦的用这个函数去生成数据吗?
稍微看了一点理论,还是超级复杂的。哈哈,我等人才还得加油了。
看一下格式吧:
clc,clear; syms x; base = [1,x^2,x^4]; y1 = base.‘*base; y2 = cos(x)*base.‘; r1 = int(y1,-pi/2,pi/2); r2 = int(y2,-pi/2,pi/2); a = r1\r2; xishu1 = double(a); xishu2 = vpa(a,6);
至此,第一个数学建模模型,插值和拟合,已经完成了。恭喜啦!!!
