标签:style blog http color 使用 strong 文件 数据 2014
一个真实的例子:根据一家公司服务器过去的访问量来预测未来的访问量。
具体步骤:
1.读取数据:
服务器的访问量被记录成一个csv文件web_traffic.csv,格式如下:
1 2272
2 nan
3 1386
4 1365
5 1488
6 1337
7 1883
8 2283
9 1335
10 1025
11 1139
12 1477
数据中第一列是小时数,第二列是那个小时访问的访问量。使用scipy这个工具将它读入一个scipy自定义的用于科学计算的数组(代码如下):
import scipy as sp data = sp.genfromtxt("web_traffic.tsv",delimiter=‘\t‘)
print data[:10]
上述代码包含打印数据前十行的逻辑,其结果如下。
[[ 1.00000000e+00 2.27200000e+03]
[ 2.00000000e+00 nan]
[ 3.00000000e+00 1.38600000e+03]
[ 4.00000000e+00 1.36500000e+03]
[ 5.00000000e+00 1.48800000e+03]
[ 6.00000000e+00 1.33700000e+03]
[ 7.00000000e+00 1.88300000e+03]
[ 8.00000000e+00 2.28300000e+03]
[ 9.00000000e+00 1.33500000e+03]
[ 1.00000000e+01 1.02500000e+03]]
关于对科学数组的操作,可以参考如下网页:http://wiki.scipy.org/Tentative_NumPy_Tutorial
2.做数据清洗和预处理
我们发现这些数据项中有一些无效的值,瞧见数据中被标红的nan么?这代表了无效信息。我们统计一下样例数据集中无效数据的个数
x = data[:,1]
y = data[:,1]
sp.sum(sp.isnan(y))
我们得到结果为8,也就是8个无效数据,而数据集的个数是743,可以忍。我们把它洗掉。btw,numpy工具还是很方便的。
x = x[~sp.isnan(y)]
y = y[~sp.isnan(y)]
为了得到更加直观的印象,我们将它可视化。这时候就使用到了图形工具Matplotlib. 第一次使用,和Matlib很像,当年可是用Matlib画了不少图。
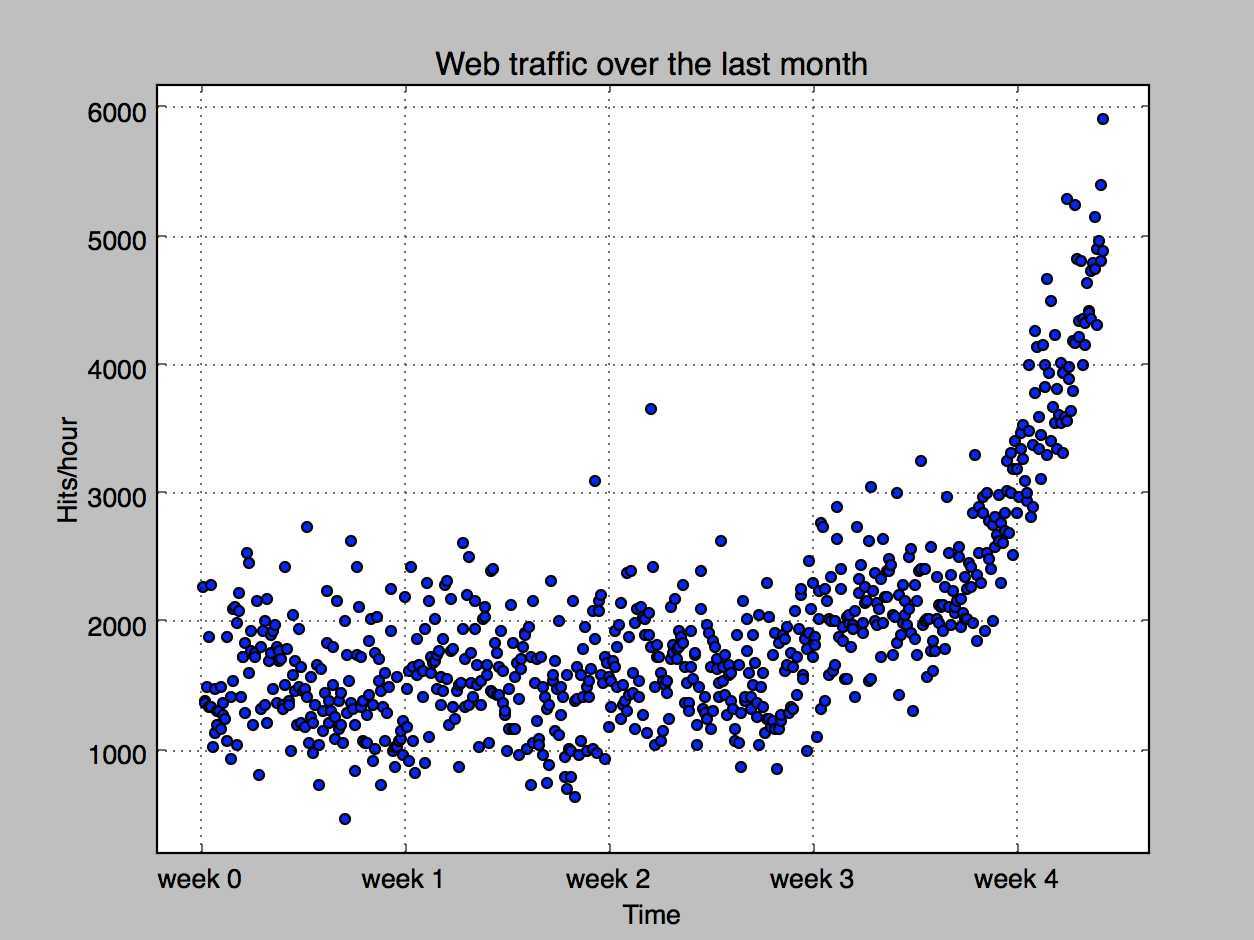
我们看到,很明显趋势是个上升趋势,但怎么做出预测呢?
使用Matplotlib画图的教程如下:http://matplotlib.org/users/pyplot_tutorial.html 不过竟然被墙了,不知道他们墙个科学软件的网站干毛!想看自己想办法,fxxx GFW! pyplot包的用法见下面链接:http://matplotlib.org/api/pyplot_api.html 同样自己想办法。
3.使用正确的模型和学习方法
我们不知道模型是什么,我们要找到它,并且用拟合出来的模型来预测未来!
从上面的图,我第一个印象是我本科时代学的一门课:数值逼近。数值逼近的核心就是根据现有数据找到规律,也就是拟合函数。读下去发现,书中的例子就是一种典型的数值逼近方法,但是记得当时的课程没有迭代和学习这个概念。继续往下看。
假定这个函数为f,那么怎么判定这个函数是一个较好的模型呢?常见的做法就是看样本数据与函数之间的误差和有多大,为了避免负数,一般会用方差。这样就定义了一个函数:
def error(f,x,y): return sp.sum((f(x)-y)**2)
f是什么样子的呢?,最简单的就是一次函数 我们f定义为 f(x) = ax +b 现在的工作就是要确定a和b是什么了。SciPy中有个ployfit函数,可以让我们走捷径。它能够找出a和b,使得上面定义的error返回最小值(也就是对数据最拟合)
fp1, residuals, rank, sv, rcond = sp.polyfit(x,y,1,full =True) print fp1
其中fp1是一个二维数组,里边有a和b的值
打印出来的值为[2.59619213 989.02487106]
我们得到了线性函数 f(x)= 2.59619213x + 989.02487106
它的误差有多大呢?还记得那个error函数么?
我们用如下代码构造一个这样的函数:
f1 = sp.poly1d(fp1) print (error(f1,x,y))
我们得到了一个结果:317389767.34 结果好不好呢?先不说。画张图看看。加入如下代码:
fx = sp.linspace(0,x[-1],1000) #生成X来作图 plt.plot(fx,f1(fx),linewidth=4) #画出曲线 plt.legend(["d=%i" % f1.order],loc ="upper left") #角标
得到的图如下:
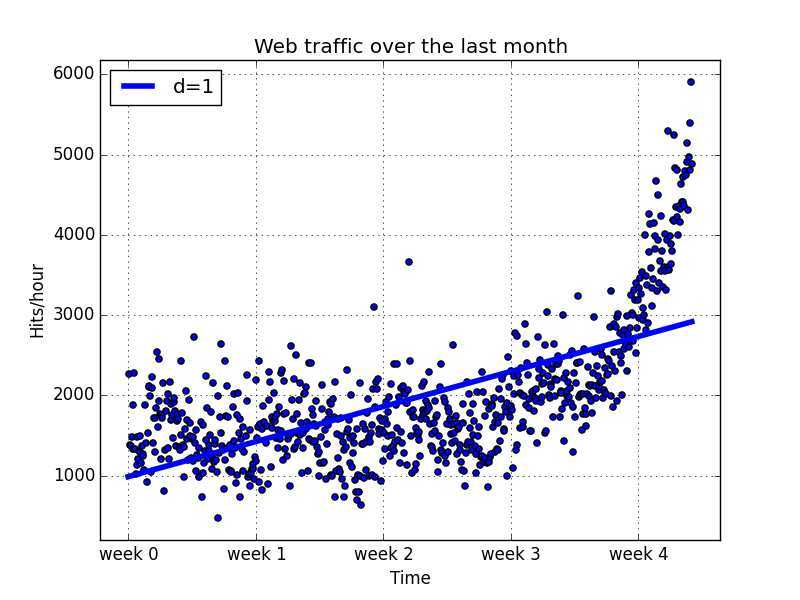
很明显从图里边看出来,从第四周开始,这条直线显然代表不了那些数据点了。317389767.34这个值好不好呢?因为全是做的拟合,肯定都有误差。我们先拿这个数保底,看看能不能找到更好的模型吧。从这里看,显然一次线性函数不是描述模型的好选择。后面就是尝试不同的迭代方法了。 How? 下节继续吧。
btw,要是上大学的时候有这本书该多好!现在的小朋友们真是幸福。想学东西会有这么多好资源。
标签:style blog http color 使用 strong 文件 数据 2014
原文地址:http://www.cnblogs.com/skytraveler/p/3978324.html