https://vjudge.net/problem/UVALive-2218
题意:
铁人三项比赛,每项比赛长度未定,已知每个选手每项比赛的平均速度。
设计每项比赛的长度,让其中某个特定选手获胜。
判断哪些选手有可能 获得冠军,并列不算
每项比赛长度必须>0
线性规划问题
设比赛总长度为1,第一项长度为x,第二项长度为y,第三项长度为1-x-y
则选手i打败选手j的条件是
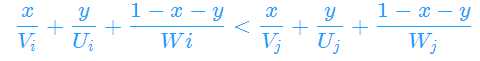
化为Ax+By+C>0,得
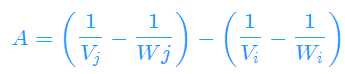
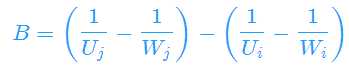
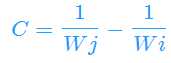
对于每个选手i,都会得到n-1个半平面
再加上x>0,y>0,1-x-y>0
一共n+2个半平面
如果这n+2个半平面有交,那么选手i可能获得冠军
#include<cmath> #include<cstdio> #include<algorithm> #define N 104 using namespace std; const double eps=1e-7; struct Point { double x,y; Point(double x=0,double y=0) : x(x),y(y) { } }; typedef Point Vector; Vector operator + (Vector A,Vector B) { return Vector(A.x+B.x,A.y+B.y); } Vector operator - (Vector A,Vector B) { return Vector(A.x-B.x,A.y-B.y); } Vector operator * (Vector A,double b) { return Vector(A.x*b,A.y*b); } struct Line { Point P; Vector v; double ang; Line() {} Line(Point P,Vector v) :P(P),v(v) { ang=atan2(v.y,v.x); } bool operator < (Line L) const { return ang<L.ang; } }; Line L[N]; double Cross(Vector A,Vector B) { return A.x*B.y-A.y*B.x; } bool OnLeft(Line L,Point p) { return Cross(L.v,p-L.P)>0; } Point GetIntersection(Line a,Line b) { Vector u=a.P-b.P; double t=Cross(b.v,u)/Cross(a.v,b.v); return a.P+a.v*t; } bool HalfplaneIntersection(Line *L,int n) { sort(L,L+n); int first,last; Point *p=new Point[n]; Line *q=new Line[n]; q[first=last=0]=L[0]; for(int i=1;i<n;++i) { while(first<last && !OnLeft(L[i],p[last-1])) last--; while(first<last && !OnLeft(L[i],p[first])) first++; q[++last]=L[i]; if(fabs(Cross(q[last].v,q[last-1].v))<eps) { last--; if(OnLeft(q[last],L[i].P)) q[last]=L[i]; } if(first<last) p[last-1]=GetIntersection(q[last-1],q[last]); } while(first<last && !OnLeft(q[first],p[last-1])) last--; return last-first>1; } int V[N],U[N],W[N]; int main() { int n; while(scanf("%d",&n)!=EOF) { for(int i=0;i<n;++i) scanf("%d%d%d",&V[i],&U[i],&W[i]); for(int i=0;i<n;++i) { int lc=0; bool ok=true; double k=10000; for(int j=0;j<n;++j) if(i!=j) { if(V[i]<=V[j] && U[i]<=U[j] && W[i]<=W[j]) { ok=false; break; } if(V[i]>=V[j] && U[i]>=U[j] && W[i]>=W[j]) continue; double a=(k/V[j]-k/W[j])-(k/V[i]-k/W[i]); double b=(k/U[j]-k/W[j])-(k/U[i]-k/W[i]); double c=k/W[j]-k/W[i]; Point P; Vector v(b,-a); if(fabs(a)>fabs(b)) P=Point(-c/a,0); else P=Point(0,-c/b); L[lc++]=Line(P,v); } if(ok) { L[lc++]=Line(Point(0,0),Vector(0,-1)); L[lc++]=Line(Point(0,0),Vector(1,0)); L[lc++]=Line(Point(0,1),Vector(-1,1)); if(!HalfplaneIntersection(L,lc)) ok=false; } puts(ok ? "Yes" : "No"); } } }
