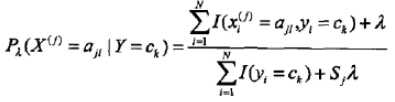朴素贝叶斯法基于
1.贝叶斯定理
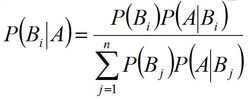
2.特征条件独立假设
用于分类的特征在类(y)确定的情况下是条件独立的
输入:
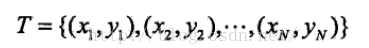
过程:
1.学习先验概率
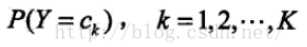
2.学习条件概率分布(条件独立性假设)
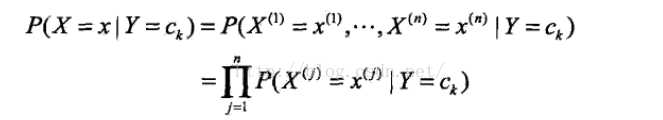
其中:
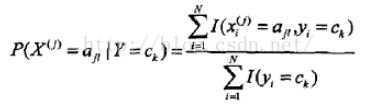 (极大似然估计)
(极大似然估计)
3.根据贝叶斯公式,计算后验概率
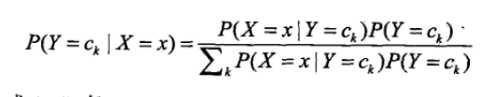
带入条件概率公式:
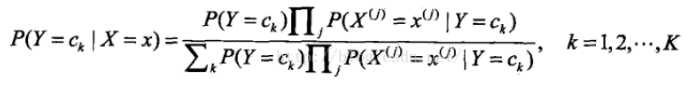
上式中,分母是一样的,当k取不同值时分子是不一样的,得出的后验概率也不一样的,朴素贝叶斯就是要求出最大的后验概率对应的Ck
所以,朴素贝叶斯分类器:
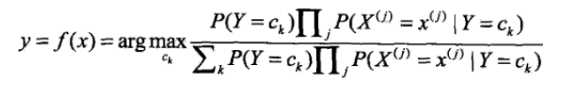
由于分母都是一样的,所以就只计算分子就行:
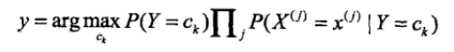
3.输出:分类Ck
将实例分类为后验概率最大的类中,等价于期望风险最小化,证明略
参数估计:(主要是先验概率和条件概率的估计)
极大似然估计:
先验概率:
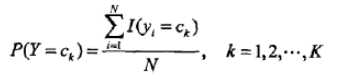
条件概率:
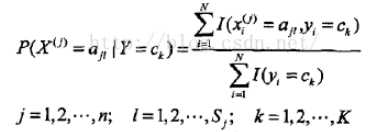
极大似然估计有个缺点是:如果某个特征的条件概率的值为0,那么计算条件概率时会影响其他特征(因为是连乘),所以采用贝叶斯估计,就是在分子、分母都加上一个参数
贝叶斯估计:
先验概率:
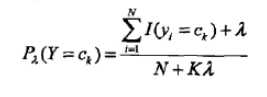
条件概率: