本系列文章只讨论网络流在信息学奥赛中的应用
前言
网络流在信息学奥赛中是一个非常庞大的体系,因为该知识点的模型多变,建模方式复杂,对选手的能力要求较高,因此在各种中高难度级别的比赛中都时常能见到它的身影。(起码SDOI几乎是一年一次)
网络流属于图论问题,而图论问题本质上还是数学问题,因此网络流中的每个结论都能在度娘那里找到详细的证明
概念
有向图:每条边都有方向的图。。
源点 :入度为$0$的点
汇点:出度为$0$的点
(好像不太严谨,大家直观感受一下:joy:)
定义:在有向图$G(V,E)$中,若存在一源点$S$,汇点$T$,且每条边$(u,v)$都有一定的非负容量限制,则称该图为网络流图
煮个栗子
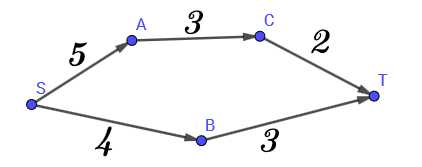
这就是一个标(nan)准(kan)的网络流图
其中S表示源点,T表示汇点,每条边的权值表示流量。
但是光有个图有个毛线用啊,毕竟人家考试不是比谁图画的好看啊:joy:
应用
有了这张图,我们就可以在这上面搞事情啦
最基础的大概有
最大流
无源汇有上下界可行流
有源汇有上下界最大流
有源汇有上下界最小流
最小费用最大流
无源汇上下界最小费用可行流
其中每个部分又有许多经典模型,所以我打算把知识细化开讲,这样方便大家理解
