归并排序求逆序对
题目大意
给你多个序列,让你求出每个序列中逆序对的数量。
输入:每组数据以一个数 n 开头,以下n行,每行一个数字,代表这个序列;
输出:对于输出对应该组数据的逆序对的数量;
顺便在此吐槽一下翻译器,翻译了一顿我啥都看不懂(都怀疑自己是不是中国人了),幸亏自己还能看懂点英语啊。
这个题是机房里一位小伙伴问我我才做的,蒟蒻的我刚开始居然想要双重循环(类似于冒泡排序的方法)来做,看完数据范围之后就放弃了;
然后想到了逆序对是使用归并排序来做的,所以就自己手码了一个归并排序;;可能有的小伙伴还不知道归并排序的思想,所以看了一晚上归并排序的蒟蒻——我,就来给小伙伴们介绍一下吧!
归并排序:
nlog(n)的稳定算法(可用于求逆序对的个数)
应用方法:
二分(所以又叫二路归并)+递归;
为什么使用递归?
answer:要使用归并排序首先就要将数据分解,一直分解到每一个单位,然后就是进行合并了;
如何合并?
answer:比较a[i]和a[j]的大小(其中a[i]属于左区间,a[j]属于右区间,其实就是将左右区间合并、并排序),若a[i]<a[j],则将a[i]复制到r[k]中,然后将r和k都加1,否则将a[j]复制到r[k]中,将r,k加1,最后再将r[k]移动到a[i]中,然后继续合并;
如何求逆序对?
answer:
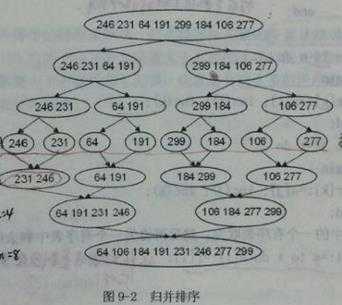
下面就是 归并排序求逆序对 的过程==

1 #include<cstdio> 2 using namespace std; 3 const int maxn=5e5+5; 4 int a[maxn],r[maxn],n;//r[]是辅助用的; 5 long long ans;//ans作为全局变量记录每次逆序对的数量; 6 //记得ans要开long long,否则WAWAWA 7 void msort(int s,int t){ 8 if(s==t) return; 9 int mid=(s+t)>>1;//二进制下右移一位,相当于 /2 ,但是速度更快! 10 msort(s,mid),msort(mid+1,t);//递归的体现 11 int i=s,j=mid+1,k=s; 12 while(i<=mid&&j<=t) 13 if(a[i]<=a[j]) r[k]=a[i],i++,k++; 14 else r[k]=a[j],j++,k++,ans+=mid-i+1; 15 //ans的计算是最神奇的地方,不过动动脑子,画个图啥的也是可以想出来的 16 while(i<=mid) r[k]=a[i],i++,k++; 17 while(j<=t) r[k]=a[j],j++,k++; 18 for(int i=s;i<=t;i++) a[i]=r[i];//每次要更新的是 a[]数组!! 19 } 20 int main(){ 21 while(1){//来一个无限的循环== 22 scanf("%d",&n); 23 if(!n) return 0;//(!n相当于n==0,当然速度也是快一点的啦!)n=0就直接结束程序; 24 for(int i=1;i<=n;i++) scanf("%d",&a[i]); 25 msort(1,n); 26 printf("%lld\n",ans); 27 ans=0;//注意:ans每次都需要清0; 28 } 29 }
--------------------------------------------------下方高能--------------------------------------------
其实只是一个实例,解释一下ans是如何求出来的啦
a[i]↓ ←mid=4→ a[j]↓
3 4 7 9 1 5 8 10
首先将右区间的 1 取出,放到r[k]中,此时 1 是比每个a[i]中的元素都小,也就是说此时i的指针指向 a[1] 的位置,此刻得到的逆序对的数量为 4 ; r[k]= 1 ;
然后再将a[i]和a[j]比较(直到a[i]<a[j]),a[i]<a[j] 将a[i]的元素放到r[k]中; r[k]= 1 3 4;现在a[j]>a[i], i 指向 a[3] 的位置,将5 放到 r[k] 中,得到的逆序对数量为 2 ; r[k]= 1 3 4 5
以此类推,直到进行完归并排序,每次合并都会求出逆序对的数目,即 mid-i+1 ,最后每次将 ans 加上 mid-i+1即可得到最后的答案;
其实求逆序对呢,还可以用线段树,不过对于如此蒟的蒟蒻我,还是算了吧,有兴趣的小伙伴也可以自己从网上搜着看一下,蒟蒻在此就不介绍给大家了(我也不会啊)!

