1.1 定义
定义:假设X服从标准正态分布N(0,1),Y服从 卡方分布,那么 的分布称为自由度为n的t分布,记为 。
分布密度函数 ,其中,Gam(x)为伽马函数。
可用于两组独立计量资料的假设检验。
由于在实际工作中,往往σ(总体方差)是未知的,常用s(样本方差)作为σ总体方差的估计值,为了与u变换(正态化变换)区别,称为t变换,统计量t 值的分布称为t分布。【u分布也叫标准正态分布】
u变换:[(X-μ)/σ]转化成标准正态变量u,以使原来各种形态的正态分布都转换为μ=0,σ=1的标准正态分布(standard normaldistribution),亦称u分布。
在概率论和统计学中,t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。如果总体方差已知(例如在样本数量足够多时),则应该用正态分布来估计总体均值。
经常应用在对呈正态分布的总体的均值进行估计。它是对两个样本均值差异进行显著性测试的学生t测定的基础。t检定改进了Z检定(en:Z-test),不论样本数量大或小皆可应用。在样本数量大(超过120等)时,可以应用Z检定,但Z检定用在小的样本会产生很大的误差,因此样本很小的情况下得改用学生t检定。
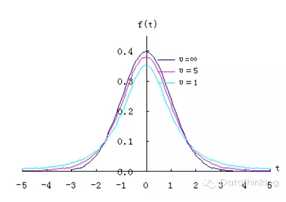
t分布曲线形态与n(确切地说与自由度df)大小有关。与标准正态分布曲线相比,自由度df越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度df愈大,t分布曲线愈接近正态分布曲线,当自由度df=∞时,t分布曲线为标准正态分布曲线。
当总体的标准差是未知的但却又需要估计时,我们可以运用t-分布。
【特征】:
(1)以0为中心,左右对称的单峰分布;
(2)其数学期望E(Z) = 0,n>1;方差D(Z)=n/n-2 , n>2 。
(3)t分布是一簇曲线,其形态变化与n(确切地说与自由度df)大小有关。自由度df越小,t分布曲线越低平;自由度df越大,t分布曲线越接近标准正态分布(u分布)曲线;
(4)随着自由度逐渐增大,t分布逐渐接近标准正态分布。
【本质】:
T分布本质上和标准正态分布没有太大本质差别,可以说就是标准正态分布的一个近似分布。而标准正态分布只是正态分布的一个特殊情况。综上,从本质上说,T分布就是正态分布的一种特殊的近似。
t分布是正态分布的小样本形态。
①正态分布是与自由度无关的一条曲线; t分布是依自由度而变的一组曲线。
② t分布较正态分布顶部略低而尾部稍高。
