一、广度优先遍历
上次我们浅谈了图的深度优先遍历,接下来我们使用广度优先搜索来遍历这个图:
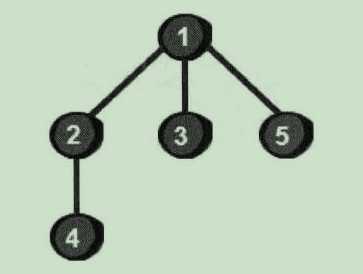
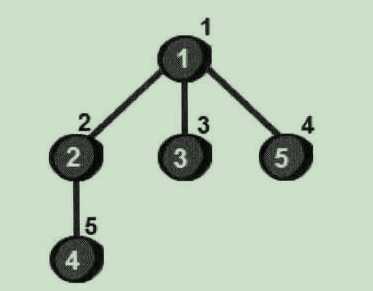
这五个顶点被访问的顺序如下图所示:
二、实现过程
广度优先搜索过程如下:
- 首先以一个未被访问过的顶点作为起始顶点,比如以1号顶点为起点。
- 将1号顶点放入到队列中,然后将与1号顶点相邻的未访问过的顶点,即2号、3号和5号顶点依次放入到队列中。
- 接下来再将2号顶点相邻的未访问过的4号顶点放入到队列中。
- 到此所有顶点都被访问过,遍历结束。
广度优先遍历的主要思想:
- 首先以一个未被访问过的顶点作为起始顶点,访问其所有相邻的顶点;
- 然后对每个相邻的顶点,再访问它们相邻的未被访问过的顶点;
- 直到所有顶点都被访问过,遍历结束。
三、完整代码如下
#include<stdio.h> int main() { int i,j,n,m,a,b,cur,book[101]={0},e[101][101]; int que[10001],head,tail; scanf("%d %d",&n,&m); //初始化二维矩阵 for(i=1;i<=n;i++) for(j=1;j<=n;j++) if(i==j) e[i][j]=0; else e[i][j]=99999999; //表示正无穷 //读入顶点之间的边 for(i=1;i<=m;i++) { scanf("%d %d",&a,&b); e[a][b]=1; e[b][a]=1; } //队列初始化 head=1; tail=1; //从1号顶点出发,将1号顶点加入队列 que[tail]=1; tail++; book[1]=1; //标记1号顶点已访问 //当队列不为空时循环 while(head<tail && tail<=n) { cur=que[head]; //当前正在访问的顶点编号 for(i=1;i<=n;i++) //从1~n依次尝试 { //判断从顶点cur到顶点i是否有边,并且顶点i没有被访问过,则将顶点i入队 if(e[cur][i]==1 && book[i]==0){ que[tail]=i; tail++; book[i]=1; //标记顶点i已访问 } //如果tail大于n,则表明所有顶点都已经被访问过 if(tail>n) { break; } } head++; //当一个顶点扩展结束后,执行head++才能继续往下扩展 } for(i=1;i<tail;i++) printf("%d ",que[i]); getchar();getchar(); return 0; }
