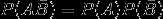， 【随机事件】
A 的对立事件为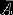 
，A 与 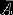有且仅有一个发生。
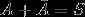
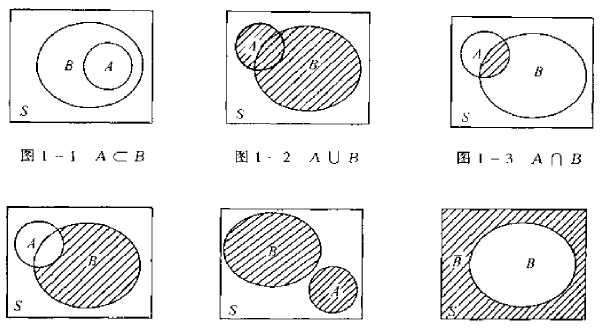
A、B、C 为事件。
交换律：
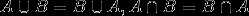
结合律：
, 
分配律：
, 
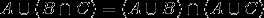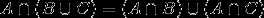
德摩根率：
, 
【随机事件概率】
事件 A 重复 n 次发生的频数为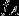 
, 发生的频率为：
（如 ： 事件A为出现正面的硬币，抛硬币重复100 次，若发生频数为40，则发生的频率为 40/100=0.4）
1. 对于任意事件 A ， 有
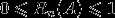
2. 对于必然事件 S，有
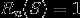
3. 对于互斥事件 A 和 B ，有
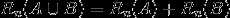
事件A的概率记为 P(A) ,A 的对立事件记为 :
，
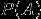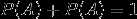
A、B 两个事件,
，
, 
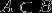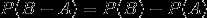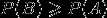
对于任意两个世界 A、B，有:
【古典概率模型】
1. 实验的样本空间只包含有限个样本点；
2. 由于某种对称性，每次实验中，各个基本事件发生的可能性相同。
N(A) 为 A 中包含基本事件的个数 ， N(S) 为基本事件总数。
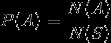
（栗子：两个相同骰子，基本事件总数为6*6=36，都出现相同的点数的事件为6种，该事件概率为1/6）
【条件概率】
B 已发生的条件下A 发生的条件概率，记为 P(A|B) 。
, 
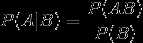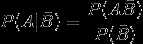
概率的乘法定理，设 P(B)>0 ， 则有
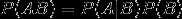
全概率公式：
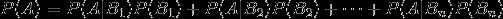
贝叶斯公式：
【事件独立性】
如 P(B|A) = P(B) ，A 发生不改变B发生的概率，则称事件A与事件B相互独立，简称A、B独立（对立事件也独立）。即：
，
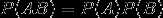