2018冬令营模拟测试赛(十四)
[Problem A]prime
试题描述


输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
题解
考虑 \(\sum_{i=1}^n { 2^{f(i)} }\) 这个式子的组合意义,我们发现 \(2^{f(i)}\) 的意义就是 \(i\) 这个数的每个不同质因子都有选和不选两种方案,\(2^{f(i)}\) 即方案数,也就是说 \(i\) 的无平方因子的约数个数。形式化地,即
\[ 2^{f(i)} = \sum_{d|i} { \mu^2(d) } \]
我们代入到原式当中,得到
\[ \sum_{i=1}^n { 2^{f(i)} } \\\= \sum_{i=1}^n { \sum_{d|i} { \mu^2(d) } } \\\= \sum_{d=1}^n { \mu^2(d) \sum_{d|i, i \le n} { 1 } } \\\= \sum_{d=1}^n { \mu^2(d) \lfloor \frac{n}{d} \rfloor } \]
然而这时 \(\mu^2(d)\) 的前缀和并不好处理,我们考虑给它变个形。先理解一下 \(\mu^2(d)\) 的意义,\(\mu^2(d) = 1 \Leftrightarrow d 没有平方因子 \Leftrightarrow d 的最大完全平方约数 = 1\),假设 \(g(d)\) 就是 \(d\) 的最大完全平方约数,于是上面的条件又等价于 \(\sqrt{g(d)} = 1\),于是可以把式子变成如下形态
\[ \mu^2(d) \\\= [\sqrt{g(d)} = 1] \\\= \sum_{i|\sqrt{g(d)}} { \mu(i) } \\\= \sum_{i^2|g(d)} { \mu(i) } \\\= \sum_{i^2|d} { \mu(i) } \]
然后代入到上式中,得到
\[ \sum_{d=1}^n { \mu^2(d) \lfloor \frac{n}{d} \rfloor } \\\= \sum_{d=1}^n { \lfloor \frac{n}{d} \rfloor \sum_{i^2|d} { \mu(i) } } \\\= \sum_{i=1}^{\lfloor \sqrt{n} \rfloor} { \mu(i) \sum_{i^2|d, d \le n} { \lfloor \frac{n}{d} \rfloor } } \\\= \sum_{i=1}^{\lfloor \sqrt{n} \rfloor} { \mu(i) \sum_{d=1}^{\lfloor \frac{n}{i^2} \rfloor} { \lfloor \frac{\lfloor \frac{n}{i^2} \rfloor}{d} \rfloor } } \]
于是可以预处理 \(\mu(i)\) 的前缀和,然后分段算后面那坨 sigma,sigma 里面的也暴力分段算,最后时间复杂度是 \(O(\sqrt{n}\log n)\) 的(这个可以积分一下算出来)。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <cmath>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
#define LL long long
LL read() {
LL x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 1000010
#define MOD 998244353
#define LL long long
bool vis[maxn];
int prime[maxn], cp, mu[maxn], su[maxn];
void init(int n) {
mu[1] = su[1] = 1;
rep(i, 2, n) {
if(!vis[i]) prime[++cp] = i, mu[i] = -1;
for(int j = 1; j <= cp && i * prime[j] <= n; j++) {
vis[i*prime[j]] = 1;
if(i % prime[j] == 0) {
mu[i*prime[j]] = 0;
break;
}
mu[i*prime[j]] = -mu[i];
}
su[i] = su[i-1] + mu[i];
}
return ;
}
int calc(LL n) {
int ans = 0;
for(LL i = 1; i <= n; ) {
LL r = min(n / (n / i), n);
ans += (LL)(r - i + 1) * (n / i) % MOD;
if(ans >= MOD) ans -= MOD;
i = r + 1;
}
return ans;
}
int main() {
LL n = read();
int m = sqrt(n + .5);
init(m);
int ans = 0;
for(int i = 1; i <= m; ) {
int r = min((int)sqrt(n / (n / ((LL)i * i)) + .5), m);
ans += ((LL)(su[r] - su[i-1]) * calc(n / ((LL)i * i)) % MOD + MOD) % MOD;
if(ans >= MOD) ans -= MOD;
i = r + 1;
}
printf("%d\n", ans);
return 0;
}[Problem B]final
试题描述

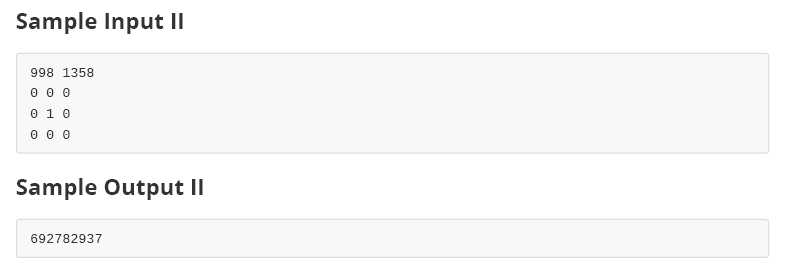
输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
补充:\(1 \le m \le 3n\)。
题解
这题和某道我之前做过的题(那场比赛的 C 题)做法一样,我们发现每个转移都是平移然后叠加上去,所以可以看成多项式乘上 \(x^t\),然后将所有状态、转移都转化成点值就可以直接做矩阵快速幂了。注意这题不需要循环卷积,直接开成 \(3n\) 大小 FFT 就好了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
int read() {
int x = 0, f = 1; char c = getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = getchar(); }
return x * f;
}
#define maxn 2510
#define maxm 8200
#define MOD 998244353
#define Groot 3
#define LL long long
int A[3], all, cbit[8], trans[8][8];
bool Can(int s) {
rep(i, 0, 1) if((s >> i & 1) && (s >> i + 1 & 1) && ((A[1] & 1) || (A[1] >> 2 & 1))) return 0;
return 1;
}
int Pow(int a, int b) {
int ans = 1, t = a;
while(b) {
if(b & 1) ans = (LL)ans * t % MOD;
t = (LL)t * t % MOD; b >>= 1;
}
return ans;
}
int N, brev[maxm];
void FFT(int *a, int len, int tp) {
int n = 1 << len;
rep(i, 0, n - 1) if(i < brev[i]) swap(a[i], a[brev[i]]);
rep(i, 1, len) {
int wn = Pow(Groot, MOD - 1 >> i);
if(tp < 0) wn = Pow(wn, MOD - 2);
for(int j = 0; j < n; j += 1 << i) {
int w = 1;
rep(k, 0, (1 << i >> 1) - 1) {
int la = a[j+k], ra = (LL)w * a[j+k+(1<<i>>1)] % MOD;
a[j+k] = (la + ra) % MOD;
a[j+k+(1<<i>>1)] = (la - ra + MOD) % MOD;
w = (LL)w * wn % MOD;
}
}
}
if(tp < 0) rep(i, 0, n - 1) a[i] = (LL)a[i] * Pow(n, MOD - 2) % MOD;
return ;
}
void prod(int *a, const int *b, const int *c) {
rep(i, 0, N - 1) {
a[i] += (LL)b[i] * c[i] % MOD;
if(a[i] >= MOD) a[i] -= MOD;
}
return ;
}
struct Matrix {
int A[8][8][maxm], n, m;
Matrix() {}
Matrix(int _, int __): n(_), m(__) {}
Matrix operator = (const Matrix& t) {
n = t.n; m = t.m;
rep(i, 0, n) rep(j, 0, m) rep(k, 0, N - 1) A[i][j][k] = t.A[i][j][k];
return *this;
}
Matrix operator * (const Matrix& t) const {
Matrix ans(n, t.m);
rep(i, 0, ans.n) rep(j, 0, ans.m) {
int *a = ans.A[i][j];
rep(k, 0, N - 1) a[k] = 0;
rep(k, 0, m) prod(a, A[i][k], t.A[k][j]);
}
return ans;
}
Matrix operator *= (const Matrix& t) {
*this = *this * t;
return *this;
}
} base(7, 0), tr(7, 7);
Matrix PowM(Matrix& a, int b) {
Matrix ans = a, t = a; b--;
while(b) {
if(b & 1) ans *= t;
t *= t; b >>= 1;
}
return ans;
}
int main() {
int n = read(), m = read();
rep(i, 0, 2) rep(j, 0, 2) A[i] |= (read() << j);
all = 7;
memset(trans, -1, sizeof(trans));
rep(i, 1, all) cbit[i] = cbit[i-(i&-i)] + 1;
rep(s, 0, all) if(Can(s)) {
int ban = 0;
rep(i, 0, 2) if(s >> i & 1) ban |= i < 2 ? (A[2] >> 1 - i) : (A[2] << 1);
rep(ts, 0, all) if(Can(ts) && !(ban & ts)) {
int tb = 0;
rep(i, 0, 2) if(ts >> i & 1) tb |= i < 2 ? (A[0] >> 1 - i) : (A[0] << 1);
if(tb & s) continue;
trans[ts][s] = cbit[ts];
// printf("%d -> %d %d\n", s, ts, trans[ts][s]);
}
}
N = 1; int len = 0;
while(N <= 3 * n) N <<= 1, len++;
rep(i, 0, N - 1) brev[i] = (brev[i>>1] >> 1) | ((i & 1) << len >> 1);
memset(base.A, 0, sizeof(base.A));
base.A[0][0][0] = 1;
FFT(base.A[0][0], len, 1);
memset(tr.A, 0, sizeof(tr.A));
rep(ts, 0, all) rep(s, 0, all) {
if(trans[ts][s] >= 0) tr.A[ts][s][trans[ts][s]] = 1;
FFT(tr.A[ts][s], len, 1);
// printf("tr[%d][%d]: ", ts, s); rep(i, 0, N - 1) printf("%d%c", tr.A[ts][s][i], i < N - 1 ? ‘ ‘ : ‘\n‘);
}
base = PowM(tr, n) * base;
int ans = 0;
rep(s, 0, all) {
FFT(base.A[s][0], len, -1);
// printf("%d: ", s); rep(i, 0, N - 1) printf("%d%c", base.A[s][0][i], i < N - 1 ? ‘ ‘ : ‘\n‘);
ans += base.A[s][0][m];
if(ans >= MOD) ans -= MOD;
}
printf("%d\n", ans);
return 0;
}[Problem C]gift
试题描述


输入
见“试题描述”
输出
见“试题描述”
输入示例
见“试题描述”
输出示例
见“试题描述”
数据规模及约定
见“试题描述”
这题出锅啦,答案下取整改成上取整减 \(1\)。
题解
看到分数就分数规划(二分),现在就是判断是否存在方案使得 \(\frac{B}{A} > x\),移项得到 \(B - Ax > 0\),于是最大化 \(B - Ax\),我们先将所有的好感度都选上,然后就有两种代价,一个是牺牲某个好感度,一个是买某个物品,于是这就是经典的最小割模型了。
用最大权闭合子图的模型会有 \(n + m + 2\) 个点,就 T 飞了,要优化。每条边可以用方程算一下定多少流量,这样就只有 \(n + 2\) 个点了,然后把重边缩掉卡卡常数就 A 了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
#include <map>
using namespace std;
#define rep(i, s, t) for(int i = (s), mi = (t); i <= mi; i++)
#define dwn(i, s, t) for(int i = (s), mi = (t); i >= mi; i--)
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 204010
#define maxm 416010
#define oo 2147483647
struct Edge {
int from, to, flow;
Edge() {}
Edge(int _1, int _2, int _3): from(_1), to(_2), flow(_3) {}
};
struct Dinic {
int s, t, n, m, head[maxn], nxt[maxm];
Edge es[maxm];
int vis[maxn], Q[maxn], hd, tl;
int cur[maxn];
void init() {
m = 0; memset(head, -1, sizeof(head));
return ;
}
void setn(int _) {
n = _;
return ;
}
void AddEdge(int a, int b, int c, int revc = 0) {
es[m] = Edge(a, b, c); nxt[m] = head[a]; head[a] = m++;
es[m] = Edge(b, a, revc); nxt[m] = head[b]; head[b] = m++;
return ;
}
bool BFS() {
memset(vis, 0, sizeof(vis));
vis[t] = 1;
hd = tl = 0; Q[++tl] = t;
while(hd < tl) {
int u = Q[++hd];
for(int i = head[u]; i != -1; i = nxt[i]) {
Edge& e = es[i^1];
if(!vis[e.from] && e.flow) vis[e.from] = vis[u] + 1, Q[++tl] = e.from;
}
}
return vis[s] > 1;
}
int DFS(int u, int a) {
if(u == t || !a) return a;
int flow = 0, f;
for(int& i = cur[u]; i != -1; i = nxt[i]) {
Edge& e = es[i];
if(vis[e.to] == vis[u] - 1 && (f = DFS(e.to, min(a, e.flow)))) {
flow += f; a -= f;
e.flow -= f; es[i^1].flow += f;
if(!a) return flow;
}
}
return flow;
}
int MaxFlow(int _s, int _t) {
s = _s; t = _t;
int flow = 0;
while(BFS()) {
rep(i, 1, n) cur[i] = head[i];
flow += DFS(s, oo);
}
return flow;
}
} sol;
#define maxgift 4010
#define maxcond 200010
#define pii pair <int, int>
#define x first
#define y second
#define mp(x, y) make_pair(x, y)
int CntP;
struct Point {
int id;
Point(): id(0) {}
int p() { return id ? id : id = ++ CntP; }
} gift[maxgift], S, T;
int n, m, sum, mn, price[maxgift], gid[maxgift], half[maxcond], val[maxcond], deg[maxgift];
map <pii, int> cond;
bool check(int x) {
for(int i = 0; i < sol.m; i += 2) sol.es[i].flow += sol.es[i^1].flow, sol.es[i^1].flow = 0;
rep(i, 1, n) sol.es[gid[i]].flow = price[i] * x;
rep(i, 1, m) if(half[i] >= 0) sol.es[half[i]].flow = sol.es[half[i]^1].flow = val[i];
int flow = sol.MaxFlow(S.p(), T.p());
return sum - flow > 0;
}
int main() {
n = read(); m = read(); sum = 0; mn = oo;
sol.init();
rep(i, 1, n) gid[i] = sol.m, sol.AddEdge(S.p(), gift[i].p(), price[i] = read() << 1), mn = min(mn, price[i]);
memset(half, -1, sizeof(half));
rep(i, 1, m) {
int a = read(), b = read(); int now = read();
if(a > b) swap(a, b);
if(!cond.count(mp(a, b))) cond[mp(a,b)] = i;
val[cond[mp(a,b)]] += now;
deg[a] += now; deg[b] += now;
sum += now << 1;
}
for(map <pii, int> :: iterator i = cond.begin(); i != cond.end(); i++)
half[i->y] = sol.m, sol.AddEdge(gift[i->x.x].p(), gift[i->x.y].p(), val[i->y], val[i->y]);
rep(i, 1, n) sol.AddEdge(gift[i].p(), T.p(), deg[i]);
sol.setn(CntP);
int l = 0, r = sum / mn + 1;
while(r - l > 1) {
int mid = l + r >> 1;
if(check(mid)) l = mid; else r = mid;
}
printf("%d\n", l);
return 0;
}