矩阵:一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起,所以有时候可以简便地表示一些复杂的模型。在数学中,一个矩阵说穿了就是一个二维数组。
单位矩阵:从左上角到右下角的对角线(称为主对角线)上的元素均为1。除此以外全都为0。
对称矩阵:如果方阵满足,即,则称A为对称矩阵.它的元素以主对角线为对称轴对应相等.
矩阵加减法:两个矩阵相加减,即它们相同位置的元素相加减,满足交换律和结合律。只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减法运算才有意义,即加减运算是可行的.
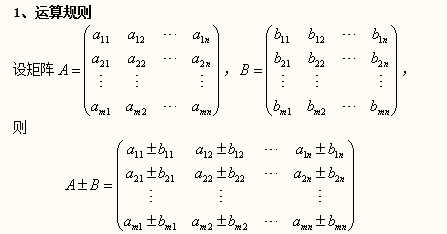
矩阵乘法:矩阵乘法是一种高效的算法可以把一些一维递推优化到log( n ),还可以求路径方案等,所以更是一种应用性极强的算法。
1.矩阵与数的乘法:数乘矩阵A,就是将数乘矩阵A中的每一个元素,记为或.特别地,称称为的负矩阵.满足结合律和分配律。
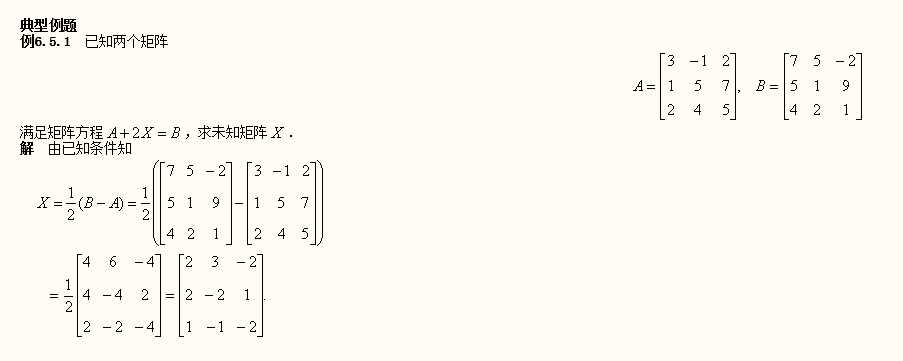
2.矩阵与矩阵的乘法:只有当矩阵A的列数与矩阵B的行数相等时A×B才有意义。一个m×n的矩阵a(m,n)左乘一个n×p的矩阵b(n,p),会得到一个m×p的矩阵c(m,p),矩阵乘法满足结合率,但不满足交换率。一个n行m列的矩阵可以乘以一个m行p列的矩阵,得到的结果是一个n行p列的矩阵。方阵A和它同阶的单位阵作乘积,结果仍为A,即.单位阵在矩阵乘法中的作用相当于数1在我们普通乘法中的作用。运算规则:
设,,则A与B的乘积是这样一个矩阵:
(1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即.
(2) C的第行第列的元素由A的第行元素与B的第列元素对应相乘,再取乘积之和.
(3)两个非零矩阵的乘积可以是零矩阵.由此若,不能得出或的结论.



矩阵转置:将矩阵A的行换成同序号的列所得到的新矩阵称为矩阵A的转置矩阵,记作或.第i行变第J列。Aij变成Aji。
运算性质(假设运算都是可行的)
(1)
(2)
(3)
(4) ,是常数.
矩阵行列式:基于矩阵所包含的行列数据计算得到的一个标量;
二维矩阵[{a,c},{b,d}]的行列式等于:det(A) = ab-cd。
n维矩阵的行列式:假设矩阵A为n维的方阵,定义Aij为从A中删除第i行、第j列之后剩下的n-1维方阵。
可以沿着A的第一行来求取行列式:det(A) = a11*A11-a12*A12+...+a1n*A1n,这是一个递归的定义,包含n项,每一项的正负号等于 (-1)的(i+j)次方。
实际上可以对A的任意一行、任意一列按上面的方法来求取行列式,可以挑选包含0比较多得行(列)。
两个二维向量v1,v2,可以作为平行四边形的临边来定义一个平行四边形。两个向量构成矩阵A={v1,v2},那么平行四边形的面积 = det(A)的绝对值。
矩阵行列式的一些规律
1)如果矩阵A= {r1,r2,...ri...,rn} B={r1,r2,...ri‘,...rn} C={r1,r2,...ri+ri‘,...rn},则有det(C) = det(A)+det(B)
2)如果矩阵A有两行(列)相等则,det(A) = 0
3)如果矩阵A将两行交换后得到矩阵B,则有det(A)=-det(B)
4)如果矩阵A进行行变换后得到矩阵B,则有det(A)=det(B);可以通过行变换达到3)的效果,这个过程中会发生-1数乘某行。
