评分卡系列（三）：分类学习器的评估

时间：2018-01-14 21:21:17 阅读：2076 评论：0 收藏：0 [点我收藏+]

作者：JSong 时间：2018.01.14

评分卡可以用来预测客户的好坏。当一个评分卡已经构建完成，并且有一组个人分数和其对应的好坏状态的数据时，我们想知道所构建的评分卡是否可靠？可靠程度如何？而这取决于如何去定义这个“好”字。一般有三种角度可以来评估：

评分卡分类划分的准确程度，如错误率、准确率、召回率、F1
评分卡的判别能力，评估评分卡将好人和坏人分离开的程度，如KS统计量、ROC曲线、GINI系数
评分卡概率预测的校准精度

为了后面讨论简单，我们假设模型输出的是从0到1000的信用评分(用预测概率线性变换即可)。当选定好一个阈值 c 后，我们把分数 s 大于 c的判定为好人，小于 c 的判定为坏人。以我们在本系列第二篇文章中的结果为例，下图是好人/坏人的密度函数和对应的ROC曲线。

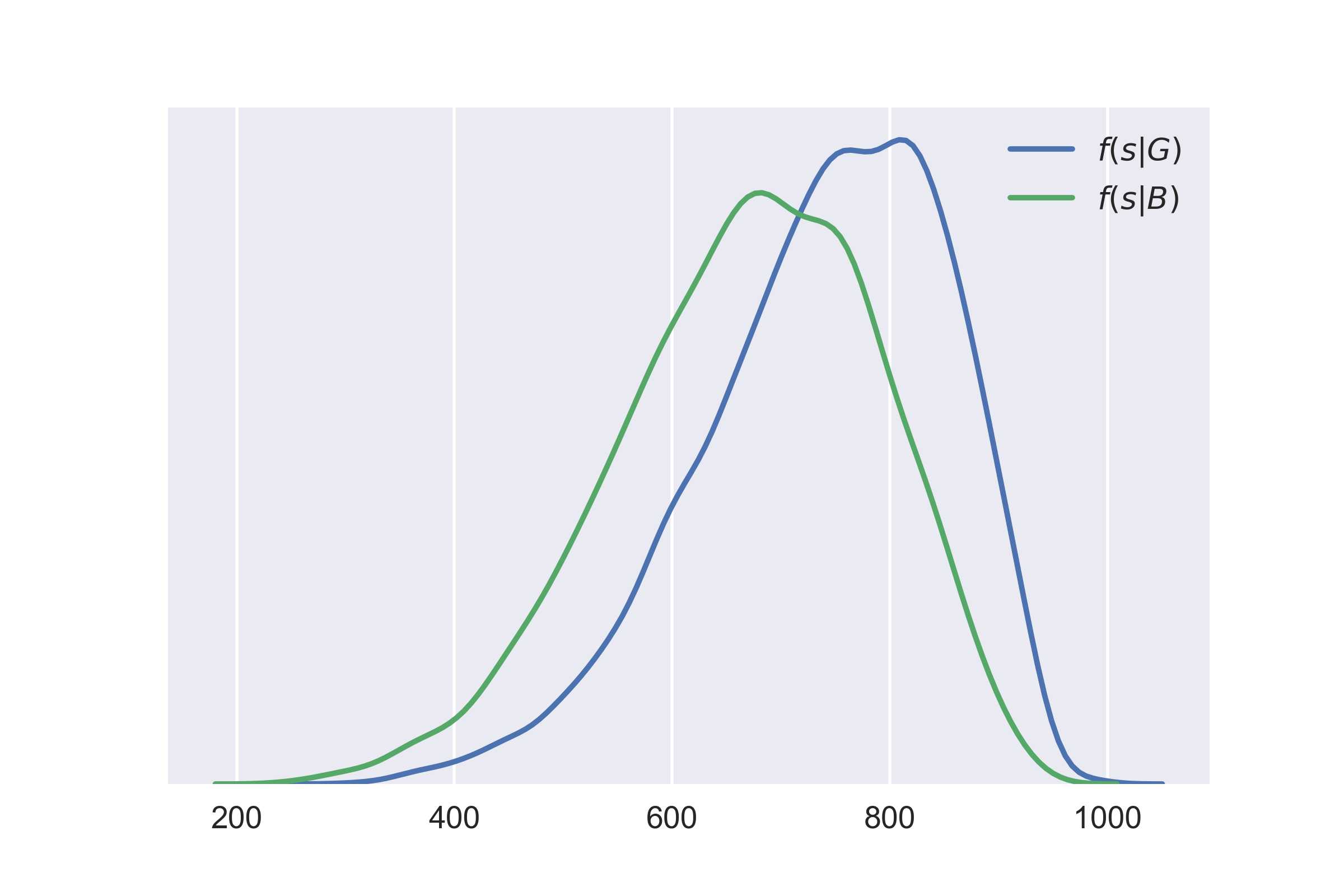
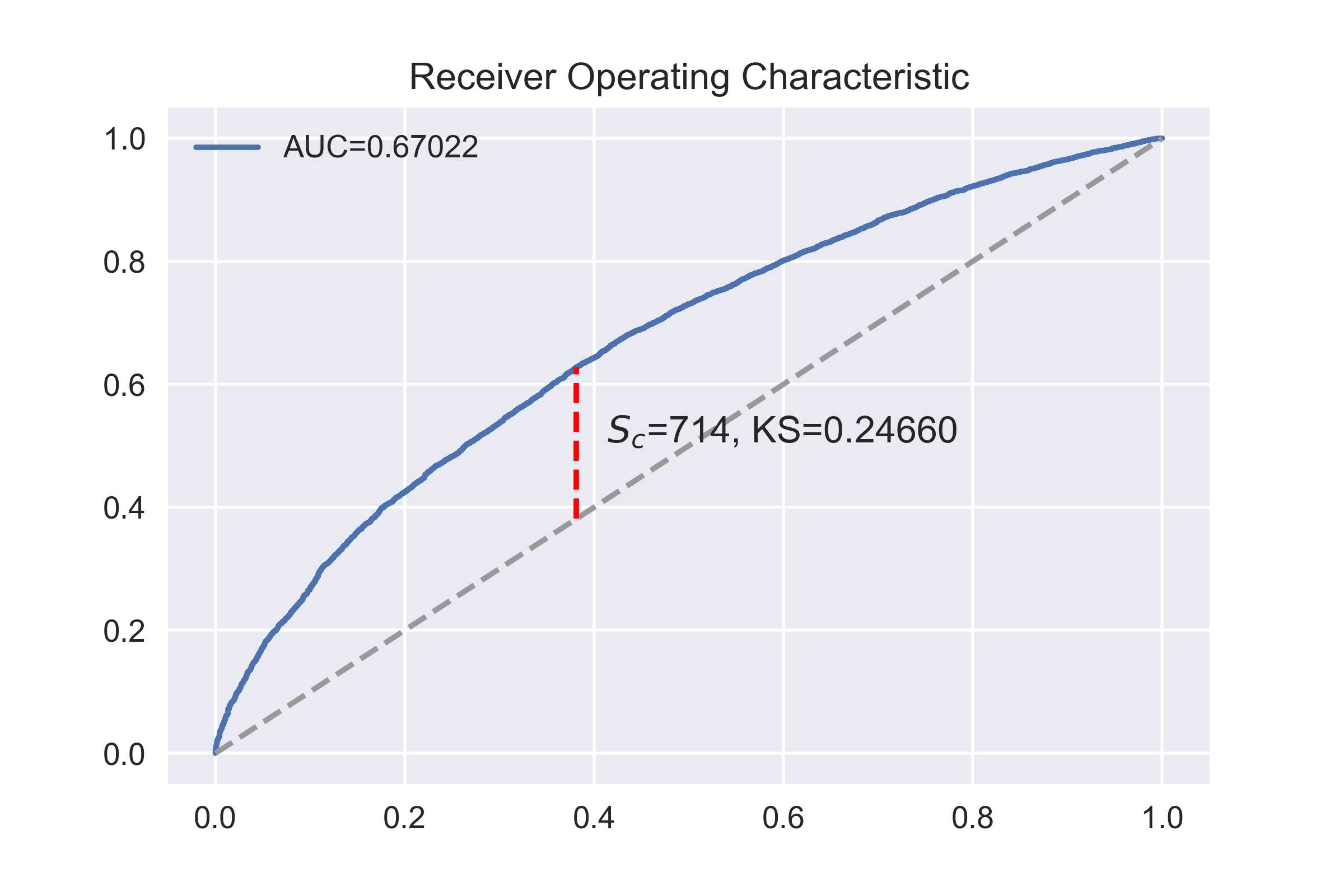
技术分享图片

阈值的选取标准可以按照ROC曲线中的KS统计量来选取，也可以按照最大的 F1 分数来。这里我们选用第一种方法，可以得到了下面的混淆矩阵：

	预测坏人	预测好人
实际坏人	440(2.6%)	4373(25.5%)
实际好人	379(2.2%)	11990(69.8%)

接下来我将从四个方面来评估分类学习器的性能

一般的分类学习器的性能度量
基于随机变量密度函数的评估
基于随机变量分布函数的评估
基于实验的估计方法

我们先从一般的分类学习器的性能度量开始，此时因为因变量的类别数可能大于2，所以更多的是分类的准确度上来考量的。

1、一般的分类学习器的性能度量

在预测任务中，给定样例集

\[D=[(x_1,y_1),(x_2,y_2),\dots,(x_m,y_m)]\]

其中 y_i 是示例 x_i 的真实标记。要评估学习器 f 的性能，就要把学习器预测结果 f(x) 与真实标记进行比较。

在回归任务中，最常用的性能度量是“均方误差”（mean squared eror，MSE）

\[E(f;D)=\int_{D}(f(x)-y)^2p(x)dx=\frac{1}{m}\sum_{i=1}^{m}(f(x_i)-y_i)^2\]

在分类任务中，最常用的有错误率和精度。给定样例集D，分类错误率可以定义为：

\[E(f;D)=\int_{D}\mathbb{I}(f(x)\neq\,y)p(x)dx=\frac{1}{m}\sum_{i=1}^{m}\mathbb{I}(f(x_i)\ \neq\ y_i)\]

精度则定义为

\[acc(f;D)=\int_{D}\mathbb{I}(f(x)=y)p(x)dx=\frac{1}{m}\sum_{i=1}^{m}\mathbb{I}(f(x_i)\ =\ y_i)\]

在评分模型中，精度的计算方法就是

\[acc=\frac{预测类别==实际类别的样本数}{总样本数}\]

1.1 准确率、召回率与F1

假定农夫拉来一车西瓜，我们用训练好的模型对这些西瓜进行判别，显然，错误率衡量了有多少比例的瓜被判别错误。但是若我们关心的是“挑出的西瓜中有多少比例是好瓜”，或者“所有好瓜中有多少比例被挑了出来”，那么错误率显然就不够用了。

对于二分类问题，可将样本根据其真实类别与学习器预测类别的组合划分为真正例（true positive）、假正例（false positive）、真反例（true negative）、假反例（false negative）四种情形。分类结果的 混淆矩阵 如下表所示：

	预测正例	预测反例
实际正例	TP（真正例）	FN（假反例）
实际反例	FP（假正例）	TN（真反例）

我们将 准确率(P,查准率) 与 召回率(R,查全率) 分别定义如下

\[P=\frac{TP}{TP+FP}\]
\[R=\frac{TP}{TP+FN}\]

准确率和召回率是一对矛盾的度量。在垃圾邮件分类模型中，我们更加看重准确率，因为预测为垃圾邮件的实例中要尽可能少的出现正常邮件。而在生产线的次品判定模型中，我们更看重召回率，因为预测是正品的实例中要尽可能少的出现次品（这样需要召回的商品就少）。

将准确率作为y轴，召回率作为x轴，可以得到P-R曲线，其直观显示出分类学习期在样本集上的准确率、召回率。另外为综合考虑两个指标，我们有P和R的调和平均数，F1度量：

\[F1=\frac{2\times\text{P}\times\text{R}}{\text{P}+\text{R}}\]

有时候要调整准确率或者召回率的权重，这时候可以用加权后的F1度量：

\[F1=\frac{(1+\beta)\times\text{P}\times\text{R}}{\beta\times\text{P}+\text{R}}\]

其中β>0度量了召回率相对准确率的重要性，β>1时召回率有更大影响。

注：相对于几何平均数和算术平均数，调和平均数更注重较小者，且当各平均数相等时，调和平均数对应的P和R之间的差值相对更小。

在本文的评分模型中，准确率=440/(440+379)=53.7%, 召回率=440/(440+4373)=9.1%, F1=15.6%. P-ROC曲线是:

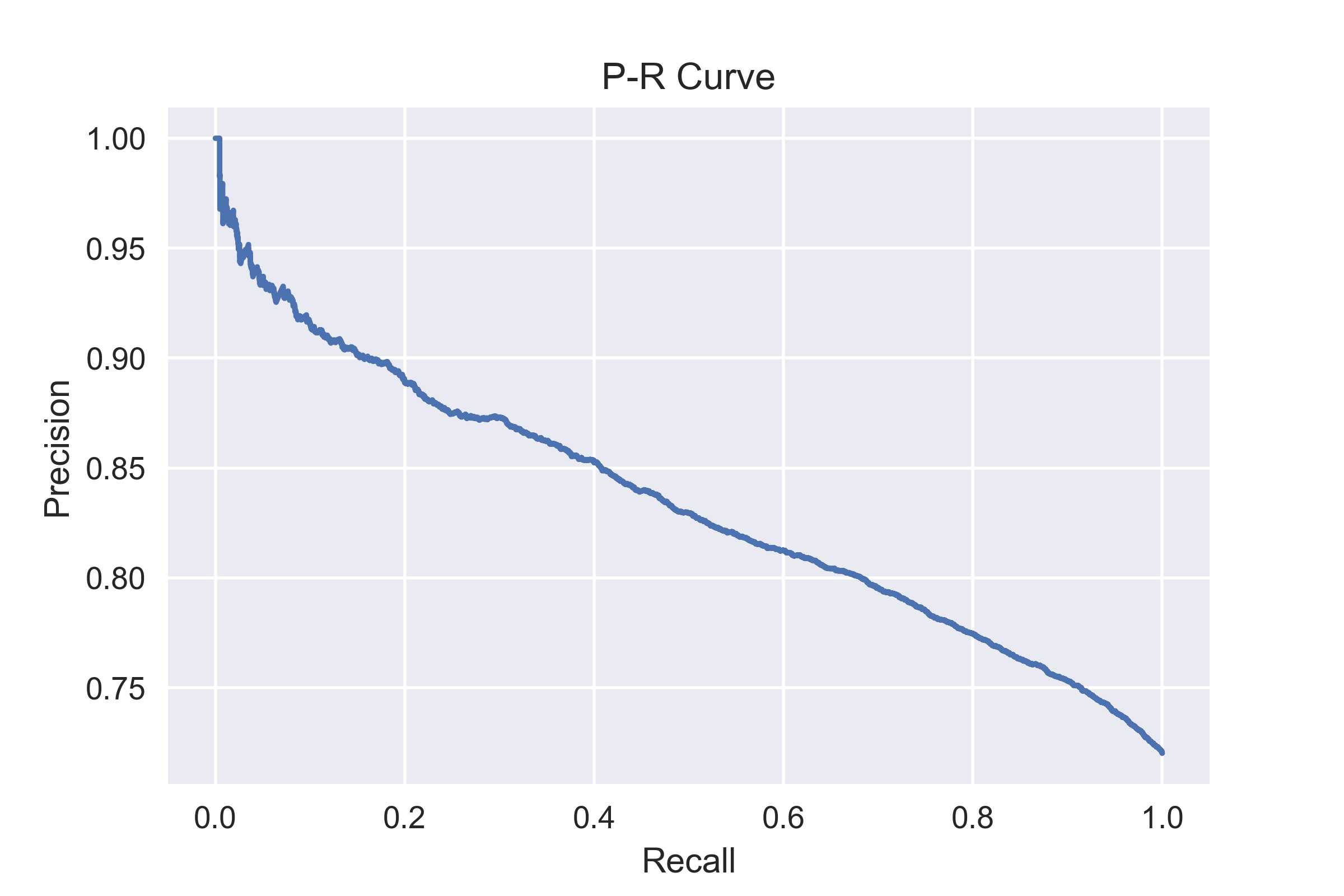
技术分享图片

请忽略效果，我会在本系列的最后一篇文章中来提高模型效果。

1.2 代价敏感错误率与代价曲线

以二分类任务为例，我们可以设定一个“代价矩阵”。

	预测正例	预测反例
实际正例	0	cost1
实际反例	cost2	0

令 \(D^+\) 与 \(D^-\) 分别代表样例集D的正例子集和反例子集，则可以定义“代价敏感错误率为 ”：

\[E(f;\text{cost})=\frac{1}{m}(\sum_{x_i\in\ D^{+}}\mathbb{I}(f(x_i)\ne\ y_i)\times\text{cost1}+\sum_{x_i\in\ D^{-}}\mathbb{I}(f(x_i)\neq\ y_i)\times\text{cost2})\]

代价敏感错误率实现的效果与样本不平衡中的上下采样类似（可参考本公众号的文章《讲讲样本不平衡问题》）,cost1 相对于cost2 越大，等价于正例被抽中的概率越大。所以该方法常用于样本不平衡问题，在一些特定领域，可能比采样的效果要好。

2、基于随机变量密度函数的评估

如下图，是两组好人和坏人的条件概率密度函数图，很明显上图更好，因为好人和坏人的信用评分分离的很好。这一节我们从两个概率密度函数的差异性入手，分析分类学习期的性能评估方法。

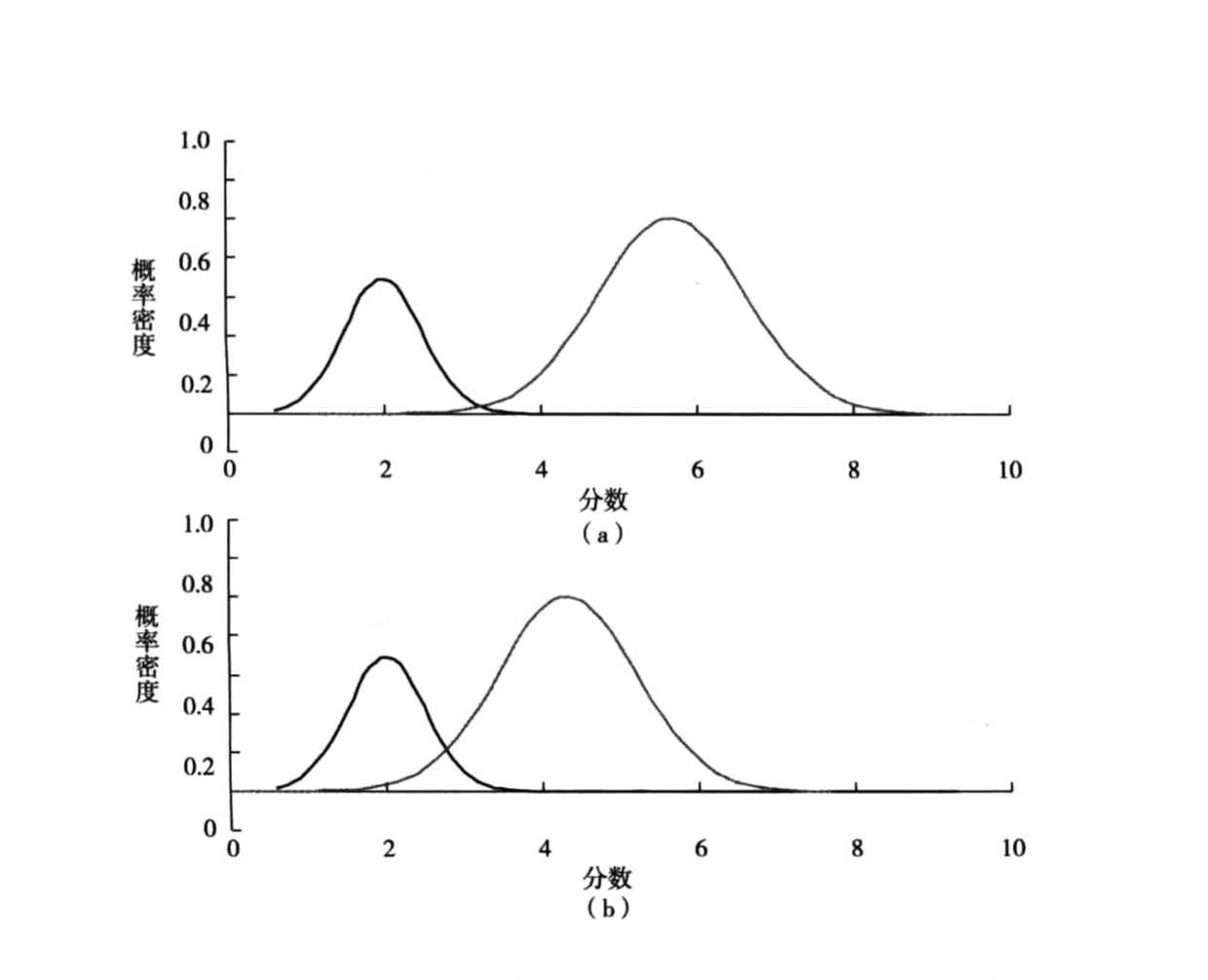
技术分享图片

在这之前，我们先介绍一下熵的概念，这在分类算法中很常见也很有用。

2.1 信息熵

先来看一道老鼠与毒药的问题：

有100只一模一样的瓶子，编号1-100。其中99瓶是水，一瓶是看起来像水的毒药。只要老鼠喝下一小口毒药，一天后则死亡。请问最少需要几只老鼠才能在一天检验出哪个号码瓶子里是毒药？

我们可以用信息论来解决。在这个问题中，对于每一个瓶子而言，其是毒药的概率都是1/100，要完全表示所有的可能性，我们需要用

\[\log_2 100 = 6.64 <7\,\mbox{(字节)}\]

至少7个字节来存储，于是答案就是7只老鼠。这就是熵，熵是信息论中的基础，用于度量随机变量的不确定性程度。对于一般的事件 X（每种可能性发生的概率不一样），我们有：

\[H(X)=-\sum_{x\in X} p(x)\log p(x)\]

这里画了一张图，用于表示一些基本的熵以及它们之间的关系。

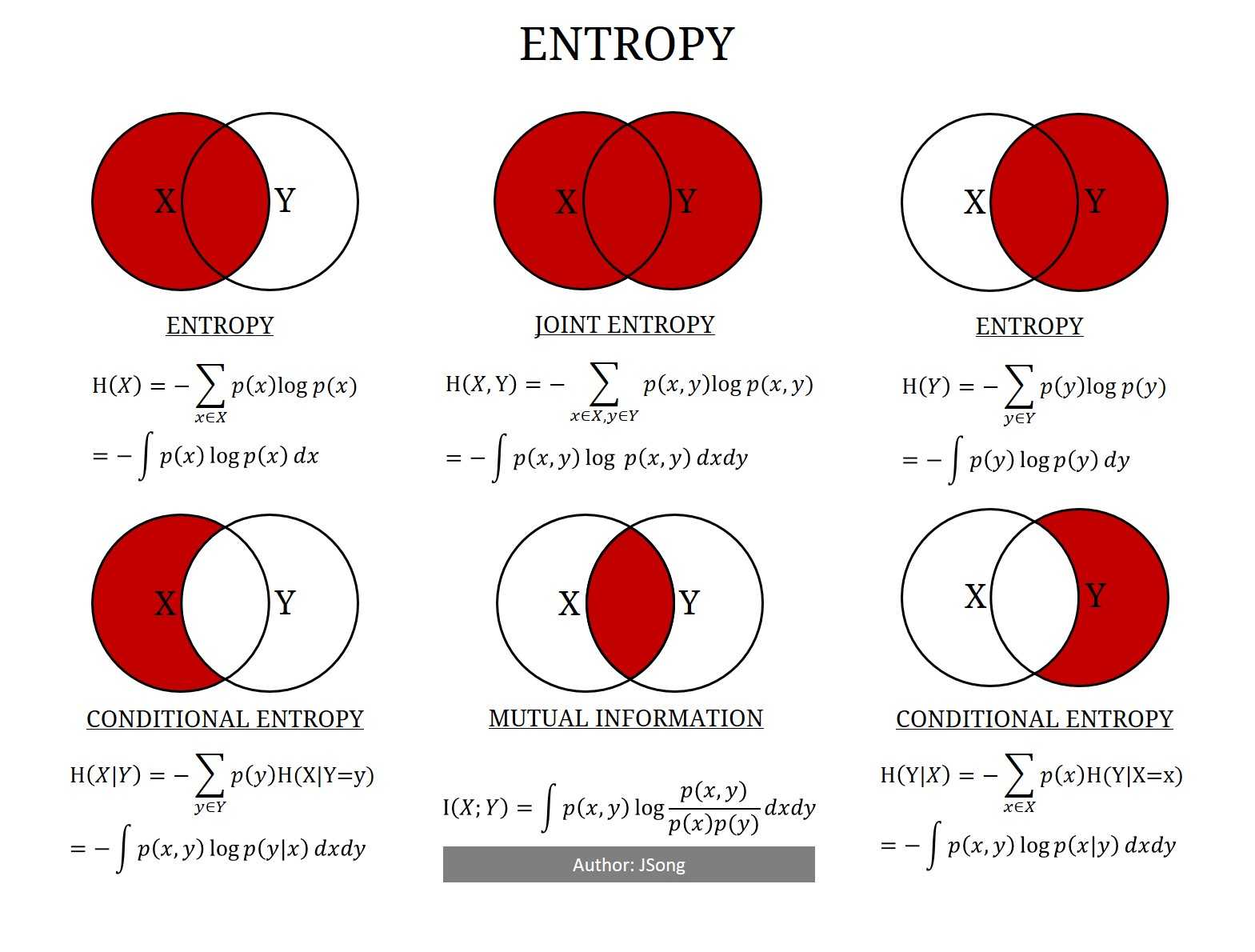
技术分享图片

从图中可以看出

\[联合熵 H(X,Y) = 熵 H(X) + 条件熵 H(Y|X)\]

\[ = 条件熵 H(X|Y) + 互信息 I(X;Y) +条件熵 H(Y|X)\]

另外除了这四种熵，比较常用的还有 相对熵 和 交叉熵 。

相对熵(K-L散度)：

相对熵是两个随机分布之间距离的度量。在统计学中，它对应的是似然比的对数期望。相对熵 D(p||q) 度量了当真实分布为 p 而假定分布为 q 时的无效性。

\[D(p||q)=\int\,p(x)\log\frac{p(x)}{q(x)}dx\]

相对熵总是非负的，注意到其并不对程，也不满足三角不等式，所以严格来讲，它并不能称为“距离”，所以实际使用中，我们可以作对称化处理：

\[D=D(p||q)+D(q||p)=\int(p(x)-q(x))\log\frac{p(x)}{q(x)}dx\]

另外一种改进方式是 JS散度（Jensen-Shannon） ：

\[JS(p||q)=\frac{1}{2}D_{KL}(p||\frac{p+q}{2})+\frac{1}{2}D_{KL}(q||\frac{p+q}{2})\]
K-L散度是一个非常不错的“距离”，在下一节我们还会继续讲这个指标，但是要注意K-L散度是无界的。

另外注意到互信息(信息增益)关于X和Y是对称的，即H(X)-H(X|Y)=H(Y)-H(Y|X)。而且它与相对熵存在如下等价关系：

\[I(X;Y)=D(\ p(x,y)||p(x)p(y)\ )\]

从该等价式可以看出，当X和Y之间几乎相互独立，即相互所包含的信息很少时，联合分布p(x,y)与乘积分布p(x)p(y)之间的K-L距离相应的也很小。

交叉熵：

假设已知随机变量的真实分布为p，预测分布为q，可以构造平均描述长度为 H ( p ) 的码。但是如果使用分布q的编码，那么在平均意义上就需要 H ( p ) + D(p||q)比特来描述这个随机变量。

\[H(p,q)=-\int\,p(x)\log\,q(x)dx=H(p)+D(p||q)\]

也就是说交叉熵度量了从q到p还需要的信息量。交叉熵常用作部分分类模型(如逻辑回归算法)的损失函数（详见文章一切从逻辑回归开始）

在我们的这个评分模型中，如果已经有了混淆矩阵，则可以直接计算相对熵：

\[D(f(s|G)||f(s|B))= \frac{11990}{12369}\cdot\log_2 \frac{11990\cdot 4813}{12369 \cdot 4373}+\frac{379}{12369}\cdot\log_2 \frac{379\cdot 4813}{12369 \cdot 440}=0.04\]

如果还没确定阈值，则有两种方法来计算连续随机变量的熵，一种是把模型输出的分数作为 f(s|G) 和 f(s|B) 两个随机分布的抽样结果，然后拟合出真实的分布，最后再用公式计算（实际算法中可以用 k近邻算法来快速近似）。另一种方法就是离散化，将信用分数划分成几个区间，然后计算信息量IV（见下一小节的介绍）。

它们的 Python 实现方法如下：

from reportgen.utils import entropy
from reportgen.utils import entropyc
from reportgen.utils import entropyd

# 基于混淆矩阵的方法
entropy.entropy(xp)#熵
# KL散度，没有对称化
entropy.kl_div(xp,yp) #此时p和q的长度得一致，且和为1
# 也可以用 scipy工具包
from scipy import stats
stats.entropy(xp) #熵
stats.entropy(xp,yp) #KL散度


# 基于信用评分，且连续化处理的方法
entropyc.entropy(xp)
# KL散度，没有对称化
entropyc.kl_div(xp,yp)

# 基于信用评分，且离散化处理的方法
entropyd.entropy(xp)
# KL散度，没有对称化
entropyd.kl_div(xp,yp)

2.2 KL 距离

我们还可以从另一个角度来推导出 KL 距离。

如果想考察预测变量区分好坏借款人的表现，我们可以用两个分布的期望之差(类似于马氏距离)：

\[\int\ s\cdot(f(s|G)-f(s|B))ds\]

然而这个差并没有考虑到某些 s 值的信息量远高于其他的情况，于是我们可以用证据权重 WOE 来替换s：

\[D_{KL}=\int\ (f(s|G)-f(s|B))\log\left(\frac{f(s|G)}{f(s|B)}\right)\,ds\]

这被称为对称化后的 K-L散度 (Kullback–Leibler divergence)，这里我们简单的称之为 KL 距离

一般情况 s 往往不是连续的，这时候我们可以把分数划分成很多个小区间来近似散度。假定有I个区间，每个区间i中有好人 \(g_i\) 个、坏人 \(b_i\) 个，且总共有 \(n_G\) 个好人和 \(n_B\) 个坏人。则我们用 \(g_i\) / \(n_G\) 代替 f(s|G)，于是KL 距离可以近似为（信息量，IV）：

\[IV=\sum_{i=1}^{I}[\frac{g_{i}}{n_G}-\frac{b_i}{n_B}]\log[\frac{g_in_B}{b_in_G}]\]

2.3 其他概率分布距离

K-L散度的不足之处在于它是无界的。事实上K-L散度属于更广泛的 f-divergence (/wiki/F-divergence) 中的一种。如果p和q被定义成空间中的两个概率分布，则 f 散度被定义为：

\[D_{f}(p||q)=\int\,f(\frac{p(x)}{q(x)})q(x)dx\]

很多常见的散度，例如 KL-divergence (/wiki/KL-divergence)、Hellinger distance (/wiki/Hellinger_distance)、和 total variation distance (/wiki/Total_variation_distance) 都是特殊的 f-divergence。下表给出了它们的对应函数关系：

技术分享图片

这其中常用的有：

卡方散度 :

\[f(t)=(t-1)^2\]

\[D_{\mathcal{X}^2}(p||q)=\int\,\frac{(p(x)-q(x))^2}{q(x)}dx\]

这正好是卡方值，其中p(x)和q(x)分别是观察频数分布和期望频数分布。

Hellinger distance ：

\[f(t)=(t^{1/2}-1)^2\]

\[D_{\mathcal{H}}^2(p||q)=\frac{1}{2}\int[\sqrt{p(x)}-\sqrt{q(x)}\ ]^2dx=1-\int\sqrt{p(x)q(x)}dx\]

用测度论来看，它就是

\[D_{\mathcal{H}}(p||q)=\frac{\sqrt{2}}{2}||\sqrt{p(x)}-\sqrt{q(x)}||_2\]

Total variation distance :

\[f(t)=\frac{|t-1|}{2} \]

\[D_{\delta}(p||q)=\frac{1}{2}\int|p(x)-q(x)|dx=\frac{1}{2}||p(x)-q(x)||_1\]

除了f-divergence，还有一些不错的距离：

巴氏距离 （Bhattacharyya Distance）：

\[D_{\mathcal{B}}(p||q)=-\log\ [\int\sqrt{p(x)q(x)}dx]\]

仔细观察，会发现，相对于Hellinger distance，Bhattacharyya Distance就是用ln(x) 替换x-1而已

MMD 距离 （Maximum mean discrepancy)。MMD 距离即最大均值差异，度量在再生希尔伯特空间中两个分布的距离，是一种核学习方法。两个随机变量的距离为
Wasserstein distance 。详见 /wiki/Wasserstein_metric

2.4 马氏距离

马氏量比较简单，它就是两个概率密度函数的众数之差/标准差

\[D_M=|\frac{\mu_G-\mu_B}{\sigma}|\]

当好人和坏人的分布是正态分布且方差相等时，有

\[D=D_M^2\]

2.5 卡方距离

设N为样本数，fo和fe分别为观察频数和期望频数：

\[fo=Pr(x=x_i,y=y_i)\cdot\,N\]
\[fe=Pr(x=x_i)\cdot\,Pr(x=y_j)\cdot\,N\]

则卡方距离(卡方统计量) 可以定义为：

\[\mathcal{X}^2=\sum_{i,j}\frac{(fo-fe)^2}{fe}\]

注意到上式的最右边等价于：

\[\frac{(fo-fe)^2}{fe}=(fo-fe)\times(\frac{fo}{fe}-1)\]

而fo/N可以看成是联合分布的概率，fe/N可以看成是乘积分布的概率，又

\[fo/fe-1\approx\log(fo/fe)\]

所有我们有

\[\frac{\mathcal{X}^2}{N}=\int[p(x,y)-p(x)p(y)]\times[\frac{p(x,y)}{p(x)p(y)}-1]dxdy\approx\,D\]

从这个角度来看，卡方距离是联合分布与乘积分布之间的相对熵的一种近似，也有点类似于互信息。

# reportgen
from reportgen.utils import chi2
chi2(X,y) # X可以是 DataFrame 数据，多个特征
# scipy
from scipy import stats
stats.chi2_contingency(fo)

3、基于随机变量分布函数的评估

散度与其相关的统计量都是为了两个随机分布的密度函数之间的差异。这一节我们则介绍它们分布函数之间的差异。

3.1 KS 统计量

我们将KS统计量定义如下：

\[KS=\max_{s}(F(s|B)-F(s|G))\]

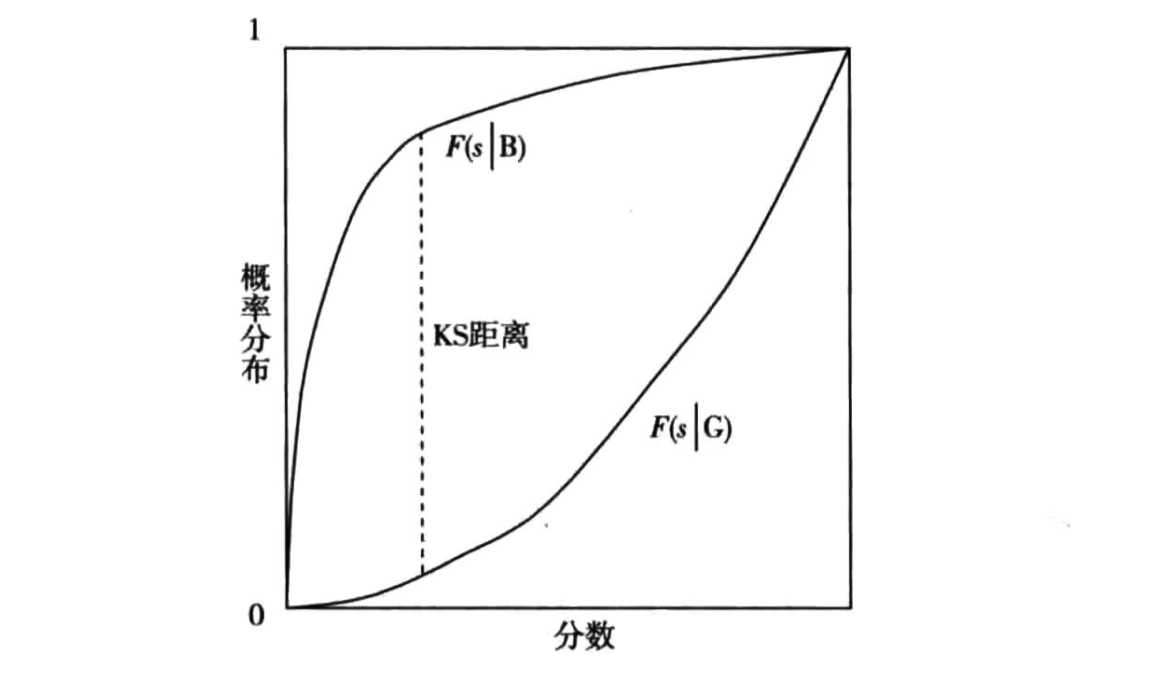
技术分享图片

KS统计量反映的判别能力没有一个确定的标准，经验上KS统计量至少要等于0.4才反应一个较好的判别能力。

KS统计量的缺点在于它描述的是在“最优区分分数”下的情形，但商业决策中需要一个相关或合适的临界分数。我们只能理解成，实际临界分数处的条件分布的距离比KS统计量小，换句话说，KS统计量仅是好坏距离或区分度的上限。

3.5 ROC (Receiver Operating Characteristi) 曲线

信用评分中最常用的判别能力的度量工具就是 ROC 曲线 和与之很相似的 CAP（Cumulative Accuracy profile）曲线。这些曲线下方的区域引出了两种判别能力的度量：Gini系数和准确率AR。

ROC曲线是坏人条件概率分布函数 F(s|B) 相对于好人条件概率分布函数 F(s|B) 的图形，如下图所示。

\[F(s|G)=P(S\leq\ s|G)\]

\[F(s|B)=P(S\leq\ s|B)\]

如果一个模型的判别能力完美，那么存在一个分数 s_B ，其大于所有坏人的分数且小于所有好人的分数。此时ROC曲线会经过B点，即下图中的点（0，1）。在另一种极端情形下，如果评分卡并不比随机方式更好（也就是在每一个分数点上，低于这个分数的比例与好人比例相同）,那么

\[F(s|G)=F(s|B)\]

即下图中的虚线。

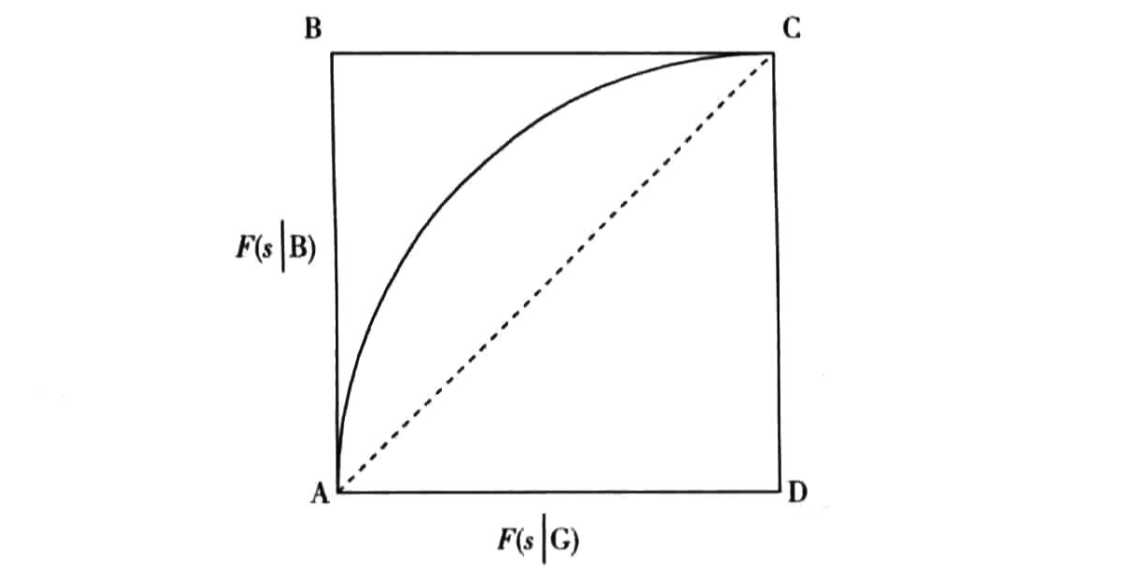
技术分享图片

ROC曲线下的面积（Area under the ROC curve，简称AUROC或者AUC）可评价判别能力的大小。一般评分卡的AUROC通常介于 0.5~1 之间，且面积越大，判别能力越好。

\[\text{AUROC}=\int\ F(s|B)dF(s|G)=\int\ F(s|B)f(s|G)ds\]

有时候我们更倾向于用范围0到1来标准化测量结果，0代表完全随机，1代表完美随机能力。此时我们可以将 AUROC 转换成 Gini 系数，其等于 ROC 曲线与对角线之间面积的两倍。

\[\text{GINI}=2\text{AUROC}-1=2\int(F(s|B)-F(s|G))dF(s|G))\]

每个分数在ROC曲线上的点（F(s|G)，F(s|B)），该点垂直投射到对角线上的点的横纵坐标相等。所以曲线上这点的垂直距离变成了 |F(s|B)-F(s|G)|。很明显

KS统计量就是这个距离的最大值

而 Gini系数 (/wiki/Gini_coefficient)是这个距离在整个曲线上积分的两倍，因此 GINI<2KS。另外可以证明GINI>KS，如果进一步放缩GINI系数，还可以证明GINI<2KS-(KS)^2，于是我们有：

\[\text{KS}<\text{GINI}<2\text{KS}-(\text{KS})^2\]

注1：基于混淆矩阵定义的 ROC 曲线

在很多机器学习的书中，ROC曲线是通过混淆矩阵来定义的，纵轴是 真正率（True Positive Rate，正样本中预测为正的比例），横轴是 假正率 (False Positive Rate,负样本中预测为正的比例)：

\[TPR=\frac{TP}{TP+FN}\]

\[FPR=\frac{FP}{TN+FP}\]

可以证明，该定义本质上与上述基于密度函数的定义是等价的。

当给定阈值 s_c 后，分数大于 s_c 时，模型判定为好人，当分数小于 s_c 时，模型判定为坏人。。我们可以用分布函数重绘混淆矩阵（差一个总样本数），如下图

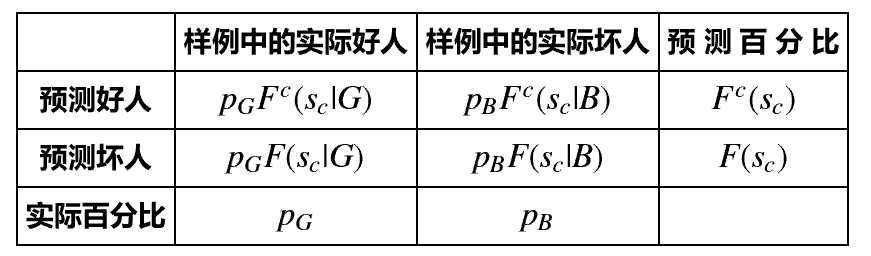
技术分享图片

此时可以看出真正率 TPR=F(s|B)，假正率 FPR=F(s|G)。

注2：ROC曲线的绘制

在画ROC曲线和计算Gini系数时，分值大小并不重要，真正重要的是这些人分数的相对排序。将分数按升序排列，得到BGBBGGBGGG·······。依次将前n个样本预测为B即可得到ROC曲线。

它们的 python 实现方法如下：

from sklearn.metrics import roc_curve,auc
import matplotlib.pyplot as plt
fpr, tpr, thresholds=roc_curve(y,y_proba)
auc_score=auc(fpr,tpr)
fig,ax=plt.subplots()
ax.plot(fpr,tpr,label=‘AUC=%.5f‘%auc_score)
ax.set_title(‘Receiver Operating Characteristic‘)
ax.plot([0, 1], [0, 1], ‘--‘, color=(0.6, 0.6, 0.6))
ax.legend()
fig.show()

3.6 CAP曲线

在市场营销文献中，有一个和 ROC 曲线很类似的方法叫做累积准确性（cumulative accuracy profile，CAP），或者成为 提升曲线 （lift curve）。与ROC曲线不同，它的横纵坐标不是 F(s|G) 和 F(s|B)，而是 F(s) 和 F(s|B)。所以横坐标表示的是总体被拒绝的比例，纵坐标表示好人被拒绝的比例。

完美判别评分卡的 CAP 曲线会经过 B ( p_B, 1)点，其中 p_B 是总体中坏人的比例。

就像ROC曲线和Gini系数一样，曲线到对角线的面积与完美判别到随机判别面积的比例可以整合CAP曲线包含的信息。这个比例成为准确率（accuracy rate，AR）

\[\text{AR}=\frac{2}{1-p_B}(\int(F(s|B)f(s)ds-0.5))\]

可以证明AR=GINI，但两个曲线并不一样。ROC曲线不需要指导原始总体的分布，而只看评分卡本身。但CAP曲线包含了总体的信息，随总体变化而变化。

4、性能度量的实验估计方法

一个分类学习器最主要的目的在于预测新样本，所以更多的应该考虑它的泛化误差。无论是哪种评价指标，我们都应该应用在不同于训练样本之外的数据集上。

选择一个能在一定评判准则 L 下达到最优的函数：可以是似然函数，也可以是 MSE，还可以是 F1 值、散度等各种评估指标。再选择一个评分函数 s_D( ) 使得：

\[\max_{s\in\ s_D}\mathcal{L}(s|D)=\mathcal{L}(s_D|D)\]

我们需要找到在样本上使得测量指标最大化的分类学习器。为了得到无偏估计，我们必须考察其在保留样本或检验样本上的表现。通常我们会有足够充分的数据建立分类学习器，能够将数据分成训练样本和检验样本。否则，我们只能用一些标准的统计学习方法如交叉验证或 bootstrap 法来获得无偏估计。

注：当样本不足够充分时，D只能当成总体的一个抽样。此时通过交叉验证或者bootstrap法可以有效降低模型的泛化方差，同时也能充分利用好每一个数据，毕竟都来之不易。

4.1 留出法

"留出法 " 将数据集D划分成两部分，一部分为训练集：train_set，另一部分为测试集：test_set. 测试集不参与模型的训练，仅用于计算模型的泛化误差。一般来讲，训练集的占比为
2/3-4/5.

留出法常用于比较多个分类模型的泛化误差能力，当我们要更好的估计单个分类模型的泛化误差时，特殊的，可以用 "留一法" 。即建立 |D| 个分类模型，其中每一个分类模型的测试集仅有一个。

4.2 交叉验证法

如k-fold，形成k个模型，将模型的平均值作为最终的分类结果

\[\frac{\sum_{r=1}^{N}\mathcal{L}(s_{D^{c}_{r}}|D_{r})}{N}\]

4.3 bootstrap法

每次有放回的抽样|D|个样本，这样大概有

\[\ln(1-\frac{1}{|D|})^{|D|}\approx\frac{1}{e}=0.368\]

的样本不会被抽中，可以将他们作为测试集。

\[\mathcal{L}(s_{D}|\mathcal{V})\approx\mathcal{L}(s_{D}|\mathcal{D})-\frac{\sum_{r=1}^{N}\mathcal{L}(s_{B_r}|\mathcal{B_r})-\mathcal{L}(s_{B_r}|\mathcal{B_r^c})}{N}\]

考虑到只有0.632的样本用于测量误差，我们有一个更稳定的误差估计：

\[\mathcal{L}(s_{D}|\mathcal{V})\approx\sum_{r=1}0.632\mathcal{L}(s_{B_r}|\mathcal{B}_r^c)+0.368\mathcal{L}(s_{B_r}|\mathcal{B}_r)\]

python 实现方式如下:

from sklearn.linear_model import LogisticRegressionCV
from sklearn.model_selection import cross_val_score
lr = LogisticRegressionCV()
print(cross_val_score(lr, X, y,cv=10).mean())
#>>>0.7245