期望得分:100+100+40=240
实际得分:100+100+20=220
T1

sum[r]^sum[l-1]<k
对前缀异或和建trie树
假设当前是第i位,sum[r]的地i位是l
如果k的第i位为1,累加l,当前指针转到sum[r]的l^1
否则,当前指针直接转到sum[r]的l

#include<cstdio> #include<iostream> using namespace std; typedef long long LL; #define N 100001 int bit[31]; int tr[N*30][2],sum[N*30]; int k; int tot=1,root=1; LL ans; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void insert(int x) { int now=root; bool j; for(int i=30;i>=0;--i) { j=x&bit[i]; if(!tr[now][j]) tr[now][j]=++tot; now=tr[now][j]; sum[now]++; } } void query(int x) { int now=root; bool l,r; for(int i=30;i>=0;--i) { if(!now) return; l=x&bit[i]; r=l^1; if(k&bit[i]) { ans+=sum[tr[now][l]]; now=tr[now][r]; } else now=tr[now][l]; } } int main() { freopen("bit.in","r",stdin); freopen("bit.out","w",stdout); bit[0]=1; for(int i=1;i<=30;++i) bit[i]=bit[i-1]<<1; int n,x; read(n); read(k); insert(0); int pre=0; for(int i=1;i<=n;++i) { read(x); pre^=x; query(pre); insert(pre); } cout<<ans; }
T2

线段树
设sum[i]表示区间的和,sum2[i]表示区间数的平方和
预处理pre1[i]:i^2的前缀和,pre2[i]:i*2的前缀和
现在要对区间加首项为a1,公差为d的等差数列
假设区间有4个数,A、B、C、D,区间大小siz=4
原来的sum[i]=A+B+C+D
现在的sum[i]=A+a1+B+a1+d+C+a1+2d+D+a1+3d
即新的sum[i]=原来的sum[i]+siz*a1+(siz-1)*siz*d
原来的sum2[i]=A^2+B^2+C^2+D^2
现在的sum2[i]=(A+a1)^2 + (B+a1+d)^2 + (C+a1+2d)^2 + (D+a1+3d)^2
=A^2+a1^2+2*A*a1 + B^2+a1^2+d^2+2*B*a1+2*B*d+2*a1*d + C^2+a1^2+4*d^2+2*C*a1+4*C*d+4*a1*d + D^2+a1^2+9*d^2+2*D*a1+6*D*d+6*a1*d
=(A^2+B^2+C^2+D^2)+(a1^2+a1^2+a1^2+a1^2)+(d^2+4*d^2+9*d^2)+(2*A*a1+2*B*a1+2*C*a1+2*D*a1)+(2*a1*d+4*a1*d+6*a1*d)+(2*B*d+4*C*d+6*D*d)
=原来的sum2[i]+siz*a1^2+pre[siz-1]*d^2+2*原来的sum[i]*a1+pre[siz-1]*a1*d+pre[siz-1]*a1*d+ (2*B*d+4*C*d+6*D*d)
最后的那个怎么维护?
令sum3[i]表示0*A+1*B+2*C+3*D……
最后那个就是sum[3]*2*d
合并时,sum,sum2直接合并
sum3[k]=sum3[L]+sum3[R]+siz[L]*sum[R]
L:0*A+1*B+2*C
R:0*D+1*E+2*F
合并后:0*A+1*B+2*C+3*D+4*E+5*F
合并后R的部分与子区间的R每个值差了siz[L]倍

#include<cstdio> #include<iostream> using namespace std; const int mod=1000000007; #define N 100001 typedef long long LL; LL pre1[N],pre2[N]; LL siz[N<<2]; LL sum[N<<2],sum2[N<<2],sum3[N<<2]; LL fa1[N<<2],fd[N<<2]; LL ans; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void read(LL &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void pre(int n) { for(int i=1;i<=n;++i) { pre1[i]=(pre1[i-1]+i*i)%mod; pre2[i]=pre2[i-1]+i*2; pre2[i]-=pre2[i]>=mod ? mod : 0; } } void build(int k,int l,int r) { siz[k]=r-l+1; if(l==r) { read(sum[k]); sum2[k]=(sum[k]*sum[k])%mod; return; } int mid=l+r>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r); sum[k]=sum[k<<1]+sum[k<<1|1]; sum[k]-=sum[k]>=mod ? mod : 0; sum2[k]=sum2[k<<1]+sum2[k<<1|1]; sum2[k]-=sum2[k]>=mod ? mod : 0; sum3[k]=(sum3[k<<1]+siz[k<<1]*sum[k<<1|1]%mod+sum3[k<<1|1])%mod; } void insert_(int k,LL a1,LL d) { sum2[k]=(sum2[k]+a1*a1%mod*siz[k]%mod+d*d%mod*pre1[siz[k]-1]%mod+a1*d%mod*pre2[siz[k]-1]%mod+sum[k]*2*a1%mod+sum3[k]*d*2%mod)%mod; sum3[k]=(sum3[k]+siz[k]*(siz[k]-1)/2%mod*a1%mod+pre1[siz[k]-1]*d%mod)%mod; sum[k]=(sum[k]+siz[k]*a1%mod+siz[k]*(siz[k]-1)/2%mod*d%mod)%mod; fa1[k]+=a1; fa1[k]-=fa1[k]>=mod ? mod : 0; fd[k]+=d; fd[k]-=fd[k]>=mod ? mod : 0; } void down(int k,int s) { insert_(k<<1,fa1[k],fd[k]); insert_(k<<1|1,(fa1[k]+s*fd[k])%mod,fd[k]); fa1[k]=fd[k]=0; } void insert(int k,int l,int r,int opl,int opr,LL a1,LL d) { if(l>=opl && r<=opr) { insert_(k,a1,d); return; } int mid=l+r>>1; if(fa1[k] || fd[k]) down(k,mid+1-l); if(opr<=mid) insert(k<<1,l,mid,opl,opr,a1,d); else if(opl>mid) insert(k<<1|1,mid+1,r,opl,opr,a1,d); else { insert(k<<1,l,mid,opl,mid,a1,d); insert(k<<1|1,mid+1,r,mid+1,opr,(a1+(mid+1-opl)*d)%mod,d); } sum[k]=sum[k<<1]+sum[k<<1|1]; sum[k]-=sum[k]>=mod ? mod : 0; sum2[k]=sum2[k<<1]+sum2[k<<1|1]; sum2[k]-=sum2[k]>=mod ? mod : 0; sum3[k]=(sum3[k<<1]+siz[k<<1]*sum[k<<1|1]%mod+sum3[k<<1|1])%mod; } void query(int k,int l,int r,int opl,int opr,bool w) { if(l>=opl && r<=opr) { if(w) ans+=sum2[k]; else ans+=sum[k]; ans-=ans>=mod ? mod : 0; return; } int mid=l+r>>1; if(fa1[k] || fd[k]) down(k,mid+1-l); if(opl<=mid) query(k<<1,l,mid,opl,opr,w); if(opr>mid) query(k<<1|1,mid+1,r,opl,opr,w); } int main() { freopen("calculation.in","r",stdin); freopen("calculation.out","w",stdout); int n,m; read(n); read(m); pre(n); build(1,1,n); char c[3]; int l,r,b,k; while(m--) { scanf("%s",c); if(c[0]==‘A‘) { read(l); read(r); read(k); read(b); insert(1,1,n,l,r,b,k); } else { read(l); read(r); ans=0; query(1,1,n,l,r,c[0]==‘C‘); cout<<ans<<‘\n‘; } } }
T3
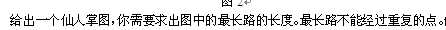
求仙人掌的直径,DP
可以去参考http://www.cnblogs.com/TheRoadToTheGold/p/7895298.html
以前做过的类似的考场上写不出来没啥好说的

#include<cstdio> #include<cstring> #include<iostream> #include<algorithm> using namespace std; #define N 100001 int front[N],to[N<<1],nxt[N<<1],val[N<<1]; int tot,ans; int low[N],dfn[N]; int fa[N],dep[N]; int dp[N]; int q[N],tmp[N<<1]; int sum[N<<1]; void read(int &x) { x=0; char c=getchar(); while(!isdigit(c)) c=getchar(); while(isdigit(c)) { x=x*10+c-‘0‘; c=getchar(); } } void clear() { tot=1; ans=0; memset(front,0,sizeof(front)); memset(dp,0,sizeof(dp)); memset(dfn,0,sizeof(dfn)); } void add(int u,int v,int w) { to[++tot]=v; nxt[tot]=front[u]; front[u]=tot; val[tot]=w; to[++tot]=u; nxt[tot]=front[v]; front[v]=tot; val[tot]=w; } void circle(int x,int y) { int cnt=dep[y]-dep[x]+1; int now=y; while(dfn[fa[now]]>=dfn[x]) tmp[cnt--]=now,now=fa[now]; tmp[cnt]=now; cnt=dep[y]-dep[x]+1; int m=cnt; for(int i=1;i<=cnt;++i) tmp[++m]=tmp[i]; for(int i=1;i<=cnt;++i) for(int j=front[tmp[i]];j;j=nxt[j]) if(to[j]==tmp[i+1]) { sum[i+1]=val[j]; break; } for(int i=2;i<=cnt;++i) sum[i+cnt]=sum[i]; for(int i=1;i<=m;++i) sum[i]+=sum[i-1]; int h=0,t=0; for(int i=1;i<=m;++i) { while(h<t && i-q[h]>=cnt) h++; if(h<t) ans=max(ans,dp[tmp[i]]+dp[tmp[q[h]]]+sum[i]-sum[q[h]]); while(h<t && dp[tmp[i]]-sum[i]>dp[tmp[q[t-1]]]-sum[q[t-1]]) t--; q[t++]=i; } for(int i=2;i<=cnt;++i) dp[x]=max(dp[x],dp[tmp[i]]+max(sum[i],sum[cnt+1]-sum[i])); } void tarjan(int x,int y) { dfn[x]=low[x]=++tot; for(int i=front[x];i;i=nxt[i]) { if(y==(i^1)) continue; if(!dfn[to[i]]) { fa[to[i]]=x; dep[to[i]]=dep[x]+1; tarjan(to[i],i); low[x]=min(low[x],low[to[i]]); } else low[x]=min(low[x],dfn[to[i]]); if(low[to[i]]>dfn[x]) { ans=max(ans,dp[x]+dp[to[i]]+val[i]); dp[x]=max(dp[x],dp[to[i]]+val[i]); } } for(int i=front[x];i;i=nxt[i]) if(fa[to[i]]!=x && dfn[x]<dfn[to[i]]) circle(x,to[i]); } int main() { freopen("path.in","r",stdin); freopen("path.out","w",stdout); int T; int n,m; int u,v,w; read(T); while(T--) { clear(); read(n); read(m); while(m--) { read(u); read(v); read(w); add(u,v,w); } tot=0; tarjan(1,0); cout<<ans<<‘\n‘; } }
Summary
1、5个小时的时间,可以放心大胆的去写思路清晰的正解
2、A掉题远比暴力带来的收益多,无论是分数还是心理
3、一定要写对拍,今天如果没写对拍估计分数两位数
4、一定要读好题,尤其是输入描述中先输入啥后输入啥,像这种:“A l r k b:在区间[l,r]上加上一个首项为b、公差为k的等差数列。”,今天就读成了A l r b k,白白浪费了半个小时
5、当出现小数据正确,大数据错误时,去检查数组大小,今天T2的线段树一个数组没开4倍,又浪费了半小时
6、要给不打算写正解的题留出充足的暴力时间,如今天的T3,至少50分的暴力因为时间原因写了40,得了20
7、最后一道题,有正解思路但细节问题还没想好,不成熟,还剩不到一小时,果断选择写暴力,就像T3,如果不自量力选择去写正解,20分都没有了
8、正常发挥,会的分都拿到,名次一定差不了。今天期望240(rank2),实际220(rank2),很多实力比我强的各种写炸。
9、所以,将自己的实力在规定的时间、地点全部发挥出来,不留遗憾才是我现在要做的!

