Puzzle

    A children‘s puzzle that was popular 30 years ago consisted of a 5 5 frame which contained 24 small squares of equal size. A unique letter of the alphabet was printed on each small square. Since there were only 24 squares within the frame, the frame also contained an empty position which was the same size as a small square. A square could be moved into that empty position if it were immediately to the right, to the left, above, or below the empty position. The object of the puzzle was to slide squares into the empty position so that the frame displayed the letters in alphabetical order.

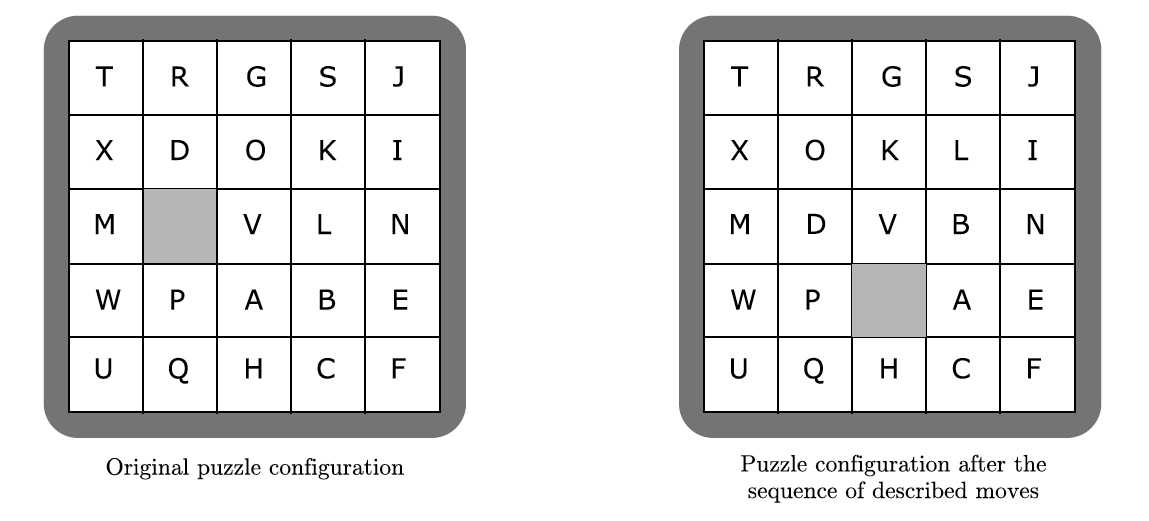
    The illustration below represents a puzzle in its original conguration and in its conguration after the following sequence of 6 moves:

1) The square above the empty position moves.

2) The square to the right of the empty position moves.

3) The square to the right of the empty position moves.

4) The square below the empty position moves.

5) The square below the empty position moves.

6) The square to the left of the empty position moves.

  Write a program to display resulting frames given their initial congurations and sequences of moves.

Input

    Input for your program consists of several puzzles. Each is described by its initial conguration and the sequence of moves on the puzzle. The rst 5 lines of each puzzle description are the starting conguration. Subsequent lines give the sequence of moves.

    The rst line of the frame display corresponds to the top line of squares in the puzzle. The other lines follow in order. The empty position in a frame is indicated by a blank. Each display line contains exactly 5 characters, beginning with the character on the leftmost square (or a blank if the leftmost square is actually the empty frame position). The display lines will correspond to a legitimate puzzle.

    The sequence of moves is represented by a sequence of As, Bs, Rs, and Ls to denote which square moves into the empty position. A denotes that the square above the empty position moves; B denotes that the square below the empty position moves; L denotes that the square to the left of the empty position moves; R denotes that the square to the right of the empty position moves. It is possible that there is an illegal move, even when it is represented by one of the 4 move characters. If an illegal move occurs, the puzzle is considered to have no nal conguration. This sequence of moves may be spread over several lines, but it always ends in the digit 0. The end of data is denoted by the character Z.

Output

    Output for each puzzle begins with an appropriately labeled number (Puzzle #1 , Puzzle #2 , etc.). If the puzzle has no nal conguration, then a message to that effect should follow. Otherwise that nal conguration should be displayed.

    Format each line for a nal conguration so that there is a single blank character between two adjacent letters. Treat the empty square the same as a letter. For example, if the blank is an interior position, then it will appear as a sequence of 3 blanks | one to separate it from the square to the left, one for the empty position itself, and one to separate it from the square to the right.

    Separate output from different puzzle records by one blank line.

    Note:  The rst record of the sample input corresponds to the puzzle illustrated above.

Sample Input

TRGSJ

XDOKI

M VLN

WPABE

UQHCF

ARRBBL0

ABCDE

FGHIJ

KLMNO

PQRS

TUVWX

AAA

LLLL0

ABCDE

FGHIJ

KLMNO

PQRS

TUVWX

AAAAABBRRRLL0

Z

Sample Output

Puzzle #1:

T R G S J

X O K L I

M D V B N

W P A E

U Q H C F

Puzzle #2:

A B C D

F G H I E

K L M N J

P Q R S O

T U V W X

Puzzle #3:

This puzzle has no final configuration.

#include <iostream>
struct coordinate {
    int row,column;
}blank,nxt;
char a[5][5],moves[1000];
bool input() {
    for (int i=0; i<5; i++) {
        gets(a[i]);
        if (a[0][0]==‘Z‘&&a[0][1]==‘\0‘)
            return false;
    }
    for (int i=0; ; i++) {
        scanf("%c",&moves[i]);
        if (moves[i]==‘\n‘&&moves[i-1]==‘0‘) break;
    }
    for (int i=0; i<5; i++) {
        for (int j=0; j<5; j++) {
            if (a[i][j]==‘ ‘||a[i][j]==‘\0‘) {
                blank.row=i;
                blank.column=j;
                break;
            }
        }
    }
    return true;
}
bool solve() {
    for (int i=0; moves[i]!=‘0‘; i++) {
        nxt=blank;
        switch (moves[i]) {
            case ‘A‘:
                nxt.row=blank.row-1;
                break;
            case ‘B‘:
                nxt.row=blank.row+1;
                break;
            case ‘L‘:
                nxt.column=blank.column-1;
                break;
            case ‘R‘:
                nxt.column=blank.column+1;
                break;
        }
        if (nxt.row<0||nxt.row>4||nxt.column<0||nxt.column>4)
            return false;
        a[blank.row][blank.column]=a[nxt.row][nxt.column];
        blank=nxt;
    }
    a[blank.row][blank.column]=‘ ‘;
    return true;
}
int main() {
    int t=1;
    while (1) {
        if (!input()) break;
        if (t!=1) printf("\n");
        printf("Puzzle #%d:\n",t++);
        if (solve()) {
            for (int i=0; i<5; i++) {
                for (int j=0; j<5; j++) {
                    printf("%c",a[i][j]);
                    if (j!=4) printf(" ");
                }
                printf("\n");
            }
        }
        else printf("This puzzle has no final configuration.\n");
    }
}