线性规划问题
MATLAB的标准形式:
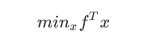
举个栗子吧:

f = [-2;-3;5]; a = [-2 5 -1;1 3 1]; b = [-10;12]; aeq = [1 1 1]; beq = 7; ? [x,y] = linprog(f,a,b,aeq,beq,zeros(3,1)); y = -y; ? % 最优解 x = 6.4286 0.5714 0.0000 y = 14.5714
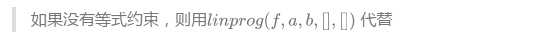
线性规划变形
(带上绝对值咯):
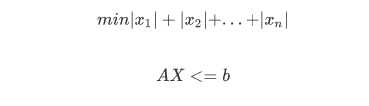
的确很复杂,不能直接用MATLAB直接计算(Lingo完全OK),需要对其进行数学变换:
理论:对于任意的?,可以写成:
? 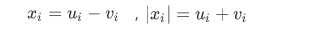
原来的目标函数就变成了:
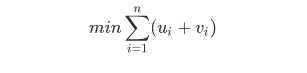
不等式就变成了:
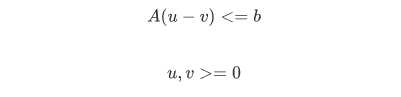
嘿嘿,现在就可以建立矩阵了,举个栗子P4:
clc,clear c = 1:4; c = [c‘,c‘]; a = [1 -1 -1 1 1 -1 1 -3 1 -1 -2 3]; a = [a,-a]; b = [-2 -1 -1/2]‘; ? [y,z] = linprog(c,a,b,[],[],zeros(4,2)); x = y(1:4)-y(5:end);
是不是和书上的程序有点不同,对的,我是完全按照这个式子写的,对于原来的目标函数写一列,但是对于矩阵乘法来说,不是看有多少列吗? 刚好这里是? 扩充矩阵? ,同理? 也是扩充为?
但是求出来的 y 很伤心却还是1维向量,却不是我想要的? 矩阵,转换一下。
当然也可以像书上的那样,令u,v 的顺序,只要不等式还是原来的不等式就行,然后转为你需要的答案即可。
