A、B、C

略

D（dfs+强连通分量）

题意：

　　给出一个n(n<=500)点m(m<=100000)边的有向图，问能否通过删去一条边使得该图无环。

分析：

　　最简单的想法就是枚举一条边删去然后判断图是否有环，这样是O(m^2)的不能接受

　　仔细想想，如果图中环数<=1，则YES；如果图中环数>=2，那么只有当它们的交恰好是一条边时，才是YES，其它情况都是NO

　　所以我们首先可以通过dfs找到一个环（vis[u]=0,1,2分别表示点u没遍历到、遍历到了在栈里、遍历过了已经出栈了），然后枚举环上的边进行删除，然后判断剩余的图中是否有环即可

　　这样时间复杂度是O(n(n+m))的

　　至于判断是否有环，我们可以求强连通分量的数目，用bitset去优化，那么时间复杂度就是O(n*n*n/64)

E（离散化+线段树）

略

F（套路+并查集）

题意：

　　给你一个树(n<=2e6)，每个点都有自己的点权，I(x,y)表示x与y路径之间的所有点最大值与最小值的差，求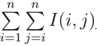

分析：

　　将最大值与最小值分别计算，以最大值为例，即计算对于每个点u，有多少个点对过u并且以v[u]为最大值

　　这就是将序列上的经典问题推广到树上来，原来的序列上的这个问题我是用set做的，但这种方法不能推广到树上来

　　其实序列上的该问题还有一个套路，就是从小到大往对应位置上加，那么对于现在刚加入的x，能凑成区间包含他作为最大值的一定是x左边连续存在的点和x右边连续存在的点，这我们可以用并查集来维护

　　推广到树上，现在从小到大加入x，那么能过x的点对一定是在x周围那些连续存在的点里面挑，这也可以用并查集来完成，不断把x的集合与四周相邻点的集合merge就行了

 1 void merge(int x,int y,int value)
 2 {
 3     if(!f[x]||!f[y]) return;
 4     x=find(x),y=find(y);
 5     s+=1LL*sz[x]*sz[y]*value;
 6     f[x]=y;
 7     sz[y]+=sz[x];
 8 }
 9 long long solve()
10 {
11     for(int i=1;i<=n;++i) pos[i]=i;
12     sort(pos+1,pos+n+1,cmp);
13     for(int i=0;i<=n;++i) f[i]=0,sz[i]=0;
14     s=0;
15     for(int i=1;i<=n;++i)
16     {
17         int x=pos[i];
18         f[x]=x,sz[x]=1;
19         for(int j=0;j<g[x].size();++j) merge(x,g[x][j],a[x]);
20     }
21     return s;
22 }

View Code

G（莫比乌斯反演）

题意：

　　给定一个n和k（均不超过2e6），定义b(i)表示gcd(a1,a2,...,an)=1的序列个数，其中1<=ai<=i，现在要求出b(1) b(2) ... b(k)

分析：

　　我们先确定上界i，那么F(x)表示gcd是x倍数的序列个数，f(x)表示gcd是x的序列个数

　　显然F(x)=[i/x]^n

　　那么有F(d)=Σf(n) (d|n) ，反演一下有f(d)=Σμ(n/d)F(n) (d|n)

　　那么b(i)=f(1)=Σμ(j)F(j) (1<=j<=i)

　　那么对于确定上界i，我们就通过莫比乌斯反演求出了b(i)的值，但我们现在要求出所有的b(1) .. b(k)

　　我们考察相邻的b(i-1)和b(i)，发现[i/x]^n和[(i-1)/x]^n不一样当且仅当i是n的因数

　　于是我们可以枚举因数，做出每一项与前一项的差值，然后求个前缀和就可以得到每一个b(i)了

　　时间复杂度O(klogk)