其实所谓的蒙特卡洛法就是我们的随机化算法啊,最简单的应用就是撒豆子求面积了。
那就举两个栗子,一个就是撒豆子,一个是非线性整数规划问题。
撒豆子
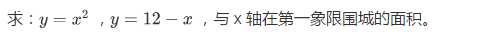
clc,clear x = unifrnd(0,12,[1,1e7]); y = unifrnd(0,9,[1,1e7]); ? cnt = sum(y<x.^2&x<=3) + sum(y<12-x&x>=3); s = 12*9*cnt/1e7;
非线性整数规划
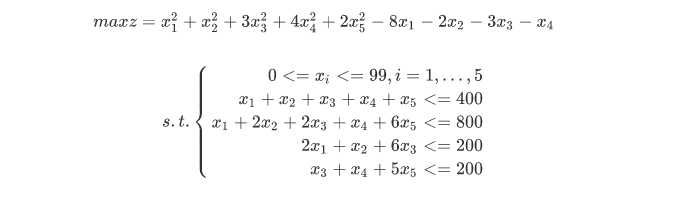
可以算一个概率,假设目标函数落在高值区域的概率为? 、? ,则当枚举? 个点后,至少有一个点能落在高值区域的概率为:
?
% mente.m function [f,g] = mente(x) f = x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5); g = [sum(x)-400 x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800 2*x(1)+x(2)+6*x(3)-200 x(3)+x(4)+5*x(5)-200]; % test.m rand(‘state‘,sum(clock)); p0 = 0; tic for i = 1:10^6 x = randi([0,99],1,5); [f,g] = mente(x); if all(g<=0) if p0<f x0 = x; p0 = f; end end end toc
