Acknowledgement to Stanford CS229.
Generative modeling is itself a kind of unsupervised learning task[1]. Given unlabelled data,

To estimate the parameters, we can write the likelihood as
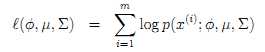
which is also
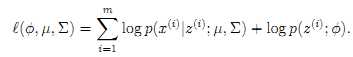
The EM algorithm can solve this pdf estimation iteratively.




An example is provided here. The data points are drawn from 2 gaussian distributions.
1 import numpy as np 2 import operator 3 np.random.seed(0) 4 x0=np.random.normal(0,1,50) 5 x0=np.concatenate((x0,np.random.normal(2,1,50)), 6 axis=0) 7 8 mus0=np.array([ 9 0,1 10 ]) 11 sigmas0=np.array([ 12 2,2 13 ]) 14 def gauss(x,mu,sigma): 15 """ 16 17 :param x: 18 :param mu: 19 :param sigma: 20 :return: pdf(x) 21 """ 22 # if np.abs((x-mu)/sigma)<1e-5: 23 # return 24 # numerator=np.exp( 25 # -(x-mu)**2/(2*sigma**2) 26 # ) 27 numerator=np.exp( 28 -0.5*((x-mu)/sigma)**2 29 ) 30 denominator=np.sqrt(2*np.pi*sigma**2) 31 return numerator/denominator 32 def e_step(mus=mus0,sigmas=sigmas0,x=x0,priors=np.ones(len(mus0))/len(mus0)): 33 """ 34 35 :param mus: gaussian centers, an array of shape (m,) 36 :param sigmas: gaussian standard deviations, an array of shape (m,) 37 :param x: n samples with no labels 38 :return: m by n array, where m is # classes 39 """ 40 assert len(mus)==len(sigmas),"mus and sigmas doesn‘t have the same length" 41 m=len(mus) 42 n=len(x) 43 w=np.zeros(shape=(m,n)) 44 for j in range(m): 45 for i in range(n): 46 w[j][i]=gauss(x=x[i],mu=mus[j],sigma=sigmas[j])*priors[j] 47 w_sum_wrt_j=np.sum(w,axis=0)#note j is the row index 48 for j in range(m): 49 w[j,:]=w[j,:]/w_sum_wrt_j 50 return w 51 def m_step(w,current_mus,x=x0): 52 """ 53 54 :param w: m by n array, where m is # classes 55 :return: mus: gaussian centers, an array of shape (m,) 56 sigmas: gaussian standard deviations, an array of shape (m,) 57 """ 58 m,n=w.shape 59 mus=np.zeros(shape=(m)) 60 sigmas=np.zeros(shape=(m)) 61 for j in range(m): 62 mus[j]=np.dot( 63 w[j,:],x 64 ) 65 mus/=np.sum(w,axis=1) 66 for j in range(m): 67 sigmas[j]=np.sqrt(np.dot( 68 w[j, :], (x-current_mus[j])**2 69 )) 70 sigmas/=np.sqrt(np.sum(w,axis=1)) 71 72 priors=np.zeros(shape=(len(mus))) 73 for i in range(n): 74 tmp=list(map( 75 gauss,[x[i]]*m,mus,sigmas 76 )) 77 tmpmaxindex,tmpmax=max( 78 enumerate(tmp),key=operator.itemgetter(1) 79 ) 80 # print(tmp) 81 # print(tmpmaxindex) 82 priors[tmpmaxindex]+=1/n 83 return mus,sigmas,priors 84 def solve(x=x0,priors=np.ones(len(mus0))/len(mus0)): 85 # print("priors={}".format(priors)) 86 mus=mus0 87 sigmas=sigmas0 88 for k in range(500): 89 w=e_step(mus=mus,sigmas=sigmas,x=x,priors=priors) 90 mus,sigmas,priors=m_step(w,current_mus=mus,x=x0) 91 print("k={},mus={},sigmas={},priors={}".format(k,mus,sigmas,priors)) 92 93 if __name__ == ‘__main__‘: 94 solve()
After 100 iterations, we get an approximation of the real model.
1 /usr/local/bin/python3.5 /home/csdl/review/fulcrum/gmm/gmm.py 2 k=0,mus=[ 0.81734343 1.27122747],sigmas=[ 1.60216343 1.33905931],priors=[ 0.32 0.68] 3 k=1,mus=[ 0.73393663 1.21263431],sigmas=[ 1.48989073 1.27140643],priors=[ 0.35 0.65] 4 k=2,mus=[ 0.72025041 1.24207148],sigmas=[ 1.47760392 1.25840835],priors=[ 0.36 0.64] 5 k=3,mus=[ 0.69405554 1.2656654 ],sigmas=[ 1.47453155 1.2480128 ],priors=[ 0.36 0.64] 6 k=4,mus=[ 0.65993336 1.28545741],sigmas=[ 1.47454151 1.238417 ],priors=[ 0.36 0.64] 7 k=5,mus=[ 0.62512005 1.30527053],sigmas=[ 1.4739642 1.22830782],priors=[ 0.36 0.64] 8 k=6,mus=[ 0.59009448 1.32522573],sigmas=[ 1.47230468 1.21788024],priors=[ 0.36 0.64] 9 k=7,mus=[ 0.55504913 1.34523959],sigmas=[ 1.46932309 1.20732602],priors=[ 0.36 0.64] 10 k=8,mus=[ 0.52016003 1.36521637],sigmas=[ 1.46489424 1.19678812],priors=[ 0.36 0.64] 11 k=9,mus=[ 0.4855794 1.38507002],sigmas=[ 1.45897578 1.18636451],priors=[ 0.36 0.64] 12 k=10,mus=[ 0.45142496 1.4047313 ],sigmas=[ 1.45158393 1.17611449],priors=[ 0.36 0.64] 13 k=11,mus=[ 0.41777707 1.42414967],sigmas=[ 1.44277296 1.16606539],priors=[ 0.36 0.64] 14 k=12,mus=[ 0.38468177 1.44329208],sigmas=[ 1.43261873 1.15621962],priors=[ 0.37 0.63] 15 k=13,mus=[ 0.36595587 1.46867892],sigmas=[ 1.41990091 1.14409883],priors=[ 0.37 0.63] 16 k=14,mus=[ 0.33654056 1.48870368],sigmas=[ 1.4082571 1.13343039],priors=[ 0.37 0.63] 17 k=15,mus=[ 0.30597566 1.50763142],sigmas=[ 1.39543174 1.12335036],priors=[ 0.37 0.63] 18 k=16,mus=[ 0.27568252 1.52609593],sigmas=[ 1.38137316 1.11360905],priors=[ 0.37 0.63] 19 k=17,mus=[ 0.24588996 1.54419117],sigmas=[ 1.36625212 1.10407072],priors=[ 0.37 0.63] 20 k=18,mus=[ 0.21664299 1.56192385],sigmas=[ 1.35022455 1.09464684],priors=[ 0.37 0.63] 21 k=19,mus=[ 0.18796432 1.57928065],sigmas=[ 1.33342219 1.0852798 ],priors=[ 0.37 0.63] 22 k=20,mus=[ 0.1598861 1.59623644],sigmas=[ 1.31596643 1.07593506],priors=[ 0.37 0.63] 23 k=21,mus=[ 0.13245872 1.61275414],sigmas=[ 1.2979812 1.06659735],priors=[ 0.39 0.61] 24 k=22,mus=[ 0.13549936 1.64420575],sigmas=[ 1.28163006 1.05238461],priors=[ 0.4 0.6] 25 k=23,mus=[ 0.13362832 1.67212388],sigmas=[ 1.26763647 1.03761078],priors=[ 0.4 0.6] 26 k=24,mus=[ 0.11750175 1.69125511],sigmas=[ 1.25330002 1.02525138],priors=[ 0.41 0.59] 27 k=25,mus=[ 0.11224826 1.71494289],sigmas=[ 1.23950504 1.01230038],priors=[ 0.42 0.58] 28 k=26,mus=[ 0.11153847 1.7395662 ],sigmas=[ 1.22728752 0.99889453],priors=[ 0.42 0.58] 29 k=27,mus=[ 0.0999276 1.75644918],sigmas=[ 1.21474604 0.98770556],priors=[ 0.43 0.57] 30 k=28,mus=[ 0.09911993 1.77770261],sigmas=[ 1.20375615 0.97601043],priors=[ 0.43 0.57] 31 k=29,mus=[ 0.08991339 1.79234269],sigmas=[ 1.19274093 0.96620904],priors=[ 0.43 0.57] 32 k=30,mus=[ 0.07854133 1.80401995],sigmas=[ 1.18163507 0.95803992],priors=[ 0.43 0.57] 33 k=31,mus=[ 0.06708472 1.81391145],sigmas=[ 1.1708709 0.9510143],priors=[ 0.43 0.57] 34 k=32,mus=[ 0.05629168 1.82248392],sigmas=[ 1.16077864 0.94483468],priors=[ 0.43 0.57] 35 k=33,mus=[ 0.04644144 1.8299628 ],sigmas=[ 1.15153082 0.93934709],priors=[ 0.43 0.57] 36 k=34,mus=[ 0.03761987 1.83648519],sigmas=[ 1.14319449 0.93447086],priors=[ 0.43 0.57] 37 k=35,mus=[ 0.02982246 1.84215374],sigmas=[ 1.13577403 0.93015559],priors=[ 0.43 0.57] 38 k=36,mus=[ 0.02299928 1.84705693],sigmas=[ 1.12923679 0.92636035],priors=[ 0.43 0.57] 39 k=37,mus=[ 0.01707735 1.85127645],sigmas=[ 1.12352817 0.92304533],priors=[ 0.43 0.57] 40 k=38,mus=[ 0.01197298 1.85488949],sigmas=[ 1.11858109 0.92016939],priors=[ 0.43 0.57] 41 k=39,mus=[ 0.00759925 1.85796875],sigmas=[ 1.11432244 0.91769023],priors=[ 0.43 0.57] 42 k=40,mus=[ 0.00387068 1.86058202],sigmas=[ 1.11067765 0.91556544],priors=[ 0.43 0.57] 43 k=41,mus=[ 7.06082311e-04 1.86279150e+00],sigmas=[ 1.10757393 0.91375369],priors=[ 0.43 0.57] 44 k=42,mus=[-0.00196965 1.86465346],sigmas=[ 1.10494246 0.91221583],priors=[ 0.43 0.57] 45 k=43,mus=[-0.00422464 1.86621814],sigmas=[ 1.10271971 0.91091554],priors=[ 0.43 0.57] 46 k=44,mus=[-0.00611974 1.86752982],sigmas=[ 1.10084819 0.9098198 ],priors=[ 0.43 0.57] 47 k=45,mus=[-0.00770859 1.86862714],sigmas=[ 1.09927671 0.90889909],priors=[ 0.43 0.57] 48 k=46,mus=[-0.00903796 1.86954354],sigmas=[ 1.09796019 0.90812732],priors=[ 0.43 0.57] 49 k=47,mus=[-0.01014832 1.87030773],sigmas=[ 1.09685943 0.90748172],priors=[ 0.43 0.57] 50 k=48,mus=[-0.01107441 1.87094421],sigmas=[ 1.09594057 0.90694261],priors=[ 0.43 0.57] 51 k=49,mus=[-0.01184586 1.87147378],sigmas=[ 1.09517461 0.90649307],priors=[ 0.43 0.57] 52 k=50,mus=[-0.01248783 1.87191401],sigmas=[ 1.09453685 0.90611867],priors=[ 0.43 0.57] 53 k=51,mus=[-0.01302159 1.87227973],sigmas=[ 1.09400634 0.90580718],priors=[ 0.43 0.57] 54 k=52,mus=[-0.01346505 1.87258336],sigmas=[ 1.09356541 0.90554823],priors=[ 0.43 0.57] 55 k=53,mus=[-0.01383328 1.87283531],sigmas=[ 1.09319917 0.90533313],priors=[ 0.43 0.57] 56 k=54,mus=[-0.01413888 1.87304431],sigmas=[ 1.09289515 0.90515454],priors=[ 0.43 0.57] 57 k=55,mus=[-0.0143924 1.87321761],sigmas=[ 1.09264288 0.90500635],priors=[ 0.43 0.57] 58 k=56,mus=[-0.01460264 1.87336127],sigmas=[ 1.09243365 0.90488343],priors=[ 0.43 0.57] 59 k=57,mus=[-0.01477693 1.87348033],sigmas=[ 1.09226016 0.9047815 ],priors=[ 0.43 0.57] 60 k=58,mus=[-0.01492139 1.87357899],sigmas=[ 1.09211635 0.90469701],priors=[ 0.43 0.57] 61 k=59,mus=[-0.0150411 1.87366073],sigmas=[ 1.09199717 0.90462698],priors=[ 0.43 0.57] 62 k=60,mus=[-0.01514028 1.87372844],sigmas=[ 1.09189842 0.90456896],priors=[ 0.43 0.57] 63 k=61,mus=[-0.01522245 1.87378452],sigmas=[ 1.09181661 0.90452088],priors=[ 0.43 0.57] 64 k=62,mus=[-0.01529051 1.87383097],sigmas=[ 1.09174884 0.90448106],priors=[ 0.43 0.57] 65 k=63,mus=[-0.01534687 1.87386944],sigmas=[ 1.0916927 0.90444807],priors=[ 0.43 0.57] 66 k=64,mus=[-0.01539356 1.87390129],sigmas=[ 1.09164621 0.90442075],priors=[ 0.43 0.57] 67 k=65,mus=[-0.01543222 1.87392767],sigmas=[ 1.09160771 0.90439813],priors=[ 0.43 0.57] 68 k=66,mus=[-0.01546423 1.87394951],sigmas=[ 1.09157583 0.90437939],priors=[ 0.43 0.57] 69 k=67,mus=[-0.01549074 1.87396759],sigmas=[ 1.09154943 0.90436388],priors=[ 0.43 0.57] 70 k=68,mus=[-0.01551269 1.87398257],sigmas=[ 1.09152757 0.90435103],priors=[ 0.43 0.57] 71 k=69,mus=[-0.01553086 1.87399496],sigmas=[ 1.09150947 0.9043404 ],priors=[ 0.43 0.57] 72 k=70,mus=[-0.0155459 1.87400523],sigmas=[ 1.09149449 0.90433159],priors=[ 0.43 0.57] 73 k=71,mus=[-0.01555836 1.87401373],sigmas=[ 1.09148208 0.9043243 ],priors=[ 0.43 0.57] 74 k=72,mus=[-0.01556868 1.87402076],sigmas=[ 1.09147181 0.90431826],priors=[ 0.43 0.57] 75 k=73,mus=[-0.01557722 1.87402659],sigmas=[ 1.0914633 0.90431327],priors=[ 0.43 0.57] 76 k=74,mus=[-0.01558428 1.87403141],sigmas=[ 1.09145626 0.90430913],priors=[ 0.43 0.57] 77 k=75,mus=[-0.01559014 1.8740354 ],sigmas=[ 1.09145043 0.9043057 ],priors=[ 0.43 0.57] 78 k=76,mus=[-0.01559498 1.87403871],sigmas=[ 1.09144561 0.90430287],priors=[ 0.43 0.57] 79 k=77,mus=[-0.01559899 1.87404144],sigmas=[ 1.09144161 0.90430052],priors=[ 0.43 0.57] 80 k=78,mus=[-0.01560232 1.87404371],sigmas=[ 1.0914383 0.90429857],priors=[ 0.43 0.57] 81 k=79,mus=[-0.01560506 1.87404558],sigmas=[ 1.09143556 0.90429696],priors=[ 0.43 0.57] 82 k=80,mus=[-0.01560734 1.87404714],sigmas=[ 1.0914333 0.90429563],priors=[ 0.43 0.57] 83 k=81,mus=[-0.01560923 1.87404842],sigmas=[ 1.09143142 0.90429453],priors=[ 0.43 0.57] 84 k=82,mus=[-0.01561079 1.87404948],sigmas=[ 1.09142987 0.90429362],priors=[ 0.43 0.57] 85 k=83,mus=[-0.01561208 1.87405037],sigmas=[ 1.09142858 0.90429286],priors=[ 0.43 0.57] 86 k=84,mus=[-0.01561315 1.8740511 ],sigmas=[ 1.09142751 0.90429223],priors=[ 0.43 0.57] 87 k=85,mus=[-0.01561403 1.8740517 ],sigmas=[ 1.09142663 0.90429172],priors=[ 0.43 0.57] 88 k=86,mus=[-0.01561476 1.8740522 ],sigmas=[ 1.0914259 0.90429129],priors=[ 0.43 0.57] 89 k=87,mus=[-0.01561537 1.87405261],sigmas=[ 1.0914253 0.90429093],priors=[ 0.43 0.57] 90 k=88,mus=[-0.01561587 1.87405295],sigmas=[ 1.0914248 0.90429064],priors=[ 0.43 0.57] 91 k=89,mus=[-0.01561629 1.87405324],sigmas=[ 1.09142438 0.90429039],priors=[ 0.43 0.57] 92 k=90,mus=[-0.01561663 1.87405347],sigmas=[ 1.09142404 0.90429019],priors=[ 0.43 0.57] 93 k=91,mus=[-0.01561692 1.87405367],sigmas=[ 1.09142376 0.90429003],priors=[ 0.43 0.57] 94 k=92,mus=[-0.01561715 1.87405383],sigmas=[ 1.09142352 0.90428989],priors=[ 0.43 0.57] 95 k=93,mus=[-0.01561735 1.87405396],sigmas=[ 1.09142333 0.90428977],priors=[ 0.43 0.57] 96 k=94,mus=[-0.01561751 1.87405407],sigmas=[ 1.09142317 0.90428968],priors=[ 0.43 0.57] 97 k=95,mus=[-0.01561764 1.87405416],sigmas=[ 1.09142303 0.9042896 ],priors=[ 0.43 0.57] 98 k=96,mus=[-0.01561775 1.87405424],sigmas=[ 1.09142292 0.90428954],priors=[ 0.43 0.57] 99 k=97,mus=[-0.01561785 1.8740543 ],sigmas=[ 1.09142283 0.90428948],priors=[ 0.43 0.57] 100 k=98,mus=[-0.01561792 1.87405435],sigmas=[ 1.09142276 0.90428944],priors=[ 0.43 0.57] 101 k=99,mus=[-0.01561799 1.8740544 ],sigmas=[ 1.09142269 0.9042894 ],priors=[ 0.43 0.57] 102 103 Process finished with exit code 0
In addition, a scikit-learn example can be found at http://scikit-learn.org/stable/modules/mixture.html
[1] Ian Goodfellow. https://www.quora.com/Why-could-generative-models-help-with-unsupervised-learning/answer/Ian-Goodfellow?srid=hTUVm
