平衡二叉树第一次是在大一下学期的数据结构上学的,记得当时自己看书上的算法描述,感觉云里雾里,各种旋转,总有种似懂非懂的样子,无奈当时的数据结构也就是那样似懂非懂地学过去了。时隔两年,转眼就大三下学期了,当我现在再次在《算法导论》上看红黑树遇到这个词的时候,不免感慨当时自己学数据结构时敲的代码实在是太少了,很多东西都没弄懂,现在才清楚地知道,要想把一个算法,一种数据结构彻底弄懂,就必须去把相应的代码落实下来,这也是给后人的一个教训呀。
闲话不多说了,在说平衡二叉树之前,我先简单地介绍一些二叉搜索树。二叉搜索树,简单来说,就是对于该树中的每个节点,如果该节点的左孩子存在,那么左孩子的关键字一定要不能大于该节点的关键字,如果该节点的右孩子存在,那么右孩子的关键字一定要不能小于该节点的关键字。这是《算法导论》上的定义。这里的关键字你可以理解为我们需要插入的那些数值,这里需要说一下的是,根据书上的定义,等于某个根节点关键字的节点既可以是它的左孩子,也可以是它的右孩子,但是这样我们处理不方便,所以实际在写程序时,我们可以规定:左孩子<根节点,右孩子>=根节点。
二叉搜索树支持的常见操作有:
1.遍历(前序,中序,后续),按照我刚才的规定,中序遍历的话输出序列是一个非递减序列,其他遍历结果就没什么意义了,所以我们只去实现它的中序遍历。
2.查找 也就是名字中的搜索,可以给定一个关键字来查找某个节点,后者查找某个节点的前驱和后继
3.插入 插入一个节点
4.删除 删除一个节点
注意,这里所有的操作的时间复杂度都是O(h),h为这棵树的高度
对于包含n个节点的二叉树,它的高度一半情况下是O(lgN),但是,也会出现某些极端情况(比如你按从小到大或者从大到小的顺序往树中插入节点),使得整棵树的形状接近一个斜的链表,这样的话树的高度就变成n,上述所有操作的时间复杂度就变成了O(N),由O(lgN)变成了O(N),这使得算法的复杂度变大了很多,而且这种情况下我们也没必要用到二叉树,毕竟它已经退化成了链表,我们何不用更简单的链表呢。
于是我们开始思考,怎么样才能让我们这棵树的高度能保持在O(lgN)的高度呢?这就是我们今天的核心问题
算法导论上讲了一种方法,就是如果我们随机构建二叉树,也就是说,对于输入的n个关键字,它们右n!种排列,我们随机选一种来作为输入序列,也就是说每个序列都是等可能出现的。那么经过严格的数学推导,我们能够证明,这棵树的高度为O(lgN)。
这种方法固然能保证它的高度为O(lgN),但是在实际应用中,显得有的苛刻。因为我们很多时候都想随心所欲地输入一组数,我们不关注这组数是怎么排列的,我们只希望按照任意一个给定的序列插入,我们都能保证树的高度是O(lgN),而不会出现O(N)的情况。那么用什么办法呢?没错,就是我今天要讲的平衡二叉树。
平衡二叉树中最重要的就是平衡二字了,那么什么叫平衡呢,要解释平衡,我们先要说一下不平衡,上面说的排成了一条链表的形状就是一种极端不平衡的表现,所以树的高度会达到最大,算法的时间复杂度也会达到最大。
平衡二叉树(AVL)的定义就是:
它或者是一颗空树,或者具有以下性质的二叉树:它的左子树和右子树的高度之差的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
显然这是一个递归定义,换句话说,对于该树中的每个节点,它的左子树的高度和右子树的高度之差都只能是-1,0,1三者中的一者。
我们规定,如果一个节点的某个子节点是空的,那么它这棵子树的高度是-1。一般而言,如果某个节点的某科子树有n层,那么它的该子树的高度是n-1。
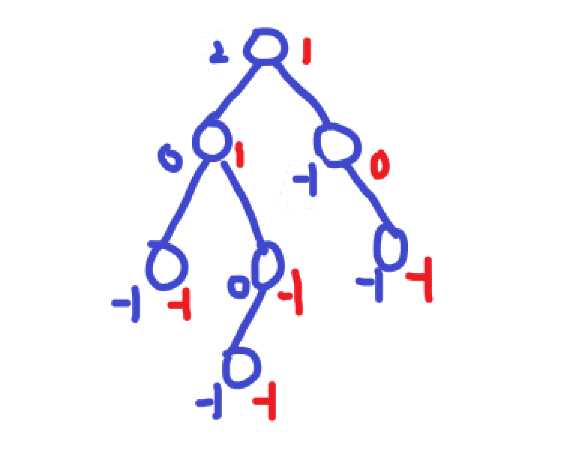
比如这种图就在每个节点旁边标出了这个节点的左子树(蓝色)和右子树(红色)的高度
像这棵树就是平衡的,因为对于它的每个节点来说,都满足我们上述要求。
而下面这棵树就不符合:
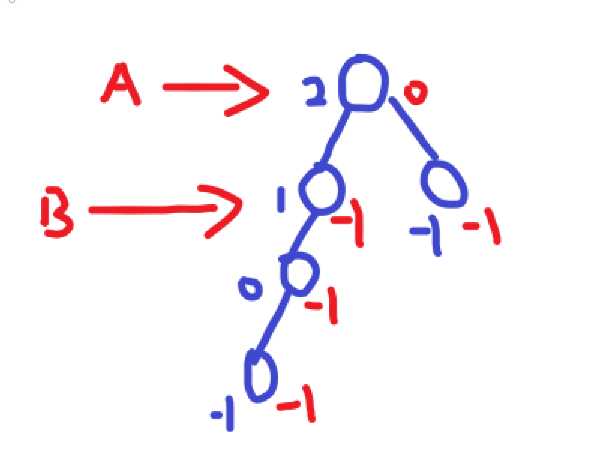
这棵树的A、B节点都不符合要求。
那么我们现在要做的就是每插入一个节点,保证插入后的整棵树的每个节点都满足上面的要求。
乍一看,好像一点头绪也没有呀,因为我们好像有无数种插入的情况,这怎么去判断当插入一个节点后,哪些节点可能违背了我们的上述要求呢?
其实,我们经过认真分析和思考,发现,其实问题没这么复杂,因为我们每插入一个节点,可能是合法的,也就是说按照我们正常的插入算法它是不会导致某个节点不平衡的,也可能是非法的,由于按照正常的插入过程,这个新插入的节点一定会变成叶节点,它的左孩子和右孩子的高度都是-1。显然,非法节点肯定不是它,那么我们要找出这样的非法节点,显然,新插入一个节点,这个节点的父节点的左子树或者右子树的高度会改变,这取决于新节点插入在父节点左孩子还是右孩子节点位置。父节点的父节点的响应子树的高度也会变化,。。。一直到整棵树的根节点的响应子树的高度都可能变化,也就是说,从整棵树的根节点到新插入的这个节点的父节点的路径上的所有属于这个 节点的祖宗节点都可能违背我们上述要求而使得我们这棵树变得不平衡。
