题目:有n条直线互相相交,其中共有p(p>=2)个交点,求能分割出的平面的个数。
一看这题,是怎样推出是一个递推式的呢?
首先考虑每一条直线,他们相交共有两种情况:一种是全都相交于一点,另一种是不相交于一点。
那好,先来分析相交于一点的情况:
一条直线把平面分割成两个。
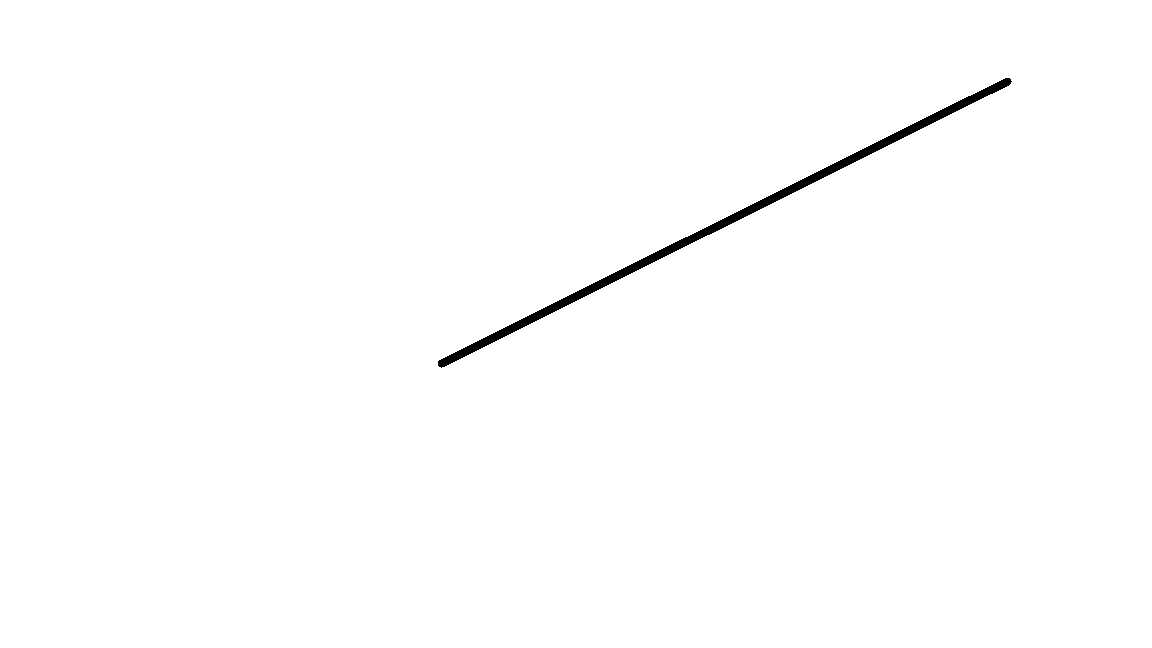
两条直线把平面分割成四个。
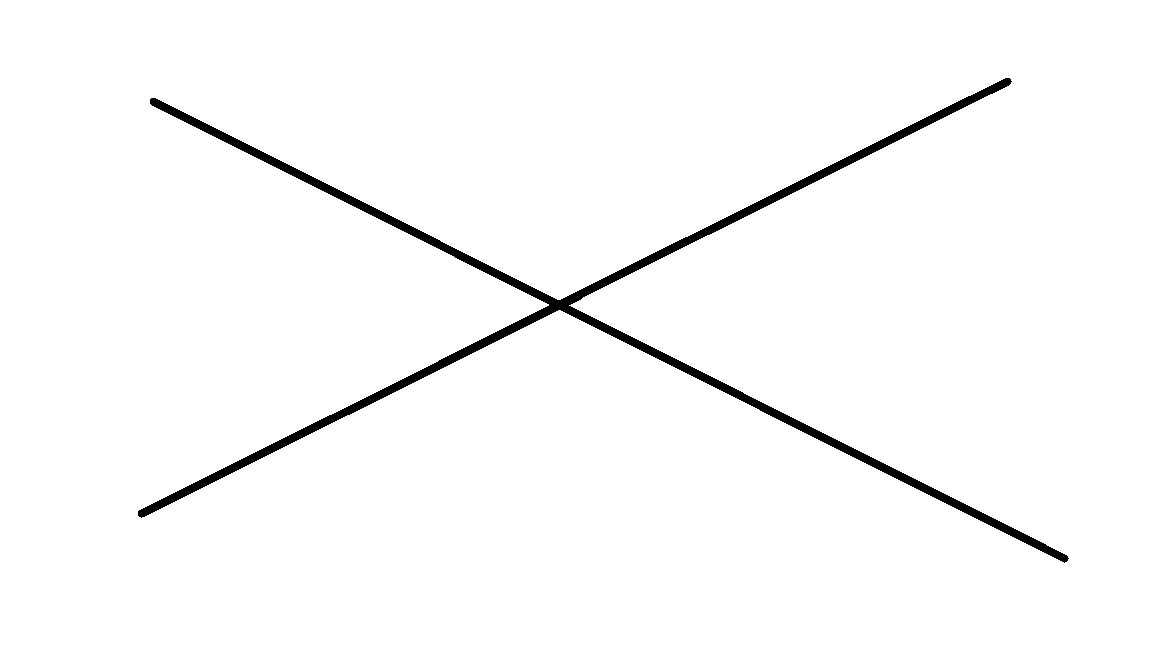
三条直线把平面分成六个;
四条直线把平面分成八个
……
n条直线把平面分成2*n个。
这样若干条直线相交于一点的情况就能推出来一个式子了。
接着再来考虑另一种情况,就是他们不是相交于一点的:
我们不妨也来以每一条直线为基本单位来推,假设p=3,那么从第四条直线开始思考:

第四条直线在原来的六个平面上又加了四个平面,2*3+4=10
再假设p=4,从第五条直线开始思考:
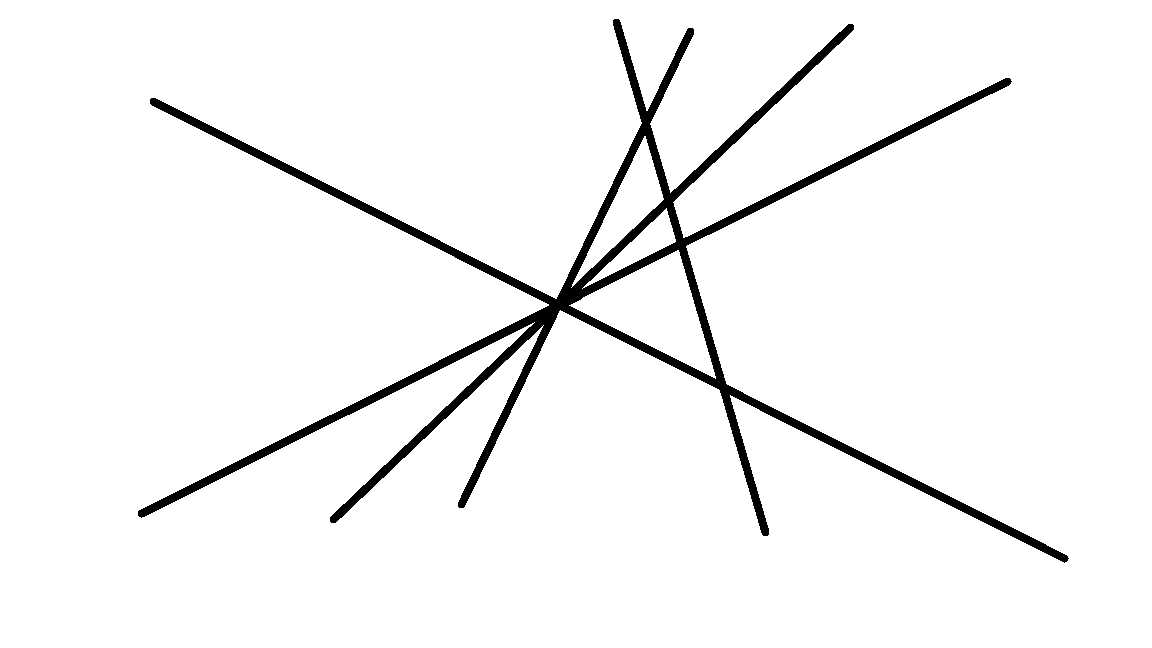
第五条在原来的八个平面上加了五个平面 2*4+5=13
所以能找出规律:p+1条直线添加了p+1个平面,要考虑一般情况,还得再考虑p+2,p+3……p+n这些直线。
还是上面的p=4的图,当添加第六条直线时:
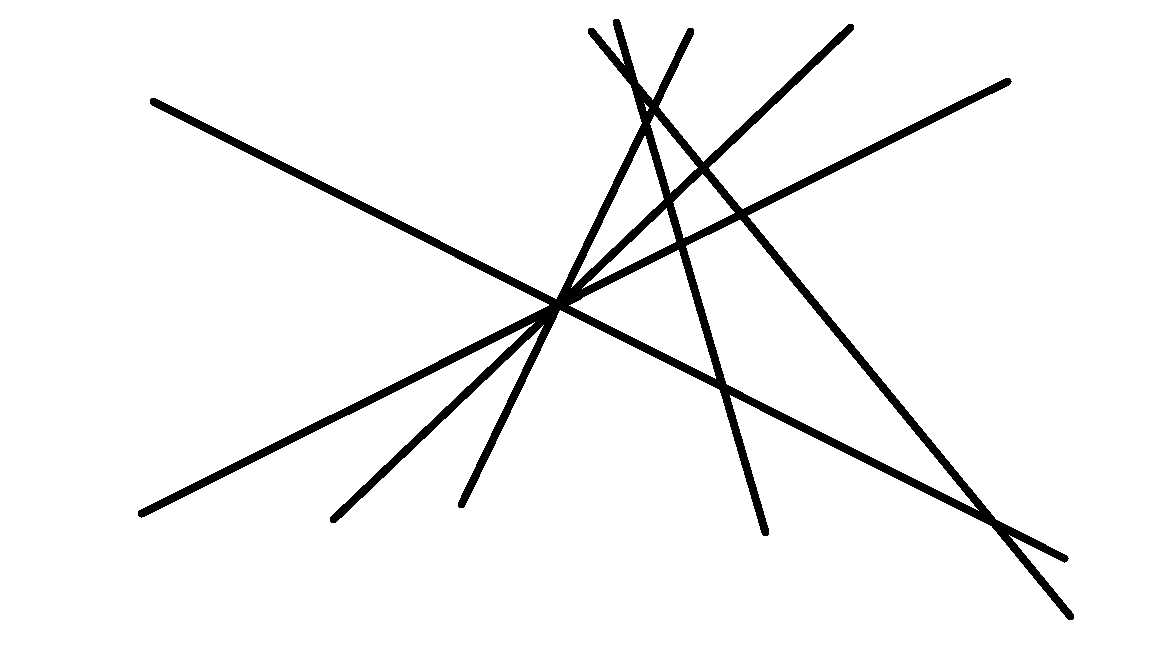
平面的个数又加了六个,则可以推出第七条加了七个,第n条加了n个。
所以综合以上几种情况,可以得出递推式为2*p+(n+p+1)*(n-p)/2,这一个式子就可以把所有式子全部包含了,代码:
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; int n,p; int main() { scanf("%d%d",&n,&p); printf("%d",2*p+(n+p+1)*(n-p)/2); return 0; }
这是一道运用分类讨论思想的递推题,只要把每种情况的式子列好,那么整合两种情况就可以解决。
