Lecture 1: Complexity Analysis
How to measure Running time: Use a function to model the running time of a program or procedure.
- Assume an abstract machine and count the number of “steps” executed by an algorithm
Function: In mathematics, a function is a relation between a set of inputs and a set of allowed outputs with the property that each input is related to exactly one output
How to Model Running Time as a function:
Compare the functions of Running Time models:
Consider the order of growth of running time, not the actual value
The order of growth rate
- Give a simple characterization of the algorithm’s efficiency
- Allow us to compare the relative performance of alternative algorithms
In the analysis of algorithms, we need to consider the performance of algorithms when applied to very very big input datasets, e.g., very large n (i.e., asymptotic analysis)
TA(n) = 100n + 50
TB(n) = (0.5)n2 + 4.5n + 5
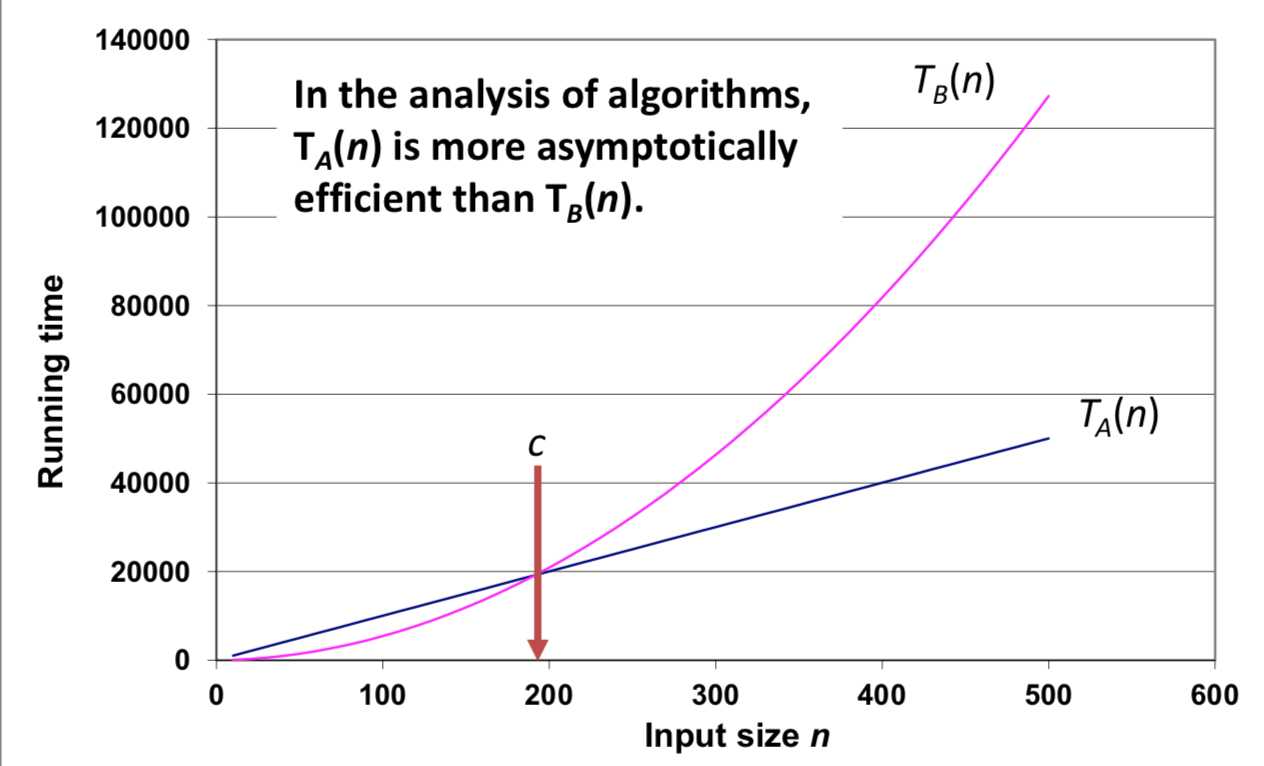TA(n) > TB(n) if n < c, but TA(n) < TB(n) if n > c
Asymptotic Notation - notations to express the growth rate of a function (Just for function)
A way to compare ‘size‘ of functions:
– ο-notation (“Big-oh”) ≈≤ (upper bound)
– Ω-notation (“Big-omega”) ≈≥ (lower bound)
– θ-notation (“theta”) ≈= (in between)
