题目
在社交网络(socialnetwork)的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。
在一个社交圈子里有n个人,人与人之间有不同程度的关系。我们将这个关系网络对应到一个n个结点的无向图上,
两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值c,c越小,表示两个人
之间的关系越密切。我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度,注意到最短路
径上的其他结点为s和t的联系提供了某种便利,即这些结点对于s和t之间的联系有一定的重要程度。我们可以通过
统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。考虑到两个结点A和B之间可能会有
多条最短路径。我们修改重要程度的定义如下:令Cs,t表示从s到t的不同的最短路的数目,Cs,t(v)表示经过v从s
到t的最短路的数目;则定义
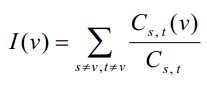
为结点v在社交网络中的重要程度。为了使I(v)和Cs,t(v)有意义,我们规定需要处理的社交网络都是连通的无向图
,即任意两个结点之间都有一条有限长度的最短路径。现在给出这样一幅描述社交网络的加权无向图,请你求出每
一个结点的重要程度。
输入格式
输入第一行有两个整数n和m,表示社交网络中结点和无向边的数目。在无向图中,我们将所有结点从1到n进行编号
。接下来m行,每行用三个整数a,b,c描述一条连接结点a和b,权值为c的无向边。注意任意两个结点之间最多有
一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。n≤100;m≤4500
,任意一条边的权值 c 是正整数,满足:1≤c≤1000。所有数据中保证给出的无向图连通,且任意两个结点之间
的最短路径数目不超过 10^10
输出格式
输出包括n行,每行一个实数,精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。
输入样例
4 4
1 2 1
2 3 1
3 4 1
4 1 1
输出样例
1.000
1.000
1.000
1.000
提示
社交网络如下图所示。
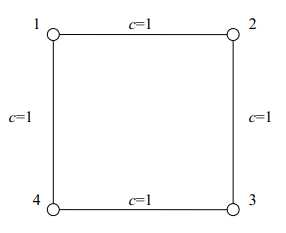
对于 1 号结点而言,只有 2 号到 4 号结点和 4 号到 2 号结点的最短路经过 1 号结点,而 2 号结点和 4 号结
点之间的最短路又有 2 条。因而根据定义,1 号结点的重要程度计算为 1/2 + 1/2 = 1 。由于图的对称性,其他
三个结点的重要程度也都是 1 。
题解
n很小,立刻想到floyd
跑一遍可以求出最短路及路径数
跑第二次可以更新中介点的答案
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<‘ ‘; puts("");
using namespace std;
const int maxn = 105,maxm = 100005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57) {if (c == ‘-‘) flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - ‘0‘; c = getchar();}
return out * flag;
}
double d[maxn][maxn],cnt[maxn][maxn],f[maxn];
int n,m;
void floyd(){
REP(k,n) REP(i,n) REP(j,n){
if (i == k || i == j || k == j) continue;
if (d[i][k] + d[j][k] < d[i][j])
d[i][j] = d[i][k] + d[k][j],cnt[i][j] = cnt[i][k] * cnt[k][j];
else if (d[i][k] + d[k][j] == d[i][j])
cnt[i][j] += cnt[i][k] * cnt[k][j];
}
REP(k,n) REP(i,n) REP(j,n){
if (i == k || i == j || k == j) continue;
if (d[i][k] + d[k][j] == d[i][j])
f[k] += cnt[i][k] * cnt[k][j] / cnt[i][j];
}
}
int main(){
n = read(); m = read(); int a,b,v;
fill(d[0],d[0] + maxn * maxn,INF);
REP(i,n) d[i][i] = 0;
while (m--){
a = read(); b = read(); v = read();
d[a][b] = d[b][a] = v; cnt[a][b] = cnt[b][a] = 1;
}
floyd();
REP(i,n) printf("%.3lf\n",f[i]);
return 0;
}