日常留坑。。。。
本文只讨论FFT在信息学奥赛中的应用
文中内容均为个人理解,如有错误请指出,不胜感激
前言
先解释几个比较容易混淆的缩写吧
DFT:离散傅里叶变换—>$O(n^2)$计算多项式乘法
FFT:快速傅里叶变换—>$O(n*\log(n)$计算多项式乘法
FNTT/NTT:快速傅里叶变换的优化版—>优化常数及误差
FWT:快速沃尔什变换—>利用类似FFT的东西解决一类卷积问题
多项式
系数表示法
设$A(x)$表示一个$n-1$次多项式
则$A(x)=\sum_{i=0}^{n} a_i * x^i$
例如:$A(3)=2+3*x+x^2$
利用这种方法计算多项式乘法复杂度为$O(n^2)$
(第一个多项式中每个系数都需要与第二个多项式的每个系数相乘)
点值表示法
将$n$互不相同的$x$带入多项式,会得到$n$个不同的取值$y$
则该多项式被这$n$个点$(x_1,y_1),(x_2,y_2),\dots,(x_n,y_n)$唯一确定
其中$y_i=\sum_{j=0}^{n-1} a_j*x_i^j$
例如:上面的例子用点值表示法可以为$(0,2),(1,5),(2,12)$
利用这种方法计算多项式乘法的时间复杂度仍然为$O(n^2)$
(选点$O(n)$,每次计算$O(n)$)
我们可以看到,两种方法的时间复杂度都为$O(n^2)$,我们考虑对其进行优化
对于第一种方法,由于每个点的系数都是固定的,想要优化比较困难
对于第二种方法,貌似也没有什么好的优化方法,不过当你看完下面的知识,或许就不这么想了
复数
在介绍复数之前,首先介绍一些可能会用到的东西
向量
同时具有大小和方向的量
在几何中通常用带有箭头的线段表示
圆的弧度制
等于半径长的圆弧所对的圆心角叫做1弧度的角,用符号rad表示,读作弧度。用弧度作单位来度量角的制度叫做弧度制
公式:
$1^{\circ }=\dfrac{\pi}{180}rad$
$180^{\circ }=\pi rad$
平行四边形定则
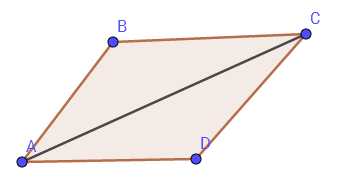
(好像画的不是很标准。。)
平行四边形定则:AB+AD=AC
复数
定义
设$a,b$为实数,$i^2=-1$,形如$a+bi$的数叫负数,其中$i$被称为虚数单位,复数域是目前已知最大的域
在复平面中,$x$代表实数,$y$轴(除原点外的点)代表虚数,从原点$(0,0)$到$(a,b)$的向量表示复数$a+bi$
模长:从原点$(0,0)$到点$(a,b)$的距离,即$\sqrt{a^2+b^2}$
幅角:假设以逆时针为正方向,从$x$轴正半轴到已知向量的转角的有向角叫做幅角
运算法则
加法:
因为在复平面中,复数可以被表示为向量,因此复数的加法与向量的加法相同,都满足平行四边形定则(就是上面那个)
乘法:
几何定义:复数相乘,模长相乘,幅角相加
代数定义:$$(a+bi)*(c+di)$$
$$=ac+adi+bci+bdi^2$$
$$=ac+adi+bci-bd$$
$$=(ac-bd)+(bc+ad)i$$
单位根
下文中,默认$n$为$2$的正整数次幂
在复平面上,以原点为圆心,$1$为半径作圆,所得的圆叫做单位圆。以原点为起点,单位圆的$n$等分点为终点,作$n$个向量。设所得的幅角为正且最小的向量对应的复数为$\omega _{n}$,称其为$n$次单位根
例如
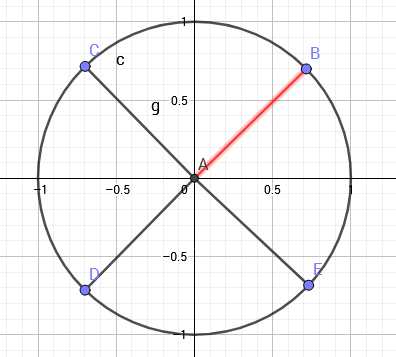
图中向量$AB$表示的复数为$4$次单位根
单位根的幅角为周角的$\dfrac{1}{n}$
在代数中,若$z^n=1$,我们把$z$称为$n$次单位根
单位根的性质
- $\omega _{n}^{k}=cosk\dfrac{n}{2\pi}$
- $\omega _{2n}^{2k}=\omega _{n}^{k}$
证明:将等式左边根据展开后即可得到右边
- $\omega _{n}^{k+\dfrac{n}{2}}=-\omega _{n}^{k}$
证明:将$\omega _{n}^{\dfrac{n}{2}}$展开,发现其值等于$-1$
- $\omega _{n}^{0}=\omega _{n}^{n}=1$
n??,称为 n n n 次单位根。
n??,称为 n n n 次单位根。
