二叉树一共有4种遍历: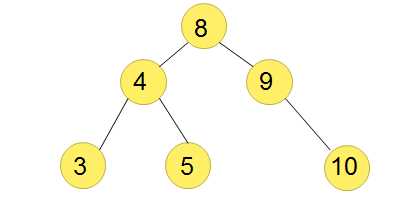
1.层次遍历(8-4-9-3-5-10)
2.前序遍历(8-4-3-5-9-10)
3.中序遍历(3-4-5-8-9-10)
4.后序遍历(3-5-4-10-9-8)
其中后三种遍历又分别分为递归遍历与非递归遍历,我们重点说非递归遍历。
非递归前序遍历
思路:判断节点非空------打印-----入栈------向左走
1 void PreOrder(BinaryTree*p) 2 { 3 stack<BinaryTree*>st; 4 while(p||!st.empty()) 5 { 6 if(p!=NULL) 7 { 8 cout<<p->value<<endl; 9 st.push(p); 10 p=p->left; 11 } 12 else 13 { 14 p=st.top(); 15 st.pop(); 16 p=p->right; 17 } 18 } 19 }
非递归中序遍历
思路:与前序不同的就是打印是在出栈前打印的
void InOrder(BinaryTree*p) { stack<BinaryTree*>st; while(p||!st.empty()) { if(p!=NULL) { st.push(p); p=p->left; } else { p=st.top(); cout<<p->value<<endl; st.pop(); p=p->right; } } }
非递归后序遍历
后序遍历递归定义:先左子树,后右子树,再根节点。后序遍历的难点在于:需要判断上次访问的节点是位于左子树,还是右子树。若是位于左子树,则需跳过根节点,先进入右子树,再回头访问根节点;若是位于右子树,则直接访问根节点。
思路:添加一个标记(pmark),具体解释见代码中。
1 void LastOrder(BinaryTree *p) 2 { 3 stack<BinaryTree*>st; 4 BinaryTree *pmark=NULL; 5 while(p||!st.empty()) 6 { 7 if(p!=NULL){ 8 st.push(p); 9 p=p->left; 10 }//走到最左 11 else 12 { 13 if(st.top()->right==pmark||st.top()->right==NULL) 14 { 15 pmark=st.top();//第一次进来的时候将最右节点10赋给pmark,第二次进入if是因为满足右节点10被处理过(此时栈顶元素为9,右孩子为10,此时pmark指向的就是10) 16 st.pop(); 17 printf("%d\n",pmark->value); 18 } 19 else 20 p=st.top()->right;//一直走,走到最右,第一次进入if中(满足st.top()->right==NULL) 21 22 } 23 24 } 25 }
递归前序遍历
1 void preorder(BinaryTree* t) 2 { 3 if(t==NULL) return ; 4 printf("%d\n",t->value); 5 preorder(t->left); 6 preorder(t->right); 7 }
递归中序遍历
1 void inorder(BinaryTree* t) 2 { 3 if(t==NULL) return ; 4 inorder(t->left); 5 printf("%d\n",t->value); 6 inorder(t->right); 7 }
