本篇博客中题目的代码均位于文末,文中不再出现
算法原理
对于快速傅里叶变换的原理,可以参考上面的博客以及《算法导论》
大体说明
FFT用于加速多项式的乘法:
\[H(x)=f(x) \otimes g(x)\]
即:
\[H(t)=\sum^{t}_{k=0}f(k)*g(t-k)\]
上面两个式子都是卷积的形式,也就是FFT可以优化的类型
使用暴力做法,时间复杂度为 \(O(n^2)\),而使用快速傅里叶变换可以做到\(O(nlogn)\),于是许多问题从不可做变成了可做,FFT对生成函数的优化是个很好的例子,可以快速解决组合问题。
题目
模板
或者bzoj2179
FFT优化高精度乘法,一个数就可以看作\(f(10)\),其中:
\[f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots\]
BZOJ2194: 快速傅立叶之二
Description
请计算\(C_k=\sum_{i=k}^{n-1}A_i*B_{i-k}\)其中 \(k \leq i < n\) ,并且有 \(n \leq 10 ^ 5\) 。\(A\) , \(B\) 中的元素均为小于等于100的非负整数。\(A\) , \(B\)最高次项均为 \(n-1\)
Solution
没错,就是一个多项式的乘法
我们将上面那个式子变一下形
首先将 \(A\) 的系数全部 reverse
eg:
\[A(x)=a_0+a_1x+a_2x^2+a_3x^3\]
\[A^R(x)=a_3+a_2x+a_1x^2+a_0x^3\]
此时
\[C_k=\sum_{i=k}^{n-1}A^R_{n-i-1}*B_{i-k}\]
然后改变求和指标,上式变为
\[C_k=\sum_{i=0}^{n-k-1}A^R_{n-i-k-1}*B_{i}\]
另 \(t=n-k-1\),则 \(k=n-t-1\),代入上式可得
\[C_{n-t-1}=\sum_{i=0}^{t}A^R_{t-i}*B_{i}\]
与之前类似地:
\[C^R_{t}=\sum_{i=0}^{t}A^R_{t-i}*B_{i}\]
因此我们只需要将 \(A\) 反转,得到的卷积结果是 \(C\) 的反转
BZOJ3527: [Zjoi2014]力
Description
给出 \(n\) 个数 \(q_i\),给出 \(F_j\) 的定义如下:
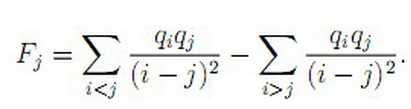
令 \(E_i=F_i/q_i\) ,求 \(E_i\).
\(n≤100000,0<qi<1000000000\)
Solution
很显然,\[E_k=\sum_{i<k}\frac{q_i}{(i-k)^2}-\sum_{i>k}\frac{q_i}{(i-k)^2}\]
另 \(f(x)=q_x\),$ g(x)=\frac{1}{i^2}$,那么:
\[\sum^{k-1}_{i=0}\frac{q_i}{(i-k)^2}=f(x) \otimes g(x)\]
而另一部分与BZOJ2194类似:
\[reverse(\sum_{i>k}\frac{q_i}{(i-k)^2})=f(x) \otimes g^R(x)\]
两次答案加起来就是最终答案
另:这题卡精度,计算 \(g(x)\) 时要 \(g(i)=1/i/i\),不能\(g(i)=1/(i*i)\)
BZOJ3771: Triple
Description
我们讲一个悲伤的故事。
从前有一个贫穷的樵夫在河边砍柴。
这时候河里出现了一个水神,夺过了他的斧头,说:
“这把斧头,是不是你的?”
樵夫一看:“是啊是啊!”
水神把斧头扔在一边,又拿起一个东西问:
“这把斧头,是不是你的?”
樵夫看不清楚,但又怕真的是自己的斧头,只好又答:“是啊是啊!”
水神又把手上的东西扔在一边,拿起第三个东西问:
“这把斧头,是不是你的?”
樵夫还是看不清楚,但是他觉得再这样下去他就没法砍柴了。
于是他又一次答:“是啊是啊!真的是!”
水神看着他,哈哈大笑道:
“你看看你现在的样子,真是丑陋!”
之后就消失了。
樵夫觉得很坑爹,他今天不仅没有砍到柴,还丢了一把斧头给那个水神。
于是他准备回家换一把斧头。
回家之后他才发现真正坑爹的事情才刚开始。
水神拿着的的确是他的斧头。
但是不一定是他拿出去的那把,还有可能是水神不知道怎么偷偷从他家里拿走的。
换句话说,水神可能拿走了他的一把,两把或者三把斧头。
樵夫觉得今天真是倒霉透了,但不管怎么样日子还得过。
他想统计他的损失。
樵夫的每一把斧头都有一个价值,不同斧头的价值不同。总损失就是丢掉的斧头价值和。
他想对于每个可能的总损失,计算有几种可能的方案。
注意:如果水神拿走了两把斧头 \(a\) 和 \(b\) ,\((a,b)\) 和 \((b,a)\) 视为一种方案。拿走三把斧头时,\((a,b,c),(b,c,a),(c,a,b),(c,b,a),(b,a,c),(a,c,b)\) 视为一种方案。
Description2
嗯,一句话,有 \(n\) 个物品各有价值,要求从中取出 \(1\) 到 \(3\) 个物品,不同排列视作同一种,求可能的取出物品的价值和有多少种
所有数据满足: \(Ai \leq 40000\)
Solution
我们直接构造出这些斧头的生成函数
举个例子,有斧子们 \(2,4,4,4,6,8,8,9\)
则其对应的生成函数为
\[f(x)=x^2+3x^4+x^6+2x^8+x^9\]
在这一题里,我们记取一把斧子的生成函数为 \(F(x)\),取两把相同的斧子的生成函数为 \(G(x)\) , 三把为 \(H(x)\) 那么取一个斧头的方案就是 \(F(x)\);
对于两个斧头,方案数变为了\((F(x)\otimes F(x)-G(x))/2\)
对于三把斧头,方案数就是 \((F(x)\otimes F(x)\otimes F(x) - 2\times G(x)*F(x) - H(x))/6\)
上边的计算,只要理解生成函数再使用容斥原理就可以了
注:对于函数的操作,可以直接转化为点值表达后一起搞事,不用每次 \(DFT\)、\(IDFT\),可以参见代码
BZOJ3509: [CodeChef] COUNTARI
Description
给定一个长度为 \(N\) 的数组 \(A[\ ]\) ,求有多少对 \(i,j,k\) \((1\leq i<j<k\leq N)\)满足 \(A[k]-A[j]=A[j]-A[i]\) 。
\(N\leq 100000 ,A[i]\leq 30000\)
Solution
首先,通过移项,不难发现,我们要求的是对于每一个 \(j\) 满足 \(2A[j]=A[i]+A[k]\) 的 \(i,k\) 对数 \((1\leq i<j<k\leq N)\)
所以我们直接从头到尾扫一遍,分别维护前缀及后缀里各个值出现的次数,看对于当前 \(j\) 有那些组合满足条件。时间复杂度 \(O(n^3)\)
此时我们再来看这个式子\(2A[j]=A[i]+A[k]\),这个也是可以使用生成函数的。
先把前缀及后缀的生成函数搞出来,分别记为 \(f(x),g(x)\)。
令 \(h(x)=f(x)\otimes g(x)\),那么,函数 \(h(x)\) 的第 \(x^{2j}\) 项的系数就是对于当前 \(j\) 满足条件的对数,卷积可以用FFT优化到 \(O(nlogn)\) 。
可惜的是这玩意最终的时间复杂度是 \(O(n^2logn)\),硬上并无卵用
用了FFT还是这么慢的主要原因是用了太多次,可不可以用少一些呢?
现在我们将待处理的数列分为 \(\sqrt{nlogn}\)个块,对于块内,暴力解决,而对于块外则使用FFT。
具体来说就是在一个块 \([L,R]\) 中,可以通过暴力统计计算出满足 \(1 \leq i < L \leq j < k \leq R\) 以及 \(L \leq i < j \leq R < k \leq N\)的方案数;
而对于\(1 \leq i < L \leq j \leq R < k \leq N\),我们构造 \([1,L)\) 的生成函数以及 \((R,N]\) 的生成函数,卷积一下就是方案数了;
最终两个答案加一起就是最终答案
另:这题要注意常数
BZOJ3456: 城市规划
Description
刚刚解决完电力网络的问题, 阿狸又被领导的任务给难住了.
刚才说过, 阿狸的国家有 \(n\) 个城市,现在国家需要在某些城市对之间建立一些贸易路线,使得整个国家的任意两个城市都直接或间接的连通.为了省钱,每两个城市之间最多只能有一条直接的贸易路径.对于两个建立路线的方案, 如果存在一个城市对, 在两个方案中是否建立路线不一样, 那么这两个方案就是不同的, 否则就是相同的. 现在你需要求出一共有多少不同的方案.好了, 这就是困扰阿狸的问题. 换句话说, 你需要求出 \(n\) 个点的简单(无重边无自环)无向连通图数目.由于这个数字可能非常大,你只需要输出方案数 \(mod ~ 1004535809(479 * 2 ^ 21 + 1)\) 即可.
Solution
首先对于这个模数,已经暴露了题目想让我们搞什么——快速数论变换
下文直接用 \(\binom{n}{i}\) 表示 \(C_n^i\)
我们记最终的答案为一个函数 \(f(x)\),那么 \(f(n)\) 是最终答案。
如果不考虑这个图的连通性,那么答案就显然是 \(\large 2^{\binom{n}{2}}\),即所有可能的边选或者不选。设 \(\large g(x)=2^{\binom{x}{2}}\)
进一步考虑,如何找出 \(g\) 与 \(f\) 的等量关系?
我们枚举 \(1\) 号点所在的连通块,我们可以得到以下的等量关系:
\[g(n)=\sum_{i=1}^{n}\binom{n-1}{i-1}f(i)g(n-i)\]
同时除以 \((n-1)!\) 得
\[\frac{g(n)}{(n-1)!}=\sum_{i=1}^{n}\frac{f(i)}{(i-1)!}\frac{g(n-i)}{(n-i)!}\]
是不是看到了卷积?美滋滋
令:(这样写好像不规范)
\[H(x)=\frac{g(x)}{(x-1)!},F(x)=\frac{f(x)}{(x-1)!},G(x)=\frac{g(x)}{(x)!}\]
其中为了求逆元 \(G(0)=1\)
\[\because H(x)=F(x)\otimes G(x)\]
\[\therefore F(x)=H(x)\otimes G^{-1}(x) \]
只要求一个 \(G(x)\) 逆元一卷积就好了(求逆元的方法回头再说)
BZOJ4503: 两个串
Description
兔子们在玩两个串的游戏。给定两个字符串 \(S\) 和 \(T\) ,兔子们想知道 \(T\) 在 \(S\) 中出现了几次,
分别在哪些位置出现。注意T中可能有 \(“?”\) 字符,这个字符可以匹配任何字符。
\(S\) 长度不超过 \(10^5\), \(T\) 长度不会超过 \(S\)。 \(S\) 中只包含小写字母,T中只包含小写字母和 \(“?”\)
Solution
如果两个长度为 \(len\) 的串 \(s1,s2\) 相等时,我们可以写成
\[\sum_{i=0}^{len-1}\left| s1[i]-s2[i] \right|=0\]
也可以写成
\[\sum_{i=0}^{len-1}(s1[i]-s2[i])^2=0\]
现在将 \(s2\) 翻转,得到 \(s3\),上式就可以写成
\[\sum_{i=0}^{len-1}(s1[i]-s3[(len-1)-i])^2=0\]
我们记 \(S,T\) 中所对应的各字符减去 \(‘a‘\) 的值记为 \(f,g\),其中当字符为 \(?\) 时,将这个值赋为 \(0\),就可以有一下关系(\(g\) 的系数颠倒后为 \(g^R\))
\[Ans=(f-g^R)^2\otimes g^R\]
感觉不用解释了, \(Ans\) 的某一位是 \(0\) 的时候就意味着有一个满足题意的匹配
BZOJ3160: 万径人踪灭
Description



Solution
并没有看完整题意。。。
首先,如果回文串要求连续的,可以通过 \(Manacher\) 算法 \(O(n)\) 内很轻松解决
这个Manacher讲的不错
那此时就可以计算所有的,不管连续不连续的回文串,再减去连续的就行了
对于计算回文串个数,可以通过一下式子
\[Ans_t=\sum_{i=0}^{t}s1[i]\times s2[i]\]
解释一下,由于只有 \(a,b\) 两种字符,我们把数列中的 \(a\) 赋为 \(1\) , \(b\) 赋为 \(0\),做一次计算;
再把数列中的 \(b\) 赋为 \(1\) , \(a\) 赋为 \(0\),做一次计算;两次结果相加。
这样可以得到以 \(\frac{t}{2}\) 为中心的、最长的、不管连续不连续的回文串。
那么其数量为 \(2^{Ans_t}\)。
最后把所有答案加起来减去连续的回文串数量就行
BZOJ3992: [SDOI2015]序列统计
Description
小C有一个集合 \(S\),里面的元素都是小于 \(M\) 的非负整数。他用程序编写了一个数列生成器,可以生成一个长度为N的数列,数列中的每个数都属于集合 \(S\) 。
小C用这个生成器生成了许多这样的数列。但是小C有一个问题需要你的帮助:给定整数 \(x\) ,求所有可以生成出的,且满足数列中所有数的乘积\(mod\ M\)的值等于 \(x\) 的不同的数列的有多少个。小C认为,两个数列\(\{A_i\}\)和\(\{B_i\}\)不同,当且仅当至少存在一个整数 \(i\) ,满足 \(A_i\neq B_i\)。另外,小C认为这个问题的答案可能很大,因此他只需要你帮助他求出答案\(mod\ 1004535809\)的值就可以了。
输入:一行,四个整数,N、M、x、|S|,其中|S|为集合S中元素个数。第二行,|S|个整数,表示集合S中的所有元素。
对于10%的数据,1<=N<=1000;
对于30%的数据,3<=M<=100;
对于60%的数据,3<=M<=800;
对于全部的数据,1<=N<=109,3<=M<=8000,M为质数,1<=x<=M-1,输入数据保证集合S中元素不重复
Solution
模数又暴露了算法,但并不影响这是个神题
首先 \(M\) 是个质数,我们可以找到其原根
原根是什么?
假设一个数 \(g\) 对于 \(P\) 来说是原根,那么 \(g^i\ mod\ P\)的结果两两不同,且有 \(1<g<P, 1<i<P\),那么 \(g\) 可以称为是 \(P\) 的一个原根
简单来说,\(g^i\ mod\ p \neq g^j\ mod\ P\) ( \(P\) 为素数)
关于其计算,参见这里
简而言之,每次枚举原根,暴力看是否满足条件
//qpow(x,k,MOD)为快速幂 : x^k %MOD
bool judge(int val){
if(m==2)
return 1;
if(val==1)
return 0;
for(int i=2;i*i<=m;i++)
if((m-1)%i==0)
if(qpow(val,m/i,m)==1)
return 0;
return 1;
}
int FindG(int val){
int re=1;
while(!judge(re)) re++;
return re;
}另 \(M\) 的原根是 \(g\)
这时,每个数 \(a_i\) 就可以写成 \(\large g^{b_i}=a_i\)
所以
\[\prod a_i\]
就变成了
\[\large g^{\sum b_i}\]
这一步将乘法运算变为了加法
现在将 \(b\) 构造生成函数记为 \(B\)
显然,因为每个数可以取多次
\[Ans=B^n\]
\(Ans\) 的第 \(X\) 位就是最终答案
时间复杂度 \(O(mlogmlogn)\)
注:
1.多项式快速幂的时候不能把次数高于 \(M\) 的项直接清零,而是应该将第 \(k\) 项加到 \(k\ mod\ (m-1)\) 项上
2.对于 \(X=0\) 特别计算
BZOJ3557: [Ctsc2014]随机数
Description
露露、花花和萱萱最近对计算机中的随机数产生了兴趣。为大家所熟知的是,有计算机生成的随机数序列并非真正的随机数,而是由一定法则生成的伪随机数。 某一天,露露了解了一种生成随机数的方法,成为Mersenne twister。给定初始参数 \(m∈Z^+,x∈Z^+∩[0,2m)\)和初值 \(M0∈Z^+∩[0,2m)\),它通过下列递推式构造伪随机数列\({M_n}\):

其中XOR是二进制异或运算(C/C++中的^运算)。而参数x的选取若使得该数列在长度趋于无穷时,近似等概率地在 \(Z^+\bigcap(0,2m)\) 中取值,
就称x为好的。例如,在 \(m>1\) 时 \(x=0\) 就显然不是好的。
在露露向伙伴们介绍了Mersenne twister之后,花花想用这一些经典的随机性测试来检验它的随机性强度。为此,花花使用计算机计算
了一些 \(M_k\)。
但细心的萱萱注意到,花花在某次使用二进制输入 \(k\) 时,在末尾多输入了 \(l\) 个 \(0\) 。她正想告诉花花这个疏忽,然而花花已经计算并记录了错误的 \(M_k\) 而没有记录 \(k\) 的值。虽然这其实不是什么致命的问题,但是在萱萱告诉花花她这个疏漏时,作为完美主义者的花花还是恳求萱萱帮她修正 \(M_k\) 的值。萱萱便把这个任务交给了她的AI——你。
Input:
第一行包含一个正整数 \(m\) ,
第二行为二进制表示的 \(x\)(共 \(m\) 个数,从低位到高位排列)
第三行为二进制表示的 \(M_0\)(排列方式同 \(x\) ),
第四行包含一个整数 \(type\)。
接下来分为两种可能的情况:
- \(type=0\) (萱萱记下了花花的输入):则第五行包含一个整数,表示萱萱记下来的正确的k值。
2.\(type=1\) (萱萱未能记下花花的输入):则第五行为 \(l\) ,第六行输入花花计算出错误的二进制表示的 \(M_k\)。
Output:
仅一行,为 \(m\) 位的 \(01\) 串,表示你求得的正确 \(M_k\)(同样要求从低位到高位)。
\(M\leq1000000, K\leq10^6\)
Solution
我们可以直接将 \(x,M0\) 看做两个 \(GF(2)\) (系数mod2)下的多项式 \(M_0(x),X(x)\)
在此意义下(\(\oplus\) 为异或)
\[A(x) \oplus B(x) \Leftrightarrow A(x)\pm B(x)\]
所以上面两个操作看成
\[M_n=xM_{n-1}\]
以及
\[M_n=(xM_{n-1}-x^{m})\oplus X(x)\]
这样两种操作都可以写成
\[M_n=xM_{n-1}\ mod\ (x^m+X(x))\]
仔细分析上式是对的
1.操作一由于最高次项不到 \(m\) 取模是没有影响的
2.操作二就是这么个东西
于是 \(type=0\),可以直接计算出
\[M_k(x)=x^kM_0(x)\ mod\ (x^m+X(x))\]
需要多项式快速幂以及多项式取模(和除法在一起)
对于 \(type=1\)
因为题目保证 \(x\) 是“好的”,每次操作都是确定的,可以发现一个性质,\(M_k\) 在 \([0,2^m)\)里恰好每个值出现过一遍,否则 \(x\) 不可能是好的,最后不是等概率。
将上面这个性质写成式子就是\(x\equiv x^{2^m}\ mod\ (x^m+X(x))\)
我们再将问题表示出来
\[x^{k2^l}M_0(x)\equiv M_{k2^l}(x)\ mod\ (x^m+X(x))\]
再利用上面的性质整理
\[x^{k2^l2^{m-l}}\equiv (M_{k2^l}(x)M_0^{-1}(x))^{2^{m-l}}\ mod\ (x^m+X(x))\]
所以
\[x^k\equiv (M_{k2^l}(x)M_0^{-1}(x))^{2^{m-l}}\ mod\ (x^m+X(x))\]
所以
\[M_k(x)\equiv x^kM_0(x)\equiv (M_{k2^l}(x)M_0^{-1}(x))^{2^{m-l}}M_0(x)\ mod\ (x^m+X(x))\]
所以只要求出 \(M_0(x)\) 在 \(\ mod\ (x^m+X(x))\) 下的逆元,与 \(M_{k2^l}(x)\) 乘起来计算快速幂,再乘上 \(M_0\) 就行了
求出 \(M_0(x)\) 在 \(\ mod\ (x^m+X(x))\) 下的逆元需要拓展欧几里得,这与数论里的方法类似
吐槽一下:
1.这题真是个板子大全(没有开根)
2.真不可调试//用了一整个上午,还是有标程的情况下,代码里的DEBUG()可以看出我的绝望
3.原题一个点时限20sec,搞到测试数据一测最大点15sec,然而BZOJ丧心病狂总时间160sec(20个点),我现在已经没心情去卡常了,就这了(这意味着我的代码会TLE,但是肯定对)
4.%%%WJMZBMR,%%%miskcoo
Code
BZOJ3557
/**************************************************************
Problem: 3557
User: zzzc18
Language: C++
Result: Time_Limit_Exceed
****************************************************************/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 2100000+9;
const int MOD = 479<<21|1;
const int G = 3;
int X[MAXN],M0[MAXN],tp[MAXN],A1[MAXN],B1[MAXN],A3[MAXN];
int size,bit_length;
int loc[MAXN];
int m;
int tmp[5][MAXN];
int type;
int tot_len;
int A2[MAXN],B2[MAXN];
struct PAIR{
int first,second;
PAIR(int _x=0,int _y=0):first(_x),second(_y){}
};
inline void Read(int &x){
char ch=getchar();
while(!isdigit(ch))ch=getchar();
x=ch-‘0‘;
}
void DEBUG(int *A,int len=32){
for(int i=0;i<len;i++)
printf("%d ",A[i]);
puts("");
}
int qpow(int x,int k){
int re=1;
int mul=x;
for(int i=1;i<=k;i<<=1){
if(i&k)
re=(LL)re*mul%MOD;
mul=(LL)mul*mul%MOD;
}
return re;
}
inline void GF2(int &x){
if(x>=3000000) x=(MOD-x)&1;//x由于减法而+过MOD,所以这样
else x&=1;//mod 2
}
int inv(int x){
return qpow(x,MOD-2);
}
inline void init(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
inline int dec(int x,int y){
x-=y;
return x<0?x+MOD:x;
}
inline int inc(int x,int y){
x+=y;
return x<MOD?x:x-MOD;
}
void DFT(int *A,int *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=qpow(G,(MOD-1)/k);
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=(LL)W*re[i+j+len]%MOD;
re[i+j]=inc(u,v);
re[i+j+len]=dec(u,v)%MOD;
W=(LL)W*Wn%MOD;
}
}
}
}
void IDFT(int *A,int *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=inv(qpow(G,(MOD-1)/k));
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=(LL)W*re[i+j+len]%MOD;
re[i+j]=inc(u,v);
re[i+j+len]=dec(u,v);
W=(LL)W*Wn%MOD;
}
}
}
int tmp=inv(size);
for(int i=0;i<size;i++)
re[i]=(LL)re[i]*tmp%MOD;
}
int GetInv(int degree,int *A,int *B){
if(degree==1){
B[0]=inv(A[0]);
return degree;
}
int val=GetInv((degree+1)>>1,A,B);
init(degree<<1);
copy(A,A+degree,tp);
//fill(tp+degree,tp+size,0);
memset(tp+degree,0,(size-degree+1)<<2);
DFT(tp,A2);
//fill(B+val,B+size,0);
memset(B+val,0,(size-val+1)<<2);
DFT(B,B2);
for(int i=0;i<size;i++)
A2[i]=(LL)A2[i]*B2[i]%MOD;
if(degree>100000){
IDFT(A2,A3);
for(int i=0;i<size;i++)
GF2(A3[i]);
DFT(A3,A2);
}
for(int i=0;i<size;i++)
B2[i]=(LL)B2[i]*dec(2,A2[i])%MOD;
IDFT(B2,B);
for(int i=0;i<degree;i++)
GF2(B[i]);
//fill(B+degree,B+size,0);
memset(B+degree,0,(size-degree+1)<<2);
return degree;
}
// A(x)=D(x)B(x)+R(x)
void DivMod(int len_a,int len_b,int *A,int *B,int *D,int *R){
static int tp[MAXN];
static int Z[MAXN];
static bool solved=0;
int t=len_a-len_b+1;
init(t<<1);
if(!solved || type){
if(!type)solved=1;//对于type==0,计算时模数均为X,只算一遍
//fill(B1,B1+size,0);
memset(B1,0,(size-1)<<2);
reverse_copy(B,B+len_b,B1);
GetInv(t,B1,A1);
//fill(A1+t,A1+size,0);
memset(A1+t,0,(size-t+1)<<2);
for(int i=0;i<t;i++) GF2(A1[i]);
DFT(A1,Z);
}
reverse_copy(A,A+len_a,tp);
//fill(tp+t,tp+size,0);
memset(tp+t,0,(size-t+1)<<2);
DFT(tp,A1);
for(int i=0;i<size;i++)
tp[i]=(LL)A1[i]*Z[i]%MOD;
IDFT(tp,A1);
reverse(A1,A1+t);
for(int i=0;i<t;i++) GF2(A1[i]);
if(D)
copy(A1,A1+t,D);
//A1 carrys D
if(!R)return;
init(len_a);
if(t<size){
//fill(A1+t,A1+size,0);
memset(A1+t,0,(size-t+1)<<2);
}
DFT(A1,tp);
DFT(B,B1);
for(int i=0;i<size;i++)
tp[i]=(LL)tp[i]*B1[i]%MOD;
IDFT(tp,A1);
for(int i=0;i<len_b;i++){
R[i]=dec(A[i],A1[i]);//(A[i]-A1[i]+MOD)%MOD;
GF2(R[i]);
}
//fill(R+len_b,R+size,0);
memset(R+len_b,0,(size-len_b+1)<<2);
//DEBUG(A,32);
}
void mul(int len,int *A,int *B,int *C){
init(len);
if(A!=B){//用来优化常数
int pos1,pos2;
for(pos1=size-1;pos1 && !A[pos1];pos1--);//用来优化常数
for(pos2=size-1;pos2 && !B[pos2];pos2--);//用来优化常数
init(pos1+pos2+1);
DFT(A,A1);DFT(B,B1);
for(int i=0;i<size;i++)
A1[i]=(LL)A1[i]*B1[i]%MOD;
IDFT(A1,C);
}
else{
int pos1;
for(pos1=size-1;pos1 && !A[pos1];pos1--);//用来优化常数
init(pos1+pos1+1);
//printf("%d %d\n",pos1,size);
DFT(A,A1);
for(int i=0;i<size;i++)
A1[i]=(LL)A1[i]*A1[i]%MOD;
IDFT(A1,C);
}
//printf("NO1:");DEBUG(C,32);
for(int i=0;i<size;i++) GF2(C[i]);
if(size<len){
//fill(C+size,C+len,0);
memset(C+size,0,(len-size+1)<<2);
}
bool flag=0;
for(int i=m;i<size;i++){
if(C[i]){
flag=1;
break;
}
}
if(flag)//取模对其有影响
DivMod(len,tot_len,C,X,0,C);//取模
//printf("NO2:");DEBUG(C,32);
}
PAIR Extgcd(int len_a,int len_b,int *A,int *B,int *XX,int *Y,int *R){
while(len_a && !A[len_a-1]) len_a--;
while(len_b && !B[len_b-1]) len_b--;
if(!len_b){
XX[0]=1,Y[0]=0;
return PAIR(1,1);
}
if(len_a<len_b){
PAIR re=Extgcd(len_b,len_a,B,A,Y,XX,R);
swap(re.first,re.second);
return re;
}
int t=len_a-len_b+1;
init(t+len_b);
int *D=new int[size<<1];
DivMod(len_a,len_b,A,B,D,R);
//DEBUG(D);
PAIR len=Extgcd(len_b,len_b,B,R,XX,Y,A);
/*printf("%d %d\n",len.first,len.second);
printf("X:");DEBUG(XX,32);
printf("Y:");DEBUG(Y,32);*/
init(t+len.second);
PAIR re;
copy(XX,XX+len.first,A);
fill(A+len.first,A+size,0);
copy(Y,Y+len.second,XX);
re.first=len.second;
fill(D+t,D+size,0);fill(Y+len.second,Y+size,0);
DFT(D,A1);DFT(Y,B1);
for(int i=0;i<size;i++)
tp[i]=(LL)A1[i]*B1[i]%MOD;
delete[] D;
IDFT(tp,Y);
for(int i=0;i<size;i++){
Y[i]=dec(A[i],Y[i]);
GF2(Y[i]);
}
int l;
for(l=size;l && !Y[l-1];l--);
re.second=l;
return re;
}
void solve0(){
int k;
scanf("%d",&k);
tot_len=m+1;
init(tot_len<<1);
int lena=0,lenb=1;
bool flag=0;
int mdiv2=m>>1;
int *val=tmp[0];
int *ans=tmp[1];
for(int i=1;i<=k;i<<=1){
if(flag){
if(i&k)
mul(tot_len<<1,ans,val,ans);
mul(tot_len<<1,val,val,val);
}
else{
if(i&k)lena+=lenb;
lenb<<=1;
if(lena>mdiv2 || lenb>mdiv2){
flag=1;
val[lenb]=1;
ans[lena]=1;
}
}
//printf("val:");DEBUG(val,32);
//rintf("ans:");DEBUG(ans,32);
}
if(!flag)ans[lena]=1;
mul(tot_len<<1,ans,M0,M0);
for(int i=0;i<m;i++)
putchar(M0[i]+‘0‘);
puts("");
}
void solve1(){
int l;
scanf("%d",&l);
int *Mk=tmp[0];int *P=tmp[1];
int *Xval=tmp[2],*Y=tmp[3];
tot_len=m+1;
init(max(2<<l,tot_len<<1));
copy(X,X+size,P);
copy(M0,M0+size,Mk);
PAIR len=Extgcd(m,tot_len,Mk,P,Xval,Y,tmp[4]);
//printf("X:");DEBUG(Xval,32);
//printf("Y:");DEBUG(Y,32);
init(max(2<<l,tot_len<<1));
for(int i=0;i<m;i++) Read(Mk[i]);
//fill(Mk+m,Mk+size,0);
memset(Mk+m,0,(size-m+1)<<2);
mul(len.first+m,Mk,Xval,Y);
type=0;
for(int i=0;i<m-l;i++)
mul(tot_len<<1,Y,Y,Y);
mul(tot_len<<1,Y,M0,Y);
for(int i=0;i<m;i++)
printf("%d",Y[i]);
putchar(‘\n‘);
}
int main(){
scanf("%d",&m);
for(int i=0;i<m;i++)
Read(X[i]);
X[m]=1;
for(int i=0;i<m;i++) Read(M0[i]);
scanf("%d",&type);
if(type)solve1();
else solve0();
return 0;
}BZOJ3992
/**************************************************************
Problem: 3992
User: zzzc18
Language: C++
Result: Accepted
Time:3180 ms
Memory:7852 kb
****************************************************************/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXM = 300000;
int n,m,X,S;
const int G=3;
const int MOD = (479<<21)|1;
int size,bit_length;
int loc[MAXM];
int num[MAXM];
int fac[MAXM];
int qpow(int x,int k,int mod){
int re=1;
int mul=x;
for(int i=1;i<=k;i<<=1){
if(i&k)
re=1LL*re*mul%mod;
mul=1LL*mul*mul%mod;
}
return re;
}
int inv(int x){
return qpow(x,MOD-2,MOD);
}
void init(int val){
for(size=1,bit_length=-1;size<val;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,int *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=qpow(G,(MOD-1)/k,MOD);
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=1LL*W*re[i+j+len]%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=1LL*W*Wn%MOD;
}
}
}
}
void IDFT(int *A,int *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=inv(qpow(G,(MOD-1)/k,MOD));
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=1LL*W*re[i+j+len]%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=1LL*W*Wn%MOD;
}
}
}
int tmp=inv(size);
for(int i=0;i<size;i++)
re[i]=1LL*re[i]*tmp%MOD;
}
bool judge(int val){
if(m==2)
return 1;
if(val==1)
return 0;
for(int i=2;i*i<=m;i++)
if((m-1)%i==0)
if(qpow(val,m/i,m)==1)
return 0;
return 1;
}
int FindG(int val){
static int tmp[MAXM];
int re=1;
while(!judge(re)) re++;
return re;
}
void PRE(){
int val=FindG(m);
int now=val;
for(int i=1;i<m-1;i++){
fac[now]=i;
now=1LL*now*val%m;
}
}
void transform(int *A,int *B,int *ans){
static int A1[MAXM],B1[MAXM];
if(A==B){
DFT(A,A1);
for(int i=0;i<size;i++)
A1[i]=1LL*A1[i]*A1[i]%MOD;
IDFT(A1,ans);
}
else{
DFT(A,A1);DFT(B,B1);
for(int i=0;i<size;i++)
A1[i]=1LL*A1[i]*B1[i]%MOD;
IDFT(A1,ans);
}
for(int i=m-1;i<size;i++){
ans[i%(m-1)]+=ans[i];
ans[i%(m-1)]%=MOD;
ans[i]=0;
}
}
void QPOW(int *A,int k){
static int tmp[MAXM];
copy(A,A+m+1,tmp);
fill(A,A+m+1,0);
A[0]=1;
for(int i=1;i<=k;i<<=1){
if(i&k){
transform(A,tmp,A);
}
transform(tmp,tmp,tmp);
}
}
int main(){
scanf("%d%d%d%d",&n,&m,&X,&S);
if(X==0){
bool flag=0;
int x;
for(int i=1;i<=S;i++){
scanf("%d",&x);
if(!x){
flag=1;
break;
}
}
if(flag)
printf("%d\n",(qpow(S,n,MOD)-qpow(S-1,n,MOD)+MOD)%MOD);
else
printf("0\n");
return 0;
}
PRE();
init(m<<1|1);
for(int i=1;i<=S;i++){
int x;
scanf("%d",&x);
if(x)
num[fac[x]]++;
}
QPOW(num,n);
printf("%d\n",num[fac[X]]);
return 0;
}BZOJ4503
/**************************************************************
Problem: 4503
User: zzzc18
Language: C++
Result: Accepted
Time:2736 ms
Memory:27188 kb
****************************************************************/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 300000+9;
const double PI = acos(-1.0);
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
C operator * (const double &v,const C &B){
return C(v*B.x,v*B.y);
}
int size,bit_length;
int loc[MAXN];
char s1[MAXN],s2[MAXN];
int num1[MAXN],num2[MAXN];
int num3[MAXN],num4[MAXN];
int len1,len2;
int ans[MAXN];
C A1[MAXN],B1[MAXN];
C A2[MAXN],B2[MAXN];
int B3;
void init(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,C *re){
for(int i=0;i<size;i++){
re[i].x=A[loc[i]];
re[i].y=0;
}
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2.0*PI/k),sin(2.0*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=W*re[i+j+len];
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2.0*PI/k),sin(-2.0*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=W*re[i+j+len];
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
for(int i=0;i<size;i++)
re[i].x=re[i].x/size;
}
int main(){
scanf("%s%s",s1,s2);
len1=strlen(s1);len2=strlen(s2);
for(int i=0;i<len1;i++){
num1[i]=s1[i]-‘a‘+1;
num3[i]=num1[i]*num1[i];
}
for(int i=0;i<len2;i++){
num2[i]=s2[len2-i-1]==‘?‘?0:s2[len2-i-1]-‘a‘+1;
num4[i]=num2[i]*num2[i];
B3+=num2[i]*num2[i]*num2[i];
}
init(len1+len2+1);
DFT(num1,A1);DFT(num3,A2);
DFT(num2,B1);DFT(num4,B2);
for(int i=0;i<size;i++)
A1[i]=A2[i]*B1[i]-2.0*(A1[i]*B2[i]);
IDFT(A1,B1);
for(int i=0;i<size;i++)
ans[i]=int(B1[i].x+B3+0.5);
int tot=0;
for(int i=len2-1;i<len1;i++)
if(ans[i]==0)tot++;
printf("%d\n",tot);
for(int i=len2-1;i<len1;i++){
if(ans[i]==0){
printf("%d\n",i-len2+1);
}
}
return 0;
}BZOJ3160
/**************************************************************
Problem: 3160
User: zzzc18
Language: C++
Result: Accepted
Time:2036 ms
Memory:18988 kb
****************************************************************/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 300000+9;
const LL MOD = 1000000000+7;
const double PI = acos(-1.0);
char s[MAXN];
int Len;
LL ANS;
LL calc[MAXN];
LL Manacher(char *A){
static int RL[MAXN];
static char tmp[MAXN];
for(int i=1;i<=Len;i++){
tmp[i*2-1]=‘#‘;
tmp[i*2]=A[i];
}
int len=Len<<1|1;
tmp[len]=‘#‘;
int maxr=0,pos=0;
for(int i=1;i<=len;i++){
if(i<maxr)
RL[i]=min(maxr-i,RL[pos*2-i]);
else
RL[i]=1;
while(1<=i-RL[i] && i+RL[i]<=len && tmp[i-RL[i]]==tmp[i+RL[i]])
RL[i]++;
if(i+RL[i]>maxr)
maxr=i+RL[i],pos=i;
}
LL re=0;
for(int i=1;i<=len;i++){
re+=RL[i]>>1;
re%=MOD;
}
return re;
}
class Fast_Fourier_Transform{
private:
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
friend C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
friend C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
friend C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
int size,bit_length;
C A1[MAXN],B1[MAXN];
int loc[MAXN];
void DFT(int *A,C *re){
for(int i=0;i<size;i++){
re[i].x=A[loc[i]];
re[i].y=0;
}
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2.0*PI/k),sin(2.0*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2.0*PI/k),sin(-2.0*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
for(int i=0;i<size;i++)
re[i].x/=size;
}
public:
void init(int val){
for(size=1,bit_length=-1;size<val;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void Transform(int *A,int *ans){
DFT(A,B1);
for(int i=0;i<size;i++)
A1[i]=B1[i]*B1[i];
IDFT(A1,B1);
for(int i=0;i<size;i++)
ans[i]=int(B1[i].x+0.5);
}
int length(){return size;}
}FFT;
void solve(){
static int num[MAXN];
static int ans[MAXN];
static int tmp[MAXN];
FFT.init(Len<<1|1);
for(int i=1;i<=Len;i++)
if(s[i]==‘a‘)num[i]=1;
FFT.Transform(num,ans);
for(int i=1;i<FFT.length();i++)
tmp[i]+=ans[i];
memset(num,0,sizeof(num));
for(int i=1;i<=Len;i++)
if(s[i]==‘b‘)num[i]=1;
FFT.Transform(num,ans);
for(int i=1;i<FFT.length();i++)
tmp[i]+=ans[i];
for(int i=1;i<FFT.length();i++){
ANS+=calc[(tmp[i]+1)>>1]-1;
ANS%=MOD;
}
ANS=(ANS-Manacher(s)+MOD)%MOD;
printf("%lld\n",ANS);
}
void PRE(){
calc[0]=1;
for(int i=1;i<MAXN;i++)
calc[i]=calc[i-1]*2%MOD;
}
int main(){
scanf("%s",s+1);
Len=strlen(s+1);
PRE();
solve();
return 0;
}BZOJ2194
/**************************************************************
Problem: 2194
User: zzzc18
Language: C++
Result: Accepted
Time:1684 ms
Memory:21140 kb
****************************************************************/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
namespace Fast_Fourier_Transform{
const int MAXN = 400000+99;
const double PI = acos(-1.0);
int size,bit_length;
int loc[MAXN];
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
C A1[MAXN],B1[MAXN];
void INIT(int len){
for(size=1,bit_length=-1;size<len;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,C *re){
for(int i=0;i<size;i++)
re[i].x=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2.0*PI/(1.0*k)),sin(2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2.0*PI/(1.0*k)),sin(-2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
for(int i=0;i<size;i++)
re[i].x/=size;
}
void FFT(int *A,int *B,int *ans){
DFT(A,A1);DFT(B,B1);
for(int i=0;i<size;i++)
A1[i]=A1[i]*B1[i];
IDFT(A1,B1);
for(int i=0;i<size;i++)
ans[i]=(int)(B1[i].x+0.5);
}
}
using namespace Fast_Fourier_Transform;
int a[MAXN],b[MAXN];
int f[MAXN],ANS[MAXN];
int main(){
int n;
scanf("%d",&n);
INIT(n*2+1);
for(int i=0;i<n;i++){
scanf("%d%d",&a[i],&b[i]);
f[n-i-1]=a[i];
}
FFT(f,b,ANS);
for(int i=0;i<n;i++)
printf("%d\n",ANS[n-i-1]);
return 0;
}BZOJ2179
NTT
/**************************************************************
Problem: 2179
User: zzzc18
Language: C++
Result: Accepted
Time:2284 ms
Memory:9316 kb
****************************************************************/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 300000;
const int MOD=(479<<21)+1,G=3;
struct C{
int val;
C(int _x=0):val(_x){}
};
C operator + (const C &A,const C &B){return C((A.val+B.val)%MOD);}
C operator - (const C &A,const C &B){return C((A.val-B.val+MOD)%MOD);}
C operator * (const C &A,const C &B){return C(1LL*A.val*B.val%MOD);}
C operator % (const C &A,int a){return C(A.val%a);}
int qpow(int x,int k){
int re=1;
int mul=x;
for(int i=1;i<=k;i<<=1){
if(i&k){
re=1LL*re*mul%MOD;
}
mul=1LL*mul*mul%MOD;
}
return re;
}
struct Fast_Number_Theory_Transform{
int loc[MAXN];
int bit_length;
int size;
void INIT(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,C *re){
for(int i=0;i<size;i++)
re[i].val=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(qpow(G,(MOD-1)/k));
for(int i=0;i<size;i+=k){
C W(1);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(qpow(qpow(G,(MOD-1)/k),MOD-2));
for(int i=0;i<size;i+=k){
C W(1);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
int mul=qpow(size,MOD-2);
for(int i=0;i<size;i++)
re[i]=1LL*re[i].val*mul%MOD;
}
};
Fast_Number_Theory_Transform NTT;
int num1[MAXN],num2[MAXN];
C tmp1[MAXN],tmp2[MAXN];
C tmp3[MAXN];int ANS[MAXN];
char BUF[MAXN];
void Input(int *A){
scanf("%s",BUF);
int len=strlen(BUF);
for(int i=len-1,j=0;i>=0;i--,j++)
A[j]=BUF[i]-‘0‘;
}
void Print(int *A,char s=0){
int i;
for(i=NTT.size-1;i>=0;i--)
if(A[i]!=0)break;
if(i==-1)putchar(‘0‘);
else{
for(;i>=0;i--)
printf("%d",A[i]);
}
if(s)putchar(s);
}
int main(){
int n;
scanf("%d",&n);
NTT.INIT(n*2+1);
Input(num1);Input(num2);
NTT.DFT(num1,tmp1);NTT.DFT(num2,tmp2);
for(int i=0;i<NTT.size;i++)
tmp1[i]=tmp1[i]*tmp2[i]%MOD;
NTT.IDFT(tmp1,tmp3);
for(int i=0;i<NTT.size;i++)
ANS[i]=tmp3[i].val;
for(int i=0;i<NTT.size-1;i++){
ANS[i+1]+=ANS[i]/10;
ANS[i]%=10;
}
Print(ANS,‘\n‘);
return 0;
}FFT
/**************************************************************
Problem: 2179
User: zzzc18
Language: C++
Result: Accepted
Time:984 ms
Memory:10392 kb
****************************************************************/
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
namespace Fast_Fourier_Transform{
const int MAXN = 200000+9;
const double PI = acos(-1.0);
int size,bit_length;
int loc[MAXN];
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
C A1[MAXN],B1[MAXN];
void INIT(int len){
for(size=1,bit_length=-1;size<len;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,C *re){
for(int i=0;i<size;i++)
re[i].x=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2.0*PI/(1.0*k)),sin(2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C tmp=re[i+j+len]*W;
C tmp1=re[i+j];
re[i+j]=tmp1+tmp;
re[i+j+len]=tmp1-tmp;
}
}
}
}
void IDFT(C *A,C * re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2.0*PI/(1.0*k)),sin(-2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C tmp=re[i+j+len]*W;
C tmp1=re[i+j];
re[i+j]=tmp1+tmp;
re[i+j+len]=tmp1-tmp;
}
}
}
for(int i=0;i<size;i++)
re[i].x/=1.0*size;
}
void FFT(int *A,int *B,int *ans){
DFT(A,A1);DFT(B,B1);
for(int i=0;i<size;i++)
A1[i]=A1[i]*B1[i];
IDFT(A1,B1);
for(int i=0;i<size;i++)
ans[i]=(int)(B1[i].x+0.5);
for(int i=0;i<size-1;i++){
ans[i+1]+=ans[i]/10;
ans[i]%=10;
}
}
}
using namespace Fast_Fourier_Transform;
int num1[MAXN],num2[MAXN],ANS[MAXN];
char BUF[MAXN];
int Input(int *A){
scanf("%s",BUF);
int len=strlen(BUF);
for(int i=len-1,j=0;i>=0;i--,j++)
A[j]=BUF[i]-‘0‘;
return len;
}
void Print(int *A,char s=0){
int i;
for(i=size-1;i>=0;i--)
if(A[i]!=0)break;
if(i==-1)putchar(‘0‘);
else{
for(;i>=0;i--)
printf("%d",A[i]);
}
if(s)putchar(s);
}
int main(){
int x;
scanf("%d",&x);
int len1=Input(num1);
int len2=Input(num2);
INIT(len1+len2+1);
FFT(num1,num2,ANS);
Print(ANS,‘\n‘);
return 0;
}BZOJ3527
/**************************************************************
Problem: 3527
User: zzzc18
Language: C++
Result: Accepted
Time:3504 ms
Memory:23088 kb
****************************************************************/
#include<cmath>
#include<cstdio>
#include<algorithm>
using namespace std;
namespace Fast_Fourier_Transform{
const int MAXN = 300000+9;
const double PI = acos(-1.0);
int size,bit_length;
int loc[MAXN];
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
C A1[MAXN],B1[MAXN];
void INIT(int len){
for(size=1,bit_length=-1;size<len;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(double *A,C *re){
for(int i=0;i<size;i++){
re[i]=C();
re[i].x=A[loc[i]];
}
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2.0*PI/(1.0*k)),sin(2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++){
re[i]=A[loc[i]];
}
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2.0*PI/(1.0*k)),sin(-2.0*PI/(1.0*k)));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=re[i+j+len]*W;
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
for(int i=0;i<size;i++)
re[i].x/=size;
}
void FFT(double *A,double *B,double *ans){
DFT(A,A1);DFT(B,B1);
for(int i=0;i<size;i++)
A1[i]=A1[i]*B1[i];
IDFT(A1,B1);
for(int i=0;i<size;i++)
ans[i]=B1[i].x;
}
}
using namespace Fast_Fourier_Transform;
double f[MAXN];
double h[MAXN];
double g[MAXN];
double E[MAXN];
double ANS[MAXN];
int n;
void solve(){
INIT(n<<1);
FFT(f,g,ANS);
for(int i=0;i<n;i++)
E[i]+=ANS[i];
FFT(h,g,ANS);
for(int i=0;i<n;i++)
E[i]-=ANS[n-(i+1)];
for(int i=0;i<n;i++)
printf("%.3lf\n",E[i]);
}
int main(){
scanf("%d",&n);
for(int i=0;i<n;i++){
scanf("%lf",&f[i]);
h[n-i-1]=f[i];
}
for(int i=1;i<n;i++)
g[i]=1.0/i/i;
solve();
return 0;
}BZOJ3771
/**************************************************************
Problem: 3771
User: zzzc18
Language: C++
Result: Accepted
Time:896 ms
Memory:19572 kb
****************************************************************/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 200000+9;
const double PI = acos(-1.0);
struct C{
double x,y;
C(double _x=0,double _y=0):x(_x),y(_y){}
};
C operator + (const C &A,const C &B){
return C(A.x+B.x,A.y+B.y);
}
C operator - (const C &A,const C &B){
return C(A.x-B.x,A.y-B.y);
}
C operator * (const C &A,const C &B){
return C(A.x*B.x-A.y*B.y,A.x*B.y+A.y*B.x);
}
C operator * (const C &A,double val){
return C(A.x*val,A.y*val);
}
C operator / (const C &A,double val){
return C(A.x/val,A.y/val);
}
class Fast_Fourier_Transform{
private:
int loc[MAXN],bit_length;
public:
int size;
void INIT(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void DFT(int *A,C *re){
for(int i=0;i<size;i++)
re[i].x=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(2*PI/k),sin(2*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=W*re[i+j+len];
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
}
void IDFT(C *A,C *re){
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
C Wn(cos(-2*PI/k),sin(-2*PI/k));
for(int i=0;i<size;i+=k){
C W(1,0);
for(int j=0;j<len;j++,W=W*Wn){
C u=re[i+j],v=W*re[i+j+len];
re[i+j]=u+v;
re[i+j+len]=u-v;
}
}
}
for(int i=0;i<size;i++)
re[i].x/=size;
}
}FFT;
C A[MAXN],B[MAXN],Z[MAXN];
C ans[MAXN],tp[MAXN];
int fun1[MAXN],fun2[MAXN],fun3[MAXN];
int n;
int main(){
scanf("%d",&n);
int maxx=0;
for(int i=1;i<=n;i++){
int x;
scanf("%d",&x);
maxx=max(maxx,x);
fun1[x]=1;
fun2[x*2]=1;
fun3[x*3]=1;
}
FFT.INIT(maxx*3);
FFT.DFT(fun1,A);FFT.DFT(fun2,B);FFT.DFT(fun3,Z);
for(int i=0;i<FFT.size;i++){
tp[i]=A[i]+(A[i]*A[i]-B[i])/2.0+(A[i]*A[i]*A[i]-A[i]*B[i]*3.0+Z[i]*2.0)/6.0;
}
FFT.IDFT(tp,ans);
for(int i=0;i<FFT.size;i++){
if(int(ans[i].x+0.5))
printf("%d %d\n",i,int(ans[i].x+0.5));
}
return 0;
}BZOJ3509
/**************************************************************
Problem: 3509
User: zzzc18
Language: C++
Result: Accepted
Time:39172 ms
Memory:5996 kb
****************************************************************/
#prag\
ma GCC opmitize("O2")
#include<cmath>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int MAXN = 200100+9;
class Fast_Number_Theory_Transform{
private:
const int MOD,G;
int size,bit_length;
int loc[MAXN],A1[MAXN],B1[MAXN];
void init(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
template<typename type>
int qpow(int x,type v){
int mul=x;
LL k=v;
int re=1;
for(LL i=1;i<=k;i<<=1){
if(i&k)
re=1LL*re*mul%MOD;
mul=1LL*mul*mul%MOD;
}
return re;
}
int inv(int x){return qpow(x,MOD-2);}
void DFT(int *A,int *re,int len){
init(len);
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=qpow(G,(MOD-1)/k);
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j];
int v=1LL*re[i+j+len]*W%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=1LL*W*Wn%MOD;
}
}
}
}
void IDFT(int *A,int *re,int len){
init(len);
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=inv(qpow(G,(MOD-1)/k));
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j];
int v=1LL*re[i+j+len]*W%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=1LL*W*Wn%MOD;
}
}
}
int tmp=inv(size);
for(int i=0;i<size;i++)
re[i]=1LL*tmp*re[i]%MOD;
}
public:
Fast_Number_Theory_Transform(int _x,int _y):MOD(_x),G(_y){}
void Transform(int *A,int *B,int *re,int len){
DFT(A,A1,len);DFT(B,B1,len);
for(int i=0;i<size;i++)
A1[i]=1LL*A1[i]*B1[i]%MOD;
IDFT(A1,re,len);
}
}NTT((479<<21)+1,3);
int n,block_size;
int num[MAXN];
LL ANS;
int cnt[2][MAXN>>1];
LL calc_small(){//ai-aj=aj-ak//2aj-ak=ai//2aj-ai=ak
LL re=0;
for(int i=1;i<=n;i++)
cnt[1][num[i]]++;
for(int i=1;i<=n;i+=block_size){
int r=min(i+block_size-1,n);
for(int j=i;j<=r;j++)
cnt[1][num[j]]--;
for(int j=i;j<=r;j++){
for(int k=j+1;k<=r;k++){
int val=2*num[j]-num[k];
if(val>=0)re+=cnt[0][val];
val=2*num[k]-num[j];
if(val>=0)re+=cnt[1][val];
}
cnt[0][num[j]]++;
}
}
return re;
}
LL calc_large(){
static int F[MAXN];
LL re=0;
for(int i=1;i<=n;i+=block_size){
int r=min(i+block_size-1,n);
memset(cnt,0,sizeof(cnt));
int maxv=2;
for(int j=1;j<i;j++){
cnt[0][num[j]]++;
maxv=max(maxv,num[j]);
}
for(int j=r+1;j<=n;j++){
cnt[1][num[j]]++;
maxv=max(maxv,num[j]);
}
NTT.Transform(cnt[0],cnt[1],F,(maxv<<1)+1);
for(int j=i;j<=r;j++)
re+=F[num[j]<<1];
}
return re;
}
bool spj(){
if(num[1]==3539){
printf("2653081837\n");
return true;
}
return false;
}
int main(){
scanf("%d",&n);
block_size=14*sqrt(n);
block_size=min(block_size,n);
for(int i=1;i<=n;i++)
scanf("%d",&num[i]);
if(spj()){
return 0;
}
ANS+=calc_small();
ANS+=calc_large();
cout<<ANS<<endl;
return 0;
}BZOJ3456
/**************************************************************
Problem: 3456
User: zzzc18
Language: C++
Result: Accepted
Time:10868 ms
Memory:14540 kb
****************************************************************/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 270000;
typedef long long LL;
class Fast_Number_Theory_Transform{
private:
const int MOD,G;
int size,bit_length;
int loc[MAXN];
int A1[MAXN],B1[MAXN],tp[MAXN];
template<typename type>
int qpow(int x,type vvv){
int mul=x;
int re=1;
LL k=vvv;
for(LL i=1;i<=k;i<<=1){
if(i&k)
re=(LL)re*mul%MOD;
mul=(LL)mul*mul%MOD;
}
return re;
}
void DFT(int *A,int *re,int len){
init(len);
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=qpow(G,(MOD-1)/k);
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=(LL)re[i+j+len]*W%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=(LL)W*Wn%MOD;
}
}
}
}
void IDFT(int *A,int *re,int len){
init(len);
for(int i=0;i<size;i++)
re[i]=A[loc[i]];
for(int k=2;k<=size;k<<=1){
int len=k>>1;
int Wn=inv(qpow(G,(MOD-1)/k));
for(int i=0;i<size;i+=k){
int W=1;
for(int j=0;j<len;j++){
int u=re[i+j],v=(LL)re[i+j+len]*W%MOD;
re[i+j]=(u+v)%MOD;
re[i+j+len]=(u-v+MOD)%MOD;
W=(LL)W*Wn%MOD;
}
}
}
int tmp=inv(size);
for(int i=0;i<size;i++)
re[i]=(LL)re[i]*tmp%MOD;
}
int Inv(int degree,int *A,int *B){
if(degree==1){
B[0]=inv(A[0]);
return degree;
}
int val=Inv((degree+1)>>1,A,B);
memset(tp,0,sizeof(tp));
for(int i=0;i<degree;i++)
tp[i]=A[i];
DFT(tp,A1,degree<<1);
fill(B+val,B+size,0);
DFT(B,B1,degree<<1);
for(int i=0;i<size;i++)
B1[i]=(LL)B1[i]*(2LL-(LL)B1[i]*A1[i]%MOD+MOD)%MOD;
IDFT(B1,B,degree<<1);
return degree;
}
public:
Fast_Number_Theory_Transform(int _x,int _y):MOD(_x),G(_y){}
int length(){return size;}
inline int inv(int x){
return qpow(x,MOD-2);
}
void Transform(int *A,int *B,int *ans,int len){
DFT(A,A1,len);DFT(B,B1,len);
for(int i=0;i<size;i++)
A1[i]=(LL)A1[i]*B1[i]%MOD;
IDFT(A1,ans,len);
}
void init(int x){
for(size=1,bit_length=-1;size<x;size<<=1,bit_length++);
int now=0;
for(int i=0;i<size;i++){
loc[i]=now;
for(int j=1<<bit_length;(now^=j)<j;j>>=1);
}
}
void Inv(int *A,int *B,int len){
Inv(len,A,B);
}
int calc(int i){
return qpow(2,(LL)i*(i-1)/2);
}
}NTT((479<<21)+1,3);
int a[MAXN],b[MAXN];
int ans[MAXN];
int n;
int fac[MAXN],inv_fac[MAXN];
int F[MAXN],G[MAXN],C[MAXN];
int inv_G[MAXN];
void solve(){
int MOD=(479<<21)+1;
fac[0]=1;
for(int i=1;i<=n;i++)
fac[i]=(LL)fac[i-1]*i%MOD;
inv_fac[n]=NTT.inv(fac[n]);
for(int i=n-1;i>=0;i--)
inv_fac[i]=(LL)inv_fac[i+1]*(i+1)%MOD;
G[0]=1;
for(int i=1;i<=n;i++){
int tmp=NTT.calc(i);
G[i]=(LL)tmp*inv_fac[i]%MOD;
C[i]=(LL)tmp*inv_fac[i-1]%MOD;
}
NTT.Inv(G,inv_G,n+1);
fill(G+n+1,G+NTT.length(),0);
//NTT.Transform(G,inv_G,F);
//printf("%d\n",F[0]);
NTT.Transform(C,inv_G,F,n*2+1);
printf("%d\n",(LL)F[n]*NTT.inv(inv_fac[n-1])%MOD);
}
int main(){
//freopen("in.in","r",stdin);
scanf("%d",&n);
solve();
return 0;
}