BOI‘98 DAY 2 TASK 1
CONFERENCE CALL
PROBLEM
A telecom company would like to offer a three-party conference call service. This service enables three customers to participate in a telephone conversation simultaneously. A customer accesses the interconnection network of the telephone system via a switch. The network consists of switches linked by bidirectional lines. Over the existing network, the three participants accessing the network via three different switches, must be connected with the minimum cost. Note that it is possible to connect any two switches. You will be given all the links between the switches of the network along with their associated costs. You are requested to find the connections which will minimize the total cost of interconnecting the three switches to which the participants in a conference call are connected.
INPUT
The input is a text file named conf.inp. The first line contains two numbers : The number of switches, designated by ( N <= 100) and the number of switch-to-switch links in the network, designated by E, separated by a blank. Each of the following E input lines contains three integers, designated by i, j and ci,j where i and j are the numbers of two different switches and ci,jis the cost of using the link between i and j in a conference call (1 <= ci,j<= 100), each separated by one blank. The last line of input contains three integers, which designate the three switches that participate in the conference call, each separated by one blank. The switches are identified with integers 1 through N consecutively.
OUTPUT
The output must be a text file named conf.out. The first line must contain the total (minimal) cost of establishing a conference call among the given three switches and the number R of switch-to-switch connections needed to establish this conference call, separated by a blank. Each of the following R lines must contain two integers, which denote that the link between the switch numbered by the first integer and the switch numbered by the second integer is included in the solution -ordering of between the two switches is not important. The ordering among the last R lines of the output is also not important.
EXAMPLE
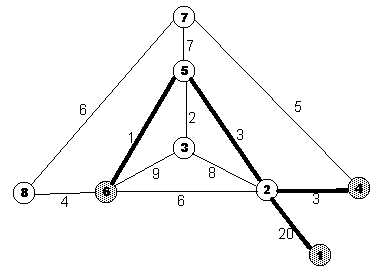
分析
这道题可以形象地理解成。班里有45个同学,其中有三个同学想要选某一个同学家作为见面地点,要求这个见面地点到三个同学家的距离和最小。
容易想到运用单源最短路算法,分别以三个客户端作为源点,运行最短路算法。把距离保存在三个数组当中。最后循环每一个点,查哪一个点到三个点的距离和最短。保存这个点t,这个最小费用s。
最后从t开始反向查找会经过的每一条边。
程序
1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 int n, m, EdgeCount, u, v, w, a[3], f[3][105], Head[105], pre[3][105], t, k, s; 6 struct node 7 { 8 int Next, Aim, Weight; 9 }Edge[20005]; 10 struct h 11 { 12 int len,point; 13 bool operator < (const struct h &x) const 14 { 15 return x.len<len; 16 } 17 bool operator > (const struct h &x) const 18 { 19 return x.len>len; 20 } 21 }; 22 struct p 23 { 24 int x,y; 25 bool operator > (const struct p &P) const 26 { 27 return (P.x<x)||((P.x==x)&&(P.y<y)); 28 } 29 bool operator < (const struct p &P) const 30 { 31 return (P.x>x)||((P.x==x)&&(P.y>y)); 32 } 33 }b[20005]; 34 35 inline void Insert(int u, int v, int w) 36 { 37 Edge[++EdgeCount]=(node){Head[u],v,w}; 38 Head[u]=EdgeCount; 39 } 40 41 void Dijkstra(int num,int st) 42 { 43 priority_queue<h> Q; 44 f[num][st]=0; 45 while(!Q.empty()) Q.pop(); 46 Q.push((struct h){0,st}); 47 for (int j=1;j<=n;j++) 48 { 49 struct h x=Q.top(); 50 Q.pop(); 51 for (int i=Head[x.point];i;i=Edge[i].Next) 52 if (f[num][x.point]+Edge[i].Weight<f[num][Edge[i].Aim]) 53 { 54 f[num][Edge[i].Aim]=f[num][x.point]+Edge[i].Weight; 55 Q.push((struct h){f[num][Edge[i].Aim],Edge[i].Aim}); 56 pre[num][Edge[i].Aim]=x.point; 57 } 58 } 59 } 60 61 int main() 62 { 63 freopen("conference.in","r",stdin); 64 freopen("conference.out","w",stdout); 65 cin >> n >> m; 66 EdgeCount=0; 67 for (int i = 1; i <= m; i++) 68 { 69 cin >> u >> v >> w; 70 Insert(u, v, w); 71 Insert(v, u, w); 72 } 73 memset(f, 0x3f, sizeof(f)); 74 for (int i = 0; i <= 2; i++) 75 { 76 cin>>a[i]; 77 Dijkstra(i,a[i]); 78 } 79 s=1e+8; 80 for (int i = 1; i <= n; i++) 81 if (s > f[0][i]+f[1][i]+f[2][i]) 82 { 83 s = f[0][i]+f[1][i]+f[2][i]; 84 t = i; 85 } 86 cout << s; 87 s = 0; 88 for (int i = 0; i <= 2; i++) 89 { 90 k = t; 91 while (pre[i][k] != 0) 92 { 93 b[++s] = (p){min(pre[i][k],k),max(pre[i][k],k)}; 94 k = pre[i][k]; 95 } 96 } 97 sort(b+1,b+(s+1)); 98 t = 1; 99 for (int i = 2; i <= s; i++) 100 if (b[i].x != b[i-1].x || b[i].y != b[i-1].y) 101 t++; 102 cout << " " << t << endl; 103 cout << b[1].x << " " << b[1].y << endl; 104 for (int i=2;i<=s;i++) 105 if (b[i].x != b[i-1].x || b[i].y != b[i-1].y) 106 cout<<b[i].x<<" "<<b[i].y<<endl; 107 return 0; 108 }
