矩阵快速幂+费马小定理
矩阵也是可以跑费马小定理的,但是要注意这个:
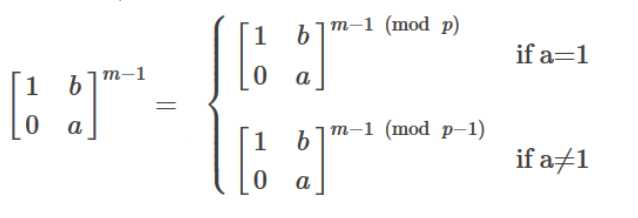
(图是盗来的QAQ)
就是说如果矩阵a[i][i]都是相等的,那么就是mod p 而不是mod p-1了
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<vector>
#include<cmath>
#define MOD 1000000007
#define MAXN 1000000+10
#define ll long long
#define pb push_back
#define ft first
#define sc second
#define mp make_pair
using namespace std;
char s1[MAXN],s2[MAXN];
int n,m;
int a,b,c,d,p;
struct Mat{
int a[2][2];
Mat(){
memset(a,0,sizeof(a));
}
friend Mat operator * (const Mat &A,const Mat B){
Mat C;
for(int i=0;i<2;i++){
for(int j=0;j<2;j++){
for(int k=0;k<2;k++){
C.a[i][j]+=(1LL*A.a[i][k]*B.a[k][j]%MOD);
C.a[i][j]%=MOD;
}
}
}
return C;
}
friend Mat operator ^ (Mat A,int p){
Mat B;
B.a[0][0]=B.a[1][1]=1;
while(p){
if(p&1){
B=B*A;
}
A=A*A;
p>>=1;
}
return B;
}
};
void solve(){
scanf("%s%s",s1+1,s2+1);
scanf("%d%d%d%d",&a,&b,&c,&d);
p=MOD-1+(a==1);
int len=strlen(s2+1);
for(int i=1;i<=len;i++){
m=(1LL*m*10+s2[i]-‘0‘)%p;
}
m--;if(m<0)m+=p;
Mat A;
A.a[0][0]=a,A.a[0][1]=b,A.a[1][1]=1;
Mat B;
B=A^m;
Mat C;
C=B;
A.a[0][0]=c,A.a[0][1]=d,A.a[1][1]=1;
C=C*A;
p=MOD-1+(C.a[0][0]==C.a[1][1]);
len=strlen(s1+1);
for(int i=1;i<=len;i++){
n=(1LL*n*10+s1[i]-‘0‘)%p;
}
n--;if(n<0)n+=p;
C=C^n;
C=C*B;
int ans=(C.a[0][0]+C.a[0][1])%MOD;
printf("%d\n",ans);
}
int main()
{
//freopen("data.in","r",stdin);
solve();
return 0;
}
