BAB(Branch.and.Band)算法是由Nick Roussopoulousnl等人于1995年提出的,是最早的基于R.树的静态最近邻查询算法。该算法使用MINDIST和MINMAXDIST两个距离作为查询过程中的判断条件,对R树进行深度优先
搜索以查找最近邻,适用于基于静态对象的最近邻搜索。BAB思想已经被广泛的应用于人工智能以及运筹学等领域。如果搜索顺序和剪枝的规则选取适当,可以有效的减少系统在大规模空间搜索过程中的结点访问数目。
一、The MBR Face Property
Lemma:Every face of any MBR contains at least one point of an actual spatial object 如图:
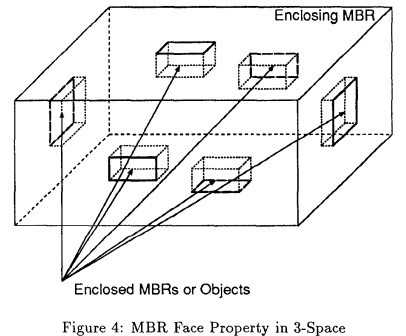
二、距离度量MINDIST和MINMAXDIST
为了减少计算量,文中的距离都以实际欧式距离的平方为标准。
给定一个查询点p及包含在一个MBR中的空间数据对象O,定义两个距离MINDIST和MINMAXDIST作为最近邻的度量和约束。其中:
MINDIST(P,R): the shortest distance from P to R
MINMAXDIST(P,R):the minimum over all dimensions distance from P to the furthest point of the closest face of the R
Theorem:
1. Any object O in R has distance from P that is at least as large as MINDIST
2.There exists at least one object within R with distance <= to MINMAXDIST
so:
MINDIST(P,R) <= NN(P) <= MINMAXDIST(P,R) (1)
三、MINDIST和MINMAXDIST的计算
MINDIST:
1.查询点p在R内或R的边界上则MINDIST=0
2.查询点p在R外,若最短距离距离(p到R的边)存在,则MINDIST=p到R的边的最短距离
否则,MINDIST=p到R的顶点的最短最短距离。
MINMAXDIST的计算过程:
1.找出与第k轴垂直的并且离查询点p最近的面,记为H
2.选择从查询点p到面H中距离最远的那个点,记为a
3.计算查询点p到点a的距离,记为dk
4.对每个坐标轴重复步骤1-步骤3,记计算所得距离为d1,d2,...dk
5.从所有计算所得距离中选出最小的那一个,即MINMAXDIST
例如:下图中查询点p在外接矩形R之外,根据上面的计算步骤我们可得: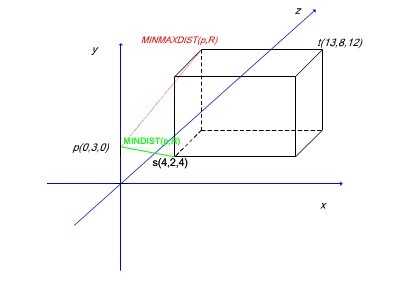
X轴:找到点(4,8,12) 计算p到此点的距离的平方dx=185
y轴:找到点(13,2,12) 计算p到此点的距离的平方dy=313
z轴:找到点(13,8,4) 计算p到ci点的距离的平方dz=210
所以此例中的MINMAXDIST(p,R)=185
下图表示了二维空间中点P与几个最小包含矩形MBR的MINDIST和MINMAXDIST的一个例子。二维空间中共有四个MBR,点P到它们的MINDIST和MINMAxDIST值在图中用箭头标出。如果点P位于MBR内部MINDIST值为0。
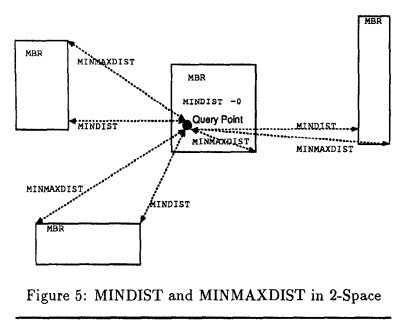
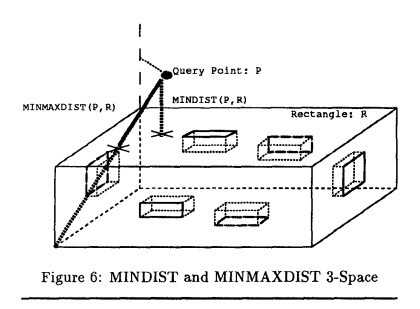
下图表示了三维空间中的MINDIST和MINMAXDIST。
四、减枝策略
由以上讨论,剪枝过程按以下三种策略进行:
1.若一个最小包含矩形E的MINDIST值大于另一个最小包含矩形E’的MINMAXDIST值,则最小包含矩形E内不可能包含最近邻对象。所以E可以被忽略。该策略用于向下剪枝。
2.若查询点q到某对象O的距离值大于点q到最小包含矩形E的MINMAXDIST的值则对象O被丢弃。因为最小包含矩形层此时包含距离查询点口更近的对象O’。该策略用于向上剪枝。
3.若最小包含矩形E的MINDIST值大于查询点g到某对象O的距离,则E被丢弃,因为最小包含矩形E内部不可能包含比对象O更近的对象。该策略用于向上剪枝。
尽管规定在向下剪枝时用MINMAXDIST进行判断,然而在某些情况下使用MINDIST效果会更好。例如当R树的结点中不存在死区或者死区很少时,在R树的某一层上MINDIST相对于MINMAxDIST而言是查询点到最近邻对象实际距离的更好估计。此时使用MINDIST可以剪掉更多无关的候选MBR。
五、Branch and Bound算法
该算法从根结点开始向下访问各层MBR。算法中首先假定最近邻距离Nearest为无穷大。随着搜索的下降,对每个最新访问的非叶结点首先计算出其中所有的MBR的MINDIST值,并将这些值排序后放入活动分支链表ABL(Active Branch List)中,接着对ABL运用剪枝策略1和策略2来移除不必要的分支。算法在ABL上重复进行直至ABL为空。每次重复过程中都选择链表中的下一个分支,并在与该分支的MBR相应的结点上递归进行以上过程。对于叶结点算法对每个对象调用一个特定类型的距离函数,并将计算出的值逐个与Nearest比较,选择其中更小的值替换Nearest。在递归过程返回时使用这个新的最近邻距离的估计值作为判断条件,采用策略3剪枝以移除ABL中所有MINDIST值大子Nearest的MBR所在的分支。
算法伪代码:

参考:
Nearest Neighborhood Queries.Nick Roussopoulos等.
http://www.doc88.com/p-146668818114.html
http://zh.scribd.com/doc/73414427/32/Fig-4-4-Example-of-MINDIST-and-MINMAXDIST
