题意:给一棵带边权的树,按给定的顺序删掉所有边,每删一条边,输出权值$w$,并把小的那块全部乘$w$,大的那块全部加$w$,强制在线
原题是sgu的,但现在sgu好像挂了,幸运地在codeforces gym里面找到这个题(题号是K)
本来这个并不是数据结构题,按题解的说法应该是用一些奇技淫巧转化一下,但为了好玩我还是写了个伪ETT练一下手
ETT全名是Euler Tour Tree,顾名思义就是用平衡树维护欧拉遍历序
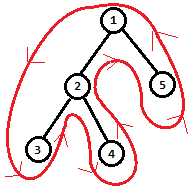
对于这棵树,欧拉遍历序就是123242151,虽然它是一个环,但通常约定在根节点处断开,方便实现
这题是存边权,所以在欧拉序列$E_{1\cdots 2n-1}$中,第$i$位存$(E_i,E_{i+1})$这条边的权值
考虑删边,假设原来的根为$r$,要把$(x,fa_x)$这条边删掉
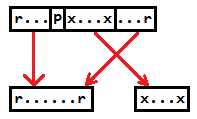
用平衡树维护序列,分割合并一下就好(显然图中$p=fa_x$)
为了找到以$x$为根的子树的位置,我们还要存$first_i$表示节点$i$第一次在欧拉序列中出现的位置,$last_i$表示节点$i$最后一次在欧拉序列中出现的位置(为了方便实现,存的都是平衡树中的节点编号)
在删边时因为丢弃了$p$,所以要判断$first_p$是否需要更新
数值操作就直接在平衡树上打标记就好了
据说ETT可以link可以cut可以换根,但是好像很困难的样子,改天去补一下(主要就是换根,换根解决了什么都解决了)
如果有兴趣可以参考这个题解的T3
p.s.第一次看到这么奇妙的强制在线法,居然是用交互的形式
#include<stdio.h>
#include<stdlib.h>
#define inf 2147483647
#define mod 99990001
#define ll long long
struct edge1{
int to,nex,v;
}e[400010];
struct edge2{
int a,b,v;
}ee[200010];
struct treap{
int l,r,fa,fix,siz,mp,bl,v,ad,mu;
treap(){
fix=rand();
siz=mu=1;
mp=inf;
}
}t[400010];
struct pair{
int l,r;
pair(){l=r=0;}
};
int h[200010],dep[200010],fav[200010],fir[200010],las[200010],M;
void add(int a,int b,int c){
M++;
e[M].to=b;
e[M].v=c;
e[M].nex=h[a];
h[a]=M;
}
int min(int a,int b){return a<b?a:b;}
void pushup(int x){
t[x].siz=t[t[x].l].siz+t[t[x].r].siz+1;
t[x].mp=min(t[x].bl,min(t[t[x].l].mp,t[t[x].r].mp));
}
void gao(int x,int a,int b){
t[x].v=(b+t[x].v*(ll)a)%mod;
t[x].ad=(b+t[x].ad*(ll)a)%mod;
t[x].mu=(t[x].mu*(ll)a)%mod;
}
void pushdown(int x){
if(t[x].mu!=1||t[x].ad!=0){
if(t[x].l)gao(t[x].l,t[x].mu,t[x].ad);
if(t[x].r)gao(t[x].r,t[x].mu,t[x].ad);
t[x].mu=1;
t[x].ad=0;
}
}
pair split(int x,int k){
pair s;
if(x==0)return s;
pushdown(x);
if(k<=t[t[x].l].siz){
s=split(t[x].l,k);
t[x].l=s.r;
if(s.r)t[s.r].fa=x;
s.r=x;
}else{
s=split(t[x].r,k-t[t[x].l].siz-1);
t[x].r=s.l;
if(s.l)t[s.l].fa=x;
s.l=x;
}
pushup(x);
return s;
}
int merge(int x,int y){
if(x==0)return y;
if(y==0)return x;
if(t[x].fix<t[y].fix){
pushdown(x);
t[x].r=merge(t[x].r,y);
t[t[x].r].fa=x;
pushup(x);
return x;
}else{
pushdown(y);
t[y].l=merge(x,t[y].l);
t[t[y].l].fa=y;
pushup(y);
return y;
}
}
int top(int x){
while(t[x].fa)x=t[x].fa;
return x;
}
int lt(int x){
int s=t[t[x].l].siz;
while(t[x].fa){
if(t[t[x].fa].r==x)s+=t[t[t[x].fa].l].siz+1;
x=t[x].fa;
}
return s;
}
int cut(int x){
int rt,L,R;
pair s,t1,t2;
rt=top(fir[x]);
L=lt(fir[x]);
R=lt(las[x]);
s=split(rt,L);
t1=split(s.l,L-1);
t2=split(s.r,R-L+1);
t[t2.l].fa=0;
if(fir[t[t1.r].bl]==t1.r){
for(x=t2.r;t[x].l;x=t[x].l);
fir[t[t1.r].bl]=x;
}
t[merge(t1.l,t2.r)].fa=0;
return t[t1.r].v;
}
void dfs(int f,int x){
for(int i=h[x];i;i=e[i].nex){
if(e[i].to!=f){
dep[e[i].to]=dep[x]+1;
fav[e[i].to]=e[i].v;
M++;
if(fir[x]==0)fir[x]=M;
t[M].v=e[i].v;
t[M].mp=t[M].bl=x;
dfs(x,e[i].to);
}
}
las[x]=++M;
if(fir[x]==0)fir[x]=M;
t[M].v=fav[x];
t[M].mp=t[M].bl=x;
}
int main(){
t[0].siz=0;
int n,i,a,b,c;
scanf("%d",&n);
for(i=1;i<n;i++){
scanf("%d%d%d",&ee[i].a,&ee[i].b,&ee[i].v);
add(ee[i].a,ee[i].b,ee[i].v);
add(ee[i].b,ee[i].a,ee[i].v);
}
M=0;
dfs(0,1);
for(i=1;i<M;i++)merge(top(i),i+1);
for(i=1;i<n;i++){
scanf("%d",&c);
a=ee[c].a;
b=ee[c].b;
c=cut(dep[a]>dep[b]?a:b);
printf("%d\n",c);
fflush(stdout);
a=top(fir[a]);
b=top(fir[b]);
if(t[a].siz<t[b].siz||(t[a].siz==t[b].siz&&t[a].mp<t[b].mp)){
gao(a,c,0);
gao(b,1,c);
}else{
gao(a,1,c);
gao(b,c,0);
}
}
}
