[py]函数中yield多次返回,延迟计算特性-杨辉三角

搞清什么是杨辉三角

每行是一个数组,

第一行: [1] 
第二行: [1, 1]
第三行: [1, 2, 2, 1]
...

画的好看点就是,不过没啥卵用

          1
         /         1   1
       / \ /       1   2   1
     / \ / \ /     1   3   3   1
   / \ / \ / \ /   1   4   6   4   1
 / \ / \ / \ / \ / 1   5   10  10  5   1

打印杨辉三角

首先要解决一个函数,多次返回值, 我们知道py函数返回多个值,没啥问题. 但是要多次返回值呢?需要借助生成器来完成, 生成器的好处是可以保留现场,延迟操作

套路是 函数里使用yield关键字,相当于return, 不过可以有多个yield,但是不可以有多个return.

yield可以返回一个generator类型的值, 可以for in遍历

那么可不可以手动创建一个yield值呢? 可以

方法: 将列表推导式(一股脑生成所有值,为了简化for代码)的方括号改成圆括号即可.

x = [x * x for x in range(10)]
g = (x * x for x in range(10)) #2种遍历方法: 法1: next(g) 需处理StopIteration异常,  法2: for i in g

>>> next(g)
0
>>> next(g)
1
>>> next(g)
4
>>> next(g)
...

生成器小结:

小结

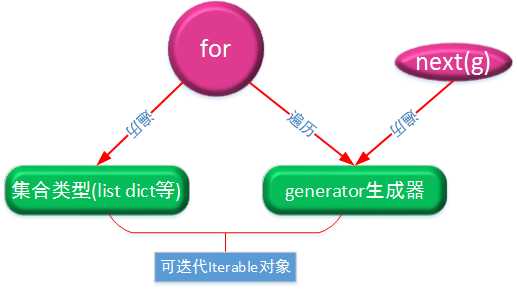
• 凡是可作用于for循环的对象都是Iterable类型；

• 凡是可作用于next()函数的对象都是Iterator类型，它们表示一个惰性计算的序列；

• 集合数据类型如list、dict、str等是Iterable但不是Iterator，不过可以通过iter()函数获得一个Iterator对象。

• Python的for循环本质上就是通过不断调用next()函数实现的，例如：

  for x in [1, 2, 3, 4, 5]:
  pass

  实际上完全等价于：

  # 首先获得Iterator对象:
  it = iter([1, 2, 3, 4, 5])
  # 循环:
  while True:
  try:
      # 获得下一个值:
      x = next(it)
  except StopIteration:
      # 遇到StopIteration就退出循环
      break

先搞清楚生成器-用在函数里,多次返回值,具有保留现场,延迟操作的功效

这个程序执行过程, for语句一股脑构造好arr数据后一次性返回

def sc(N):
    arr = []
    for i in range(N):
        arr.append(i**2)
    return arr

for i in sc(10):
    print(i)

改成yield(相当于return,所以一定写在函数里,但可以写多条.)
执行过程: 遇到yield即刻保留现场,yield的内容返回给调用者. 再次调用函数时,从上次yield下一条语句开始执行,遇到下一个yield直接返回内容.

def sc(N):
    for i in range(N):
        yield i ** 2

for i in sc(10):
    print(i)

如果还不太清楚,且看

yield返回的是generator

def odd():
    print('step 1')
    
g = odd()
print(type(odd)) #<class 'function'>
print(type(g))   #<class 'NoneType'>

def odd():
    print('step 1')
    yield (1)
    print('step 2')
    yield (2)
    print('step 3')
    yield (3)
    
g = odd()
print(type(odd))#<class 'function'>
print(type(g))  #<class 'generator'>

yield调用过程, 和调用的2种方法

def odd():
    print('step 1')
    yield (1)
    print('step 2')
    yield (2)
    print('step 3')
    yield (3)
    
g = odd()
print(type(g))
print(type(odd))


#遍历生成器,方法1: 最后没值了后异常(StopIteration)
next(g)
next(g)
next(g)


#遍历生成器,方法2: 不用关心StopIteration异常
for i in g:
    print(g)

---
step 1
1
step 2
2
step 3
3

打印杨辉三角

# 期待输出:

# [1]
# [1, 1]
# [1, 2, 2, 1]
# [1, 3, 3, 1]
# [1, 4, 6, 4, 1]
# [1, 5, 10, 10, 5, 1]
# [1, 6, 15, 20, 15, 6, 1]
# [1, 7, 21, 35, 35, 21, 7, 1]
# [1, 8, 28, 56, 70, 56, 28, 8, 1]
# [1, 9, 36, 84, 126, 126, 84, 36, 9, 1]



- 首先构造这样的数列
#第1次返回[1]
#第2次返回[1, 1]
#第3次返回[1, 2, 1]
# 每行的模式
[1, 2, 2, 1] = [1,2]+[2,1]

for i in range(n):
    i=i+1
    arr = list(range(1, i))
    arr = arr + list(reversed(arr))

- 其次yield实现多次返回

def yanghui():
    yield [1]
    yield [1, 1]
    yield [1, 2, 2, 1]


for i in yanghui():
    print(i)

---
[1]
[1, 1]
[1, 2, 2, 1]

最终实现

def yanghui(n):
    for i in range(n):
        #
        i=i+1
        arr = list(range(1, i))
        arr = arr + list(reversed(arr))
        # list(range(1, 1)) ==> []
        if arr == []:
            arr = [1]
        yield arr


for i in yanghui(10):
    print(i)