一、前述
逻辑回归是一种分类算法,对多元线性回归的结果做一定的缩放。是一种线性(x是一次的)有监督(有x,y)分类(要么是正列,要么是负例)算法。
二、具体
如果最后预测的结果大于0.5 是正例 小于0.5是负例
做分类的误差来源于两种情况:
假设Y是正列 1-p^
假如本来是1这个类别:预测出来的结果是0.6则预测对了预测的误差是1-0.6=0.4
假如本来是1这个类别:预测出来的结果是0.1 则误差1-0.1=0.9
假设是负例p^
假设预测出来的是0.1 则误差是0.1
假设预测出来的是0.6 则误差是0.6
三、代码
#逻辑回归预测鸢尾花,根据花瓣的宽度 import numpy as np from sklearn import datasets from sklearn.linear_model import LogisticRegression import matplotlib.pyplot as plt iris = datasets.load_iris()# 鸢尾花数据集 print(list(iris.keys())) print(iris[‘DESCR‘])#数据集的描述 print(iris[‘feature_names‘])#数据集的特证名字 #150条数据 三种花 每种花50条数据 #根据花的花瓣,花萼,花蕊来分类 X = iris[‘data‘][:, 3:] # 逗号左边第一行到所有行 ,逗号右边第3列开始到最后 总共4列 实际上就是最后一列 # print(X) print(iris[‘target‘]) y = (iris[‘target‘] == 2).astype(np.int) print(y) #保留类别为2的花。 log_reg = LogisticRegression()#构建逻辑回归 log_reg.fit(X, y)#根据最后一个花瓣的宽度来预测 X_new = np.linspace(0, 3, 1000).reshape(-1, 1)#0-3之间切分1000次 print(X_new) y_proba = log_reg.predict_proba(X_new)#预测的概率 给一个0-1之间的一个概率值 y_hat = log_reg.predict(X_new)#预测的结果 print(y_proba) print(y_hat) plt.plot(X_new, y_proba[:, -1], ‘g-‘, label=‘Iris-Virginica‘) plt.plot(X_new, y_proba[:, 0], ‘b--‘, label=‘Not Iris-Virginica‘) plt.show() print(log_reg.predict([[1.7], [1.5]])) #PS 对应1.6的时候正列结果是鸢尾花 #小于1.6的时候是负例不是鸢尾花
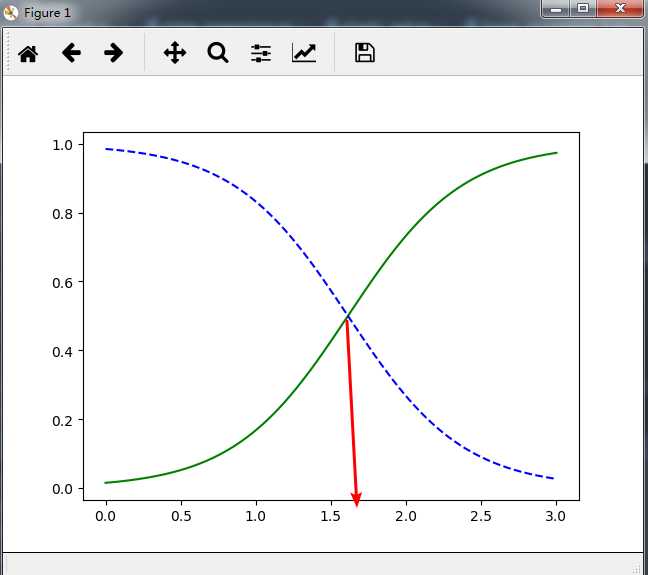
PS:1.6是正负例的交界。
