定义：

　　Treap,顾名思义，就是tree和heap的结合，既满足二叉搜索树的性质，又满足二叉堆的性质
　　但是一个要求节点值小于右儿子的值,一个要求节点值大于右儿子的值,显然不可能做到
　　那我们只能一个节点存两个值,一个满足二叉搜索树性质,一个满足二叉堆的性质:如下图

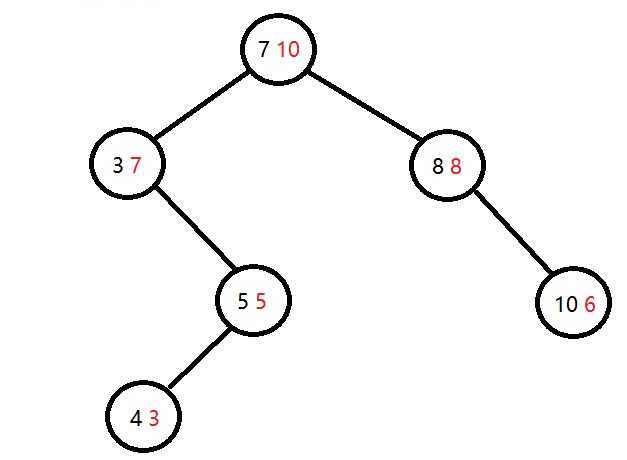
　　节点中黑色的值满足二叉搜索树的性质，红色的值满足二叉(大根)堆的性质。并且给定这些节点,这棵Treap是唯一的

用处：

　　那这个Treap到底有什么用呢?
　　我们知道二叉搜索树可以维护一个有序的序列期望插入删除期望复杂度O(logn)
　　但是如果是极限数据的话,二叉搜索树可能会退化成链表,复杂度变为O(n),相当于白用了
　　于是我们为了防止它退化成链表,就让每个节点维护两个数,使另一个数满足二叉堆的性质
　　使他可以自己平衡,成为平衡树,这就是Treap

具体操作

　　存储：

struct Treap{
	int key,prio,size,num;//key满足二叉搜索树,prio满足二叉堆,num是key值的数目,size是子树中num之和 
	Treap* son[2];
	Treap(){
		memset(this,0,sizeof(Treap));
	}
	Treap(int k){
		key=k,prio=random(),size=num=1,son[0]=son[1]=0;
	}
}*root;

struct Treap{
    int key,prio,size,num;//key满足二叉搜索树,prio满足二叉堆,num是key值的数目,size是子树中num之和 
    Treap* son[2];
    Treap(){
        memset(this,0,sizeof(Treap));
    }
    Treap(int k){
        key=k,prio=random(),size=num=1,son[0]=son[1]=0;
    }
}*root;

　　插入：

　　　　我们对于每个要插入的数据配上一个随机生成的数，按照二叉搜索树的插入方法插入到树中
　　　　但是这就可能使Treap不满足二叉堆的性质了。如再上图中插入就成了下面这样

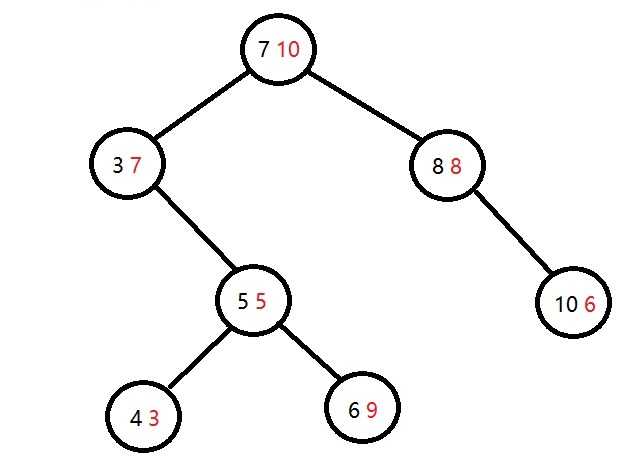
　　　　然后就是平衡树的精髓所在了——旋转