问题描述：
假设存在n个签，通过抽取四次，如果四次抽取的和为m即胜利。
初始解：
1 for(int a = 0; a < n; a++) 2 { 3 for(int b = 0; b < n; b++) 4 { 5 for(int c = 0; c < n; c++) 6 { 7 for(int d = 0; d < n; d++) 8 { 9 if(k[a] + k[b] + k[c] + k[d] == m) 10 f = true; 11 } 12 } 13 } 14 }
难度增加，将n的限制条件为1~1000，此时，四重循环明显复杂度过高，需改进算法。
上面所记载的程序的循环部分。最内侧关于d的循环所做的事就是
检查是否有d使得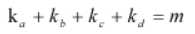
通过对式子移项，就能得到另一种表达式
检查是否有d使得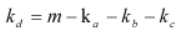
就是说，检查数组k中所有元素，判断是否有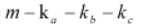
结合二分搜索进行求解，注意二分搜索前提为该数组排好序（可用c++自带的binary_serach）
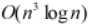
1 int n, m, k[MAX_N]; 2 3 bool binary_serach(int x) 4 { 5 int l = 0, r = n; 6 while(r - 1 >= 1) 7 { 8 int i = (l + r) / 2; 9 if(k[i] == x) 10 return true; 11 else if(k[i] < x) 12 l = i + 1; 13 else 14 r = i; 15 } 16 return false; 17 } 18 19 void solve() 20 { 21 sort(k, k + n); 22 bool f = false; 23 for(int a = 0; a < n; a++) 24 { 25 for(int b = 0; b < n; b++) 26 { 27 for(int c = 0; c < n; c++) 28 { 29 if(binary_serach(m - k[a] - k[b] - k[c])) 30 { 31 f = true; 32 } 33 } 34 } 35 } 36 if(f) 37 cout << "Yes" << endl; 38 else 39 cout << "No" << endl; 40 }
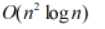的算法
着眼于内层的两个循环
检查是否有c和d使得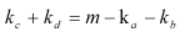
这种情况并不能直接使用二分搜索。但是，如果预先枚举出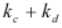
所得的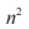
个数字并排好序，便可以利用二分搜索了。
1 int n, m, k[MAX_N]; 2 int kk[MAX_N * MAX_N]; 3 bool binary_serach(int x) 4 { 5 int l = 0, r = n * n; 6 while(r - 1 >= 1) 7 { 8 int i = (l + r) / 2; 9 if(kk[i] == x) 10 return true; 11 else if(kk[i] < x) 12 l = i + 1; 13 else 14 r = i; 15 } 16 return false; 17 } 18 19 void solve() 20 { 21 for(int c = 0; c < n; c++) 22 { 23 for(int d = 0; d < n; d++) 24 { 25 kk[c * n + d] = k[c] + k[d]; 26 } 27 } 28 29 sort(kk, kk + n * n); 30 for(int a = 0; a < n; a++) 31 { 32 for(int b = 0; b < n; b++) 33 { 34 if(binary_serach(m - k[a] - k[b])) 35 { 36 f = true; 37 } 38 } 39 } 40 if(f) 41 cout << "Yes" << endl; 42 else 43 cout << "No" << endl; 44 }
