第五章 投资项目资本预算

[TOC]

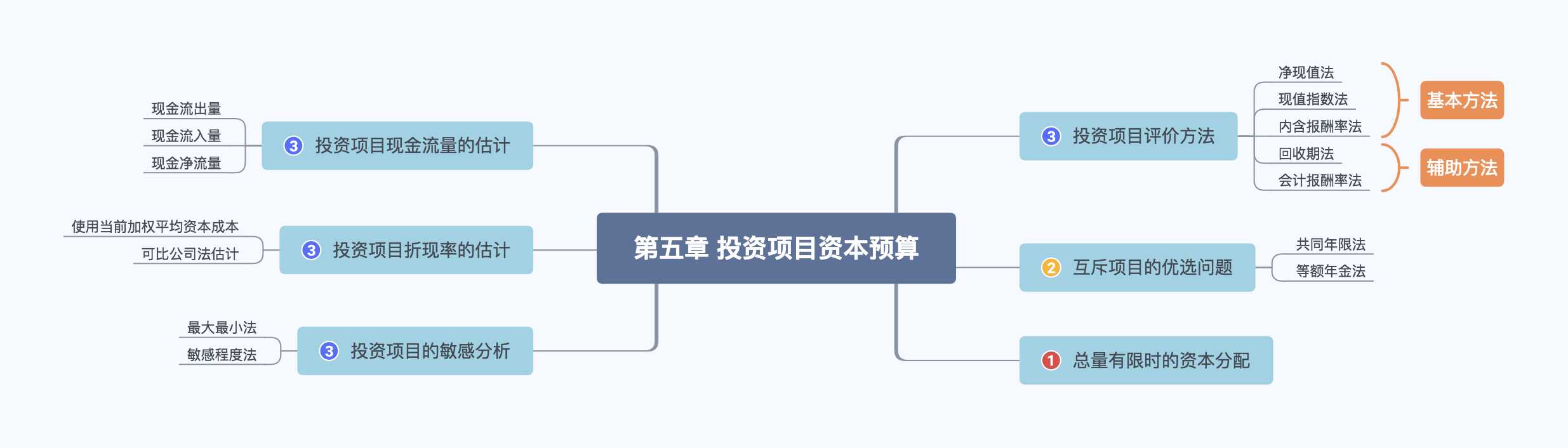
投资项目评价方法 ★★★

净现值法(NPV)

现值指数(PI)

\(现值指数 = \frac{现金流入量现值}{现金流出量现值}\)

现值指数>1，净现值>0；

现值指数=1，净现值=0；

现值指数<1，净现值<0；

消除投资额差异，未消除项目期限影响

内含报酬率(IRR)

未来现金流入量等于未来现金流出量时的折现率，NPV=0

IRR>项目资本成本，NPV>0，可行

IRR=项目资本成本，NPV=0，没必要采纳

IRR<项目资本成本，NPV<0，放弃

回收期法

1. 静态回收期-不考虑时间价值
   1. \(回收期 = \frac{初始投资}{每年现金金流入量}\)
   2. \(回收期 = 累计现金流量出现正数年份 - 1 + \frac{上一年未收回投资}{当年现金流入量}\)
2. 动态回收期-考虑时间价值
   1. \(回收期 = 累计现金流量现值出现正数年份 - 1 + \frac{上一年未收回投资现值}{当年现金流入量现值}\)

会计报酬率法

\(会计报酬率 = \frac{年均净收益}{原始投资额}\)

年均净收益按照经营期计算，不包括建设期

互斥项目的优选问题 ★★

1. 项目寿命期相同，投资额不同，净现值法优先，选择NPV较大的
2. 项目寿命期不相同，采用共同年限或等额年金法，选择永续净现值较大的

共同年限法

年限最小公倍数，重置

等额年金法

1. 计算两个项目的净现值
2. 计算净现值的等额年金
3. 计算项目的永续现值

总量有限的资本分配 ★

1. 按照现值指数排序
2. 按总量选择投资组合NPV最高的

投资项目现金流量的估计 ★★★

现金流量清单

1. 初始阶段现金流量
   1. 新购置固定资产的支出【-】
   2. 额外资本支出（运输费、安装费、调试费、加盟费等）【-】
   3. 占用原有资产（如原有的土地、厂房、设备和原材料等）
      1. 占用原有资产的变现价值【-】
      2. 丧失的变现损失抵税（变现价值小于账面价值）【-】
      3. 丧失的变现收益纳税（变现机制大于账面价值）【+】
   4. 营运资本需要（投入或垫支）
      1. 营运资本需要 = 经营流动资产增加 - 经营流动负债增加
      2. 营运资本占销售百分比
      3. 年初追加投入营运资本金额【-】
2. 经营期间现金流量
   1. 新产品（业务）税后营业收入【+】
   2. 占用原有资产每年丧失的税后租金收入【-】
   3. 新产品（业务）对原有产品（业务）收入的影响
      1. 竞争关系：减少原有产品税后收入【-】
      2. 互补关系：增加原有产品税后收入【+】
   4. 新产品（业务）税后付现成本【-】
   5. 新产品（业务）对原有产品（业务）付现成本的影响
      1. 竞争关系：减少原有产品的税后付现成本【+】
      2. 互补关系：增加原有产品的税后付现成本【-】
   6. 按税法计算的年折旧（摊销）抵税【+】

   直接法：营业现金流量 = 营业收入 - 付现成本 - 所得税（\(EBIT \times T\)）

   \(营业现金流量 = 营业收入 - （营业成本 - 折旧摊销） - EBIT \times T\)

   \(营业现金流量 = EBIT - EBIT \times T + 折旧摊销\)

   间接法：\(营业现金流量 = EBIT \times (1 - T) + 折旧摊销\)

   \(营业现金流量 = （营业收入 - 付现成本 -折旧摊销）\times （1-T）+ 折旧摊销\)

   分项计算法：\(营业现金流量 = 营业收入 \times （1-T）- 付现成本 \times （1-T）+ 折旧摊销 \times T\)

3. 项目处置时现金流量
   1. 项目结束时垫支的营运资本收回【+】
   2. 处置或出售资产的变现价值【+】
      1. 提前变现 账面价值>税法残值
      2. 正常使用终结 账面价值=税法残值
      3. 延期使用 账面价值=税法残值
   3. 变现净收益（净损失）影响所得税
      1. 变现收益纳税【-】
      2. 变现损失抵税【+】

固定资产更新决策

1. 平均年成本法-未来使用年限不同： \(\frac{未来使用年限内现金流出总现值}{普通年金现值系数}\)
2. 总成本法-未来使用年限相同： \(未来使用年限内现金流出量的总现值\)
3. 差额分析法-未来使用年限形同：\(差额现金流的净现值\)

固定资产经济寿命

\(平均年成本 = \frac{原值 - 折余价值现值 + 运行成本现值}{年金现值系数 }\)

投资项目折现率的估计 ★★★

同类产品的扩建项目（经营风险一致）

1. 确定公司当前的\(\beta_{资产}\)
   1. 卸载杠杆：\(\beta_{资产} = \frac{公司当前的\beta_{权益}} {1 + 公司目前的产权比率 \times （1-所得税税率）}\)
2. 确定公司新项目的\(\beta_{权益}\)
   1. \(\beta_{权益} = \beta_{资产} \times [1 + 公司目标的产权比率 \times （1-所得税税率）]\)
3. 根据资本资产定价模型确定股权资本成本
   1. \(股权资本成本 = R_{f} + \beta_{权益} \times (R_m - R_f)\)
4. 确定债务税前和税后资本成本
   1. 到期收益率法
   2. 风险调整法
   3. 发行日贴现法
5. 确定加权平均资本成本
   1. \(加权平均资本成本 = 债务税后资本成本 \times 债务目标比重 + 股权资本成本 \times 股权目标比重\)

非同类产品的扩建项目（经营风险不一致，财务风险不一致）

1. 将可比公司的\(\beta_{权益}\)转换为\(\beta_{资产}\)
   1. $\beta_{资产} = \frac{\beta_{权益}}{1+可比公司产权比率 \times（1-可比公司所得税税率）} $
2. 将\(\beta_{资产}\)转换为目标公司\(\beta_{权益}\)
   1. \(\beta_{权益} = \beta_{资产} \times [1+目标公司产权比率 \times （1-目标公司所得税税率）]\)
3. 根据资本资产定价模型计算目标公司的股权资本成本
   1. \(股权资本成本 = R_{f} + \beta_{权益} \times (R_m - R_f)\)
4. 确定债务税前和税后资本成本
   1. 到期收益率法
   2. 风险调整法
   3. 发行日贴现法
5. 确定加权平均资本成本
   1. \(加权平均资本成本 = 债务税后资本成本 \times 债务目标比重 + 股权资本成本 \times 股权目标比重\)

权益β与资产β

1. \(\because V = D + E\)

   V:企业价值

   D:负债价值

   E:权益价值

2. \(\therefore \beta = \beta_{负债} \times \frac{D}{V} + \beta_{权益} \times \frac{E}{V}\)

3. \(\because V = V_U + D\times T_C\)

   有税MM理论

   \(V_U\):无负债企业价值

   \(D\times T_C\):利息抵税现值

4. \(\therefore \beta = \beta_{负债} \times \frac{D\times T_C}{V} + \beta_{U} \times \frac{V_U}{V}\)

   \(\beta_U\):无负债β值，即\(\beta_{资产}\)

5. \(\therefore D + E = V_U + D\times T_C\)
6. \(\therefore \beta_{负债} \times \frac{D}{V} + \beta_{权益} \times \frac{E}{V} = \beta_{负债} \times \frac{D\times T_C}{V} + \beta_{U} \times \frac{V_U}{V}\)
7. 根据5， \(\therefore V_U = D + E - D\times T_C = E + D \times (1- T_C)\)

8. 根据6和7，且\(\beta_{负债} = 0\)（债务系统风险忽略），\(\therefore \beta_{权益} = \beta_{资产} \times [1 + \frac{D \times (1-T)}{E}]\)

投资项目的敏感性分析 ★★★

敏感性分析概念

单因素分析

敏感性分析方法

最大最小法应用步骤

1. 给定计算净现值的每个变量最可能发生的预期值【原始投资、销售量、单价、单位变动成本】
2. 根据变量的预期值计算基准净现值
3. 选择一个变量并假设其他变量不变，令净现值为零，计算选定变量的临界值【\(原始投资_{上限}\)、\(销售量_{下限}\)、\(单价_{下限}\)、\(单位变动成本_{上限}\)】

敏感程度法应用步骤

1. 计算项目基准净现值
2. 假设某一变量发生一定幅度的变化，而其他因素不变情况下，重新计算净现值
3. 计算选定变量的敏感系数:\(敏感系数 = \frac{目标值变动百分比}{选定变量变动百分比}\)

敏感系数大于0，正相关

敏感系数小于0，负相关

敏感系数等于0，不相关

思维导图