作为二叉排序树,红黑树具有如下5个性质:
1 所有结点的颜色是红色或者黑色。
2 根结点是黑色。
3 所有的叶子结点(包含NULL)是黑色。
4 每个红色的结点的孩子结点必须是黑色。
5 从任意结点出发,到其所有叶子结点的简单路径上都包含相同数量的黑色结点。
它确保没有一条路径会比其他路径长1倍。因此,红黑树是相对接近平衡的二叉树,时间复杂度是O(log2n)。
当前结点是红色,删除时根据当前结点进行调整。调整时红色上移,黑色下移,以改变颜色的最高点作为支点进行旋转,旋转方向与红色移动方向相同。每次旋转都需要更新根结点。
注:三角形表示子树,x是当前结点即当前结点或删除后当前结点,xp是父结点,xpp是爷爷结点,xppr是爷爷结点的右孩子。
插入的5种情况(省略示意图的对称情况,下同)如下:
1 父结点为空
当前结点设为黑色并作为根结点返回。
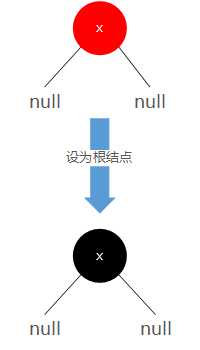
2 父结点为黑色
当前结点设为父结点的孩子结点,父结点设为当前结点的父结点。
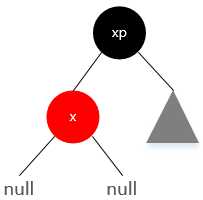
3 父结点为红色
3.1 父结点的兄弟结点存在且为红色(父结点是爷爷结点的左孩子)
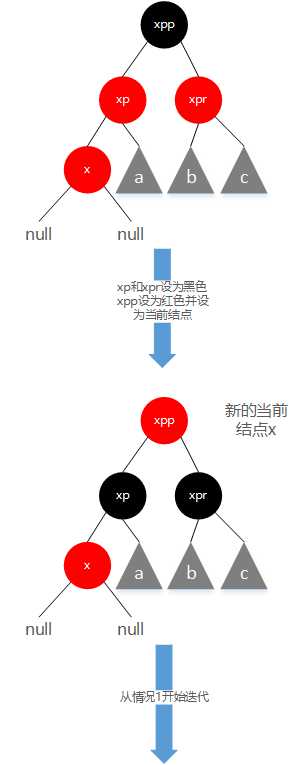
3.2 当前结点是父结点的左孩子
3.3 当前结点是父结点的右孩子
删除的8种情况如下:
1 当前结点为空或根结点
不需要调整。
2 当前结点的父结点为空
把当前结点设为黑色并作为根结点返回。
3 当前结点是红色
把当前结点设为黑色。
4 当前结点(黑色—隐藏的默认条件)是父结点的左孩子
4.1 父结点的右孩子存在并且为红色
4.2 不存在兄弟结点
父结点设为当前结点,并从第1种情况开始迭代。
4.3 兄弟结点的左右孩子都为黑色(空结点为黑色)
4.4 兄弟结点的孩子结点中至少有一个是红色
4.4.1 兄弟结点的右孩子为黑色
4.4.2 兄弟结点的右孩子为红色
参考资料
