题目链接 Power Tower
题意 给定一个序列,每次给定$l, r$
求$w_{l}^{w_{l+1}^{w_{l+2}^{...^{w_{r}}}}}$ 对m取模的值
根据这个公式
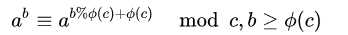
每次递归计算。
因为欧拉函数不断迭代,下降到$1$的级别大概是$log(m)$的,那么对于每一次询问最多需要递归$log(m)$次
注意每次求解欧拉函数的时候要用map存下来,方便以后查询
#include <bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for (int i(a); i <= (b); ++i)
#define dec(i, a, b) for (int i(a); i >= (b); --i)
typedef long long LL;
const int N = 1e5 + 10;
int n, q;
LL a[N];
LL m;
map <LL, LL> f;
LL phi(LL n){
if (f.count(n)) return f[n];
LL ans = n, z = n;
for (LL i = 2; i * i <= n; ++i){
if (n % i == 0){
ans -= ans / i;
while (n % i == 0) n /= i;
}
}
if (n > 1) ans -= ans / n;
return f[z] = ans;
}
LL Pow(LL a, LL b, LL mod){
LL ret = 1;
LL fl = a >= mod;
for (; b; b >>= 1){
if (b & 1){
ret *= a;
if (ret >= mod) fl = 1, ret %= mod;
}
a *= a;
if (a >= mod) a %= mod, fl = 1;
}
return ret + fl * mod;
}
LL solve(int l, int r, LL mod){
if (l == r) return a[l];
if (mod == 1) return 1;
return Pow(a[l], solve(l + 1, r, phi(mod)), mod);
}
int main(){
scanf("%d%lld", &n, &m);
rep(i, 1, n) scanf("%lld", a + i);
scanf("%d", &q);
while (q--){
int x, y;
scanf("%d%d", &x, &y);
printf("%lld\n", solve(x, y, m) % m);
}
return 0;
}
