与队列和堆栈一样,树也是人为构造的一种数据存储逻辑。
树,一般是为了使数据的搜索更加容易而构筑的,比如下文会提到的二叉搜索树。
首先我们来看一下树的课本定义。
树(Tree),是元素的集合。
假设我们有这样一组数据,{ 6,3,5,1,8,7,9 },我们使用树的形式来存放他们,得到了这样一棵树。
(在一棵有实际意义的树中,节点之间其实是有一定关联的。我们在这里仅仅将数据随意存放,来展示一下树的概念。)
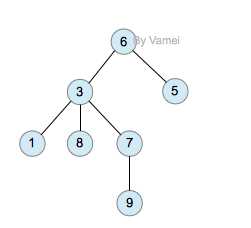
图-一棵仅用作示例,没有什么实际意义和用途的树
树有多个节点(node),用来存储元素。图中的每个数字所在的圆形就是一个节点。
每个节点之间用一根线相连,这些线,称为边(edge)。在一条边连接的两个节点中,靠近上层的节点称为父节点(parent),处在下层的节点称为子节点(children)。而处在最顶层,没有父节点的节点被称为根节点(root);没有子节点的节点称为叶节点(leaf)。同一个父节点下的同一层级的子节点相互称为兄弟节点(sibling)。很显然,这个图中的“6”就是根节点,也是“3”“5”的父节点。“5”是一个叶节点,也是“6”的子节点。“3”是“6”的子节点,但同时也是“1”“8”“7”的父节点。“1”“8”都是“3”的子节点,同事他们也是叶节点。“7”是“3”的子节点,是“9”的父节点。“9”是“7”的子节点,也是一个叶节点。“1”“8”“7”互为兄弟节点,“3”“5”互为兄弟节点。
树的层次被称为深度(depth)。可以看出上图中,“6”位于第一层,“3”和“5”位于第二层,“1”“8”“7”位于第三层,“9”位于第四层。这一棵树的深度是4。
然后我们再看一下树的课本定义:
1. 树是元素的集合。
2. 该集合可以为空。这时树中没有元素,我们称树为空树 (empty tree)。
3. 如果该集合不为空,那么该集合有一个根节点,以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。
*这里的第三点使用了递归的思想来定义一棵树。
树的实现
以C语言为例,当我们要实现一棵树的构造时,我们往往需要构造一种结构体来作为节点。但是一个父节点下的子节点个数是不同的,可能它有很多歌子节点,也可能它只有一个子节点。如果我们在结构体中,定义了多个子节点指针的变量,会造成内存的浪费。于是我们有了以下这种经典的实现方式(依然以上文那棵只有展示意义的树为例):
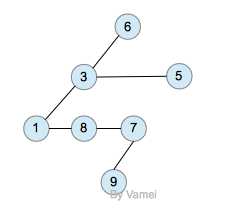
图-树的一种经典内存实现方式
在这种实现方式中,一个节点有两个指针,一个指向它的第一个子节点,一个指向它的下一个兄弟节点。这样,我们依然可以从根节点开始,遍历整棵树。
当然在实际操作中,为了方便,我们也可以让节点中增加一个指针去指向他的父节点。
二叉树
二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点。
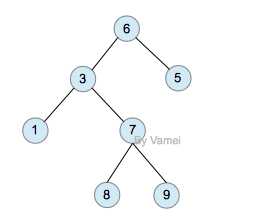
图-二叉树的结构示意/实现逻辑(这棵树依然只有展示意义)
因为子节点的个数确定了,所以每一个节点只需要两个指针,一个指向当前节点的左子节点(left children),一个指向右子节点(right children)。
二叉搜索树
在了解了树的定义和构造之后,我们可以看看树的实际应用了。
前文出现的树都只作为展示示例,而并没有什么实际意义。
现在,我们考虑为二叉树的数据存放增加一个条件:每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大。
所谓左子树,就是把它的左子节点视为一个根节点之后,这个根节点下的树。右子树同理。
增加了上述这个条件后,我们就得到了 二叉搜索树。
我们对{ 6,3,5,1,8,7,9 }这组数据构造一个二叉搜索树:(构造方式只要满足条件就可以,并不是唯一的)。
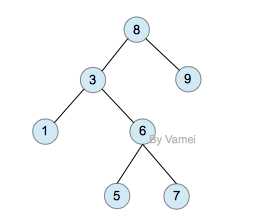
图-二叉搜索树
构造了这样的结构之后,我们可以更快的对数据进行搜索。我们按照以下逻辑对数据x进行查找:
1. 如果x等于根节点,那么找到x,停止搜索 (终止条件)
2. 如果x小于根节点,那么搜索左子树,回到第一步
3. 如果x大于根节点,那么搜索右子树,回到第一步
我们在进行搜索时,对二叉搜索树进行操作的最大次数就是这棵树的深度。
*在使用C语言构造搜索二叉树的过程中,你可能会发现“删除”操作异常麻烦。有一种简单的替代操作,称为懒惰删除(lazy deletion)。在懒惰删除时,我们并不真正从二叉搜索树中删除该节点,而是将该节点标记为“已删除”。这样,我们只用找到元素并标记,就可以完成删除元素了。如果有相同的元素重新插入,我们可以将该节点找到,并取消删除标记。。树所占据的内存空间不会因为删除节点而减小。懒惰节点实际上是用内存空间换取操作的简便性。
