矩阵快速幂讲解
若求斐波那契数列第n项的数值,我们可以递推求得,若n值(>1e10)很大,我们一个一个求,一定会超时,下面讲解一下用矩阵快速幂求解
矩阵快速幂就是:求矩阵A^n的矩阵,如同快速幂一样,代码极其相似,将快速幂中的整数乘法改为矩阵的乘法即可
矩阵乘法: 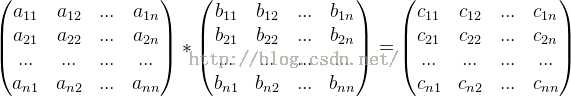
其中c[i][j]为矩阵A的第i行与矩阵B的第j列对应想乘的和,即
矩阵乘法代码实现如下:

Matrix multiplicative(Matrix a,Matrix b){ Matrix res; memset(res.matrix,0,sizeof(res.matrix)); for(int i = 0 ; i < n ; i++) for(int j = 0 ; j < n ; j++) for(int k = 0 ; k < n ; k++) res.matrix[i][j] += a.matrix[i][k]*b.matrix[k][j]; return res; }
矩阵快速幂代码如下:

Matrix pow(Matrix mx,int m){ Matrix res,base=mx; init(res); //初始为单位矩阵,即除主对角线都是1外,其他都是0 while(m) { if(m&1) res=multiplicative(res,base); base=multiplicative(base,base); m>>=1; } return res; }
斐波那契数列递推式为F(n)=F(n-1)+F(n-2) (n>=2)
F(0)=0,F(1)=1
根据递推式我们可以列出两个方程:F(n)=F(n-1)+F(n-2)和F(n-1)=F(n-2)+F(n-3)
由此
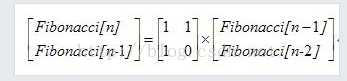
即
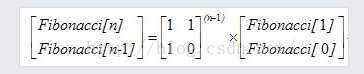
代码如下:

#include<stdio.h> #include<cstring> #define LL long long #define M 10 #define MOD 1000000007 struct Matrix{ LL matrix[M][M]; }; int n;//矩阵的阶数 void init(Matrix &res){ for(int i=0;i<=n;i++) { for(int j=0;j<=n;j++) res.matrix[i][j]=0; res.matrix[i][i]=1; } } Matrix multiplicative(Matrix a,Matrix b){ Matrix res; memset(res.matrix,0,sizeof(res.matrix)); for(int i = 0 ; i < n ; i++) for(int j = 0 ; j < n ; j++) for(int k = 0 ; k < n ; k++) res.matrix[i][j] =(res.matrix[i][j]%MOD+a.matrix[i][k]%MOD*b.matrix[k][j]%MOD)%MOD; return res; } Matrix pow(Matrix mx,int m){ Matrix res,base=mx; init(res); //初始为单位矩阵,即除主对角线都是1外,其他都是0 while(m) { if(m&1) res=multiplicative(res,base); base=multiplicative(base,base); m>>=1; } return res; } int main(){ int m; n=2; scanf("%d",&m); Matrix base,res; base.matrix[0][0]=base.matrix[0][1]=base.matrix[1][0]=1; base.matrix[1][1]=0; res=pow(base,m-1); if(m==0) puts("0"); else if(m==1) puts("1"); else printf("%lld\n",res.matrix[0][0]%MOD); return 0; }
常见递推类型:


