机器学习-有监督-SVM

2018.1.16
给定训练集\(T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)}\)，一共有N个样本点。

一、线性可分的支持向量机

假定训练集是线性可分的。学习的目标是在特征空间找到一个分离超平面\(wx+b=0\)，能够将所有的样本正确划分为两类。学习的策略是间隔最大化。

1 目标函数

样本点\((x_i,y_i)\)到超平面\(wx+b=0\)的距离是
\[ d= \frac{|wx_i+b|}{\|w\|} \]
正例样本的\(y_i=+1\)，负例样本的\(y_i=-1\)，这样表示距离可以把绝对值符号去掉：
\[ d= \frac{y_i(wx_i+b)}{\|w\|} \]
\(y_i(wx_i+b)\)称为点\((x_i,y_i)\)到超平面\(wx+b=0\)的函数间隔。
所有样本点中离分离超平面最近的那个样本点的距离是：
\[ \min \limits_{i} {\frac{y_i(wx_i+b)}{\|w\|}} \]
在所有超平面中能让这个最小距离最大的那个w,b就是我们要的结果：
\[ \max \limits_{w,b} \min \limits_i {\frac{y_i(wx_i+b)}{\|w\|}} \]
为了方便求解，做如下变换：
对于\(\min \limits_{i} {\frac{y_i(wx_i+b)}{\|w\|}}\)这部分，假设点\((x_m,y_m)\)取得最小距离为\(d_0\)，也就是\(d_0 = {\frac{y_m(wx_m+b)}{\|w\|}}\)，对分子分母同时乘以或除以一个数，使得分子=1，也就是函数间隔=1，这时分母也发生了相应变化，因为\(w\)表示超平面wx+b=0的法向量方向，按比例缩放后方向没有变化，我们将变化后的分母还记作\(\|w\|\)。通过令最小函数间隔=1，目标函数变为：
\[ \begin{aligned} &\max \limits_{w,b} {\frac{1}{\|w\|}}\s.t. \qquad & {y_i(wx_i+b)}\geq 1,\quad i=1,2,\cdots,N \end{aligned} \]
约束条件保证了所有点都能分类正确。
为方便求解，进一步变化为：
\[ \begin{aligned} &\min \limits_{w,b} \frac{1}{2}\|w\|^2\\ s.t. \qquad &{y_i(wx_i+b)} \geq 1, \quad i=1,2,\cdots,N \end{aligned} \]

2 拉格朗日乘子法求解

2.1 构造拉格朗日函数：
\[ L(w,b,\alpha)= \frac{1}{2}\|w\|^2-\sum_{i=1}^{N}\alpha_i[y_i(wx_i+b)-1] \]
其中\(\alpha = (\alpha_1,\alpha_2,\cdots,\alpha_N)^T\)是拉格朗日乘子，\(\alpha_i \geq 0\)
2.2 把w,b看作常数，构造一个函数 \(\theta\)定义为 \(L(w,b,\alpha)\) 关于 \(\alpha\) 求最大值
\[ \theta = \max \limits_{\alpha} L(w,b,\alpha) \]
因为 \(\alpha_i \geq 0\) 且 \({y_i(wx_i+b)} \geq 1\)，所以
\[ \theta = \max \limits_{\alpha} L(w,b,\alpha) = \frac{1}{2}\|w\|^2 \]
2.3 原始问题 \(\min \limits_{w,b} \frac{1}{2}\|w\|^2\)等价于 $ \min \limits_{w,b} \max \limits_{\alpha} L(w,b,\alpha) \quad$。
根据拉格朗日对偶性，问题可变为 \(\max \limits_{\alpha} \min \limits_{w,b} L(w,b,\alpha)\)

(1) 求\(\min \limits_{w,b} L(w,b,\alpha)\)
\(\qquad\)对w,b分别求偏导数：
\[ \begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{N}\alpha_i y_i x_i \\frac{\partial L}{\partial b} &= -\sum_{i=1}^{N}\alpha_i y_i \end{aligned} \]
\(\qquad\)令偏导数=0得到：
\[ \begin{aligned} &w = \sum_{i=1}^{N}\alpha_i y_i x_i \& \sum_{i=1}^{N}\alpha_i y_i = 0 \end{aligned} \]
\(\qquad\)将这两个式子带回拉格朗日函数\(L(w,b,\alpha)\)得到：
\[ L(w,b,\alpha)= -\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) + \sum_{i=1}^{N} \alpha_i \]

(2) 求 \(\min \limits_{w,b} L(w,b,\alpha)\) 对\(\alpha\)的极大，$\max \limits_{\alpha} { {-\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) + \sum_{i=1}^{N} \alpha_i} } $ ,加负号得到：
\[ \begin{aligned} \min \limits_{\alpha} & {\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^{N} \alpha_i} \s.t. \qquad & \sum_{i=1}^{N} {\alpha_i y_i}=0\&\alpha_i \geq 0, i=1,2,\cdots, N \end{aligned} \]

(3) 假设求出了(2)中 $\alpha $ 的最优解 \(\alpha^* =(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*)^T\)
\(w\)的解为\(w^*=\sum_{i=1}^{N} \alpha_i^* y_i x_i\)
选择\(\alpha_i^*\)的一个正分量\(\alpha_i^*>0\),b的解为 \(b*=y_j -w^*x_j=y_j - \sum \alpha_i^* y_i (x_i x_j)\)

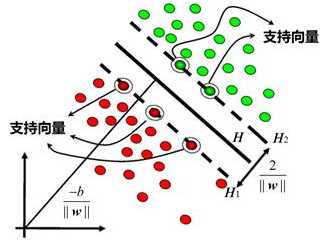
3 支持向量物理意义

在线性可分情况下，训练集的样本点中与分离超平面距离最近的样本点称为支持向量，即使得等式成立的样本点：\(y_i(wx_i+b)-1=0\).对正例点，支持向量在超平面\(H1:wx_i+b=1\)；对负例点，支持向量在超平面\(H2:wx_i+b=-1\).支持向量就是落在超平面H1和H2上的点。H1和H2称为间隔边界。间隔带的宽度是\(\frac{2}{\|w\|}\)。联系目标函数最小化\(\|w\|\)也就是要间隔最宽。 支持向量决定了模型，移动支持向量以外的样本点不影响结果，所以SVM实际上只用到了少数的样本点。但距离超平面最近的点刚好是噪声点，那么模型就会有问题。

二、线性不可分的支持向量机

1 为什么加入松弛变量

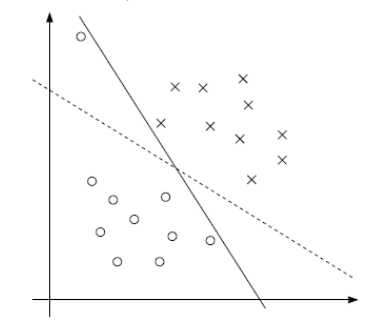
不一定完全分类正确的超平面就是最好的，如下图。用第一部分的硬间隔最大化找出的分界面很可能如实线所示，实线可以将训练数据分为两类，但其泛化能力不如虚线。

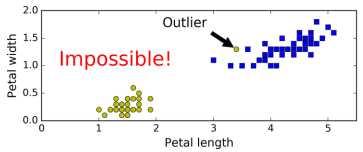
少数特异点outlier造成训练数据不是线性可分的，如下图。用第一部分的硬间隔最大化不能找出一个分界面。如果能忽视outlier，就能较好分类。

上面两张图反映了硬间隔最大化存在一些问题，所以为每个样本点引入一个松弛变量，硬间隔修改为软间隔，这就是线性不可分的支持向量机。

2 目标函数和约束

\[ \begin{aligned} \min \limits_{w,b, \xi} \quad \frac{1}{2}\|w\|^2 & +C \sum_{i=1}^{N} \xi_i\s.t. \qquad {y_i(wx_i+b) + \xi_i} & \geq 1, \quad i=1,2,\cdots,N\\xi_i & \geq 0, \quad i=1,2,\cdots,N\\end{aligned} \]
约束条件：为每个样本点引入一个松弛变量\(\xi_i \geq 0\)使得函数间隔加上松弛\(\xi_i\)不小于1。如果样本点的函数间隔本身大于1，那么\(\xi_i=0\); 如果样本点的函数间隔<1，那么\(\xi_i=1-y_i(wx_i+b)>0\)。

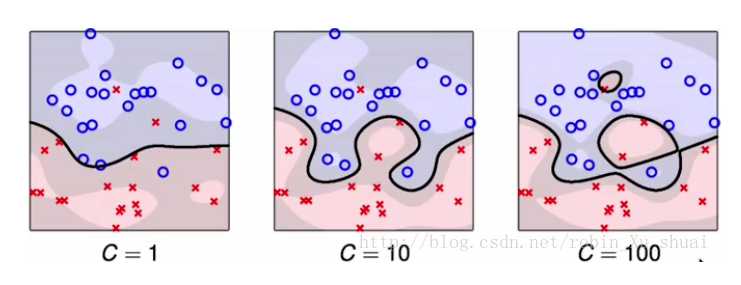
目标函数：\(\sum_{i=1}^{N} \xi_i\)代表误差，误差越小越好；\(\|w\|\)和间隔有关，\(\|w\|\)越小，间隔越宽。C是超参数，用来调节两者关系；C取得越大，对误分类的惩罚越大，当C趋于无穷大，目标函数就退化为第一部分的硬间隔最大化的目标函数；一般C取得小一些，允许训练集的少数点被分类错，从而可以达到比较好的泛化能力。

3 拉格朗日乘子法求解

3.1 构造拉格朗日函数：
\[ L(w,b,\xi,\alpha,\mu)= \frac{1}{2}\|w\|^2 +C \sum_{i=1}^{N} \xi_i-\sum_{i=1}^{N}\alpha_i[y_i(wx_i+b)+\xi_i -1]-\sum_{i=1}^{N}\mu_i\xi_i \]
其中\(\alpha = (\alpha_1,\alpha_2,\cdots,\alpha_N)^T\)是拉格朗日乘子，\(\alpha_i \geq 0\); \(\mu = (\mu_1, \mu_2, \cdots, \mu_N)^T\)也是拉格朗日乘子，\(\mu_i \geq 0\)。
3.2 把w,b,\(\xi\)看作常数，构造一个函数 \(\theta\) 定义为\(L(w,b,\xi,\alpha,\mu)\)关于\(\alpha, \mu\)求最大值
\[ \theta = \max \limits_{\alpha,\mu} L(w,b,\xi,\alpha,\mu)=\frac{1}{2}\|w\|^2+C \sum_{i=1}^{N} \xi_i \]

3.3 原始问题 $ \quad \min \limits_{w,b} \frac{1}{2}|w|^2 +C \sum_{i=1}^{N}\xi_i \quad$等价于 $ \quad \min \limits_{w,b,\xi} \max \limits_{\alpha,\mu} L(w,b,\xi,\alpha,\mu) \quad$。
根据拉格朗日对偶性，问题可变为 $ \quad \max \limits_{\alpha,\mu} \min \limits_{w,b,\xi} L(w,b,\xi,\alpha,\mu) \quad$

(1) 求\(\min \limits_{w,b,\xi} L(w,b,\xi,\alpha,\mu) \quad\)
对w,b,\(\xi_i\)分别求偏导数：
\[ \begin{aligned} \frac{\partial L}{\partial w} &= w - \sum_{i=1}^{N}\alpha_i y_i x_i\\frac{\partial L}{\partial b} &= -\sum_{i=1}^{N}\alpha_i y_i\\frac{\partial L}{\partial \xi_i} &= C-\alpha_i - \mu_i \end{aligned} \]
\(\qquad\)令偏导数=0得到：
\[ \begin{aligned} &w = \sum_{i=1}^{N}\alpha_i y_i x_i\&\sum_{i=1}^{N}\alpha_i y_i = 0\&C-\alpha_i - \mu_i = 0\\end{aligned} \]
\(\qquad\)将这三个式子带回拉格朗日函数\(L(w,b,\xi,\alpha,\mu)\)得到：
\[ L(w,b,\xi,\alpha,\mu)= -\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) + \sum_{i=1}^{N} \alpha_i \]

(2) 求 \(\min \limits_{w,b,\xi} L(w,b,\xi,\alpha,\mu)\) 对 \(\alpha,\mu\) 的极大，\(\max \limits_{\alpha,\mu} \{-\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) + \sum_{i=1}^{N} \alpha_i\}\) ,加负号得到：
\[ \begin{aligned} \min \limits_{\alpha,\mu} & {\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^{N} \alpha_i}\s.t. \qquad & \sum_{i=1}^{N} {\alpha_i y_i}=0\&C-\alpha_i - \mu_i =0 \& \alpha_i \geq 0,\& i=1,2,\cdots,N. \end{aligned} \]
消去\(\mu_i\),从而只剩下 \(\alpha_i\)，得到:
\[ \begin{aligned} \min \limits_{\alpha} &{\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N} \alpha_i\alpha_j y_i y_j (x_i x_j) - \sum_{i=1}^{N} \alpha_i}\s.t. \qquad &\sum_{i=1}^{N} {\alpha_i y_i}=0\&0 \leq \alpha_i \leq C,\&i=1,2,\cdots, N. \end{aligned} \]

(3) 假设求出了(2)中 \(\alpha\) 的最优解 \(\alpha^* =(\alpha_1^*,\alpha_2^*,\cdots,\alpha_N^*)^T\)
\(w\) 的解为 \(w^*=\sum_{i=1}^{N} \alpha_i^* y_i x_i\)
选择 $ \alpha_i^* $ 的一个正分量 $ 0<\alpha_i^*<C $ , b的解为 \(b*=y_j -w^*x_j=y_j - \sum \alpha_i^* y_i (x_i x_j)\)

4 支持向量物理意义

支持向量物理意义:
在线性不可分的情况下，支持向量不仅包括落在间隔边界上的样本点，还包括落在间隔带内的样本点以及误分类的点。落在间隔边界的点，\(\xi_i=0,\alpha_i<C\) .落在间隔带内的点或者误分类的点，\(\xi_i>0,\alpha_i=C\).
---
参数C和\(\gamma\)的影响直观理解：
http://blog.csdn.net/robin_xu_shuai/article/details/77051258
C越大，对错误分类的惩罚越大，容忍越小。

三、非线性的支持向量机

常用核函数：
多项式核函数
高斯核函数