Preface

　　对于形如给定一些边，其边权为x_i和y_i，构造一个生成树，使得

　　我们称这棵树，为最小乘积生成树。我们可以考虑，沿用最小生成树的思想，把这种新颖的最小生成树做对。

Content

算法简介

　　其实就是利用树形结合的思想，将点弄到平面直角坐标系上，使之明了，转化问题，求出最优解。

算法应用

　　应对类似的裸题，直接裸奔

算法核心

　　我们将sigma(x_i)看成横坐标，sigma(y_i)看成纵坐标，在坐标系中绘制出来。并在x,y轴作垂线，构成一个正方形

　　我们要求一种方案xy=k最小，也就是这个正方形最小，也就是反比例函数（等面积线）y=k/x最接近坐标轴（k最小，即y最小）

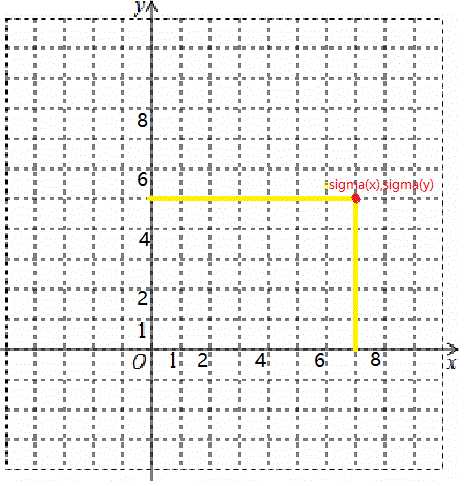
　　显然可以知道，把所有点列出来，构建一个下凸壳，最优的点(x,y)必定在下凸壳上。

　　如下图，如果一个点不在凸包上，那么以这个点作矩阵，显然面积比以被圈圈起来的点作矩阵优，这更显然吧？

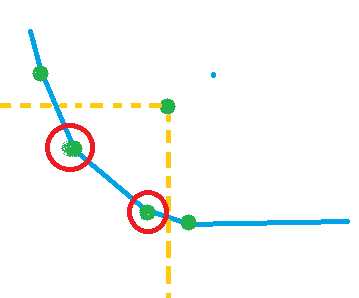
　　网上大都用分治求解

　　固定凸包上最接近x轴与y轴的两个节点，即求离x轴，y轴最近的点（分别以x，y为关键字作最小生成树即可，所得x，y必定最小）。

　　寻找一个点C，使得C离AB最远，也就是△ABC面积最大，想要用C来更新答案。这个点C是目前最优的。

　　如何找点C？我们用向量来考虑。可能觉得比较奇妙，说不出个之所以然，但是过程严谨，是没有错的，多悟一下，睡前想一想，第二天就懂了。

　　向量AB=（B.x-A.x，B.y-A.y）

　　向量AC=（C.x-A.x，C.y-A.y）

　　根据向量定义，得出S△ABC=AB